(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
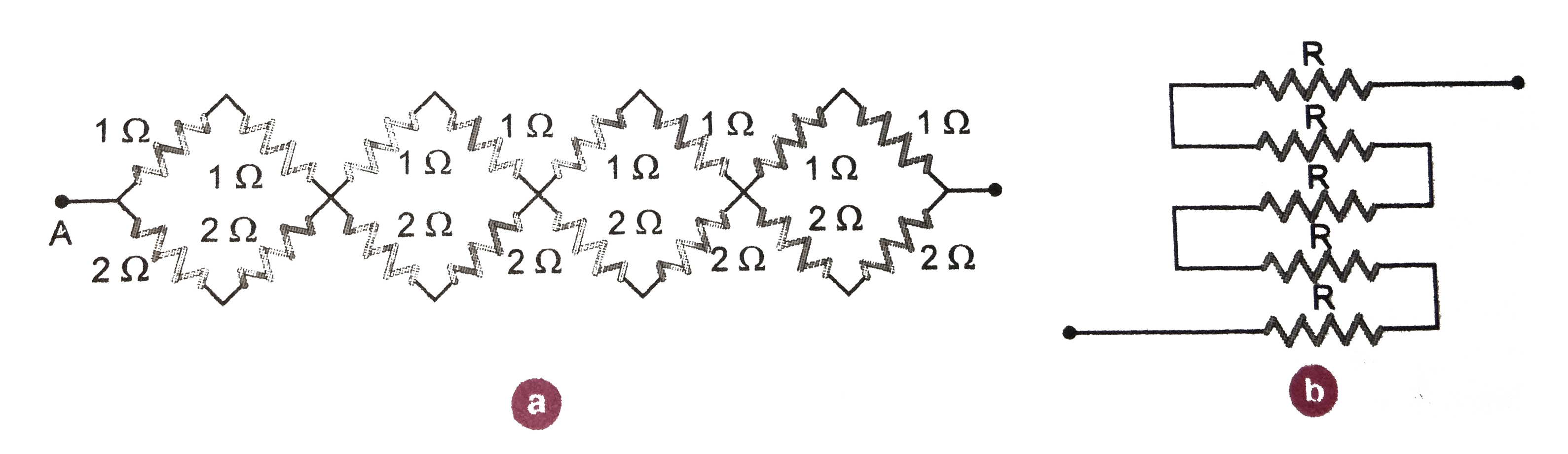
(a) For maximum effective resistance, the n resistors must be connected in series.
Maximum effective resistance, in Rs=nR.
For minimum effective resistance the n resistors must be connected in parallel.
Maximum effective resistance, Rp=R/n∴RsRp=nRR/n=n2
(b) It is to be noted that (a) the effective resistance of parallel combination of resistors is less than the individual resistance and (b) the effective resistance of series combination of resistors is more than individual resistance.
Case (i) Parallel combination of 1Ω and 2Ω is connected in series with 3Ω.
Effective resistance of 1Ω and 2Ω in parallel will be given by Rp=1×21+2=23Ω
∴ Equivalent resistance of 23Ω and 2Ω in series =23+3=113Ω
Case (ii) Parallel combination of 2Ω and 3Ω in parallel =2×32+3=65Ω
Equivalent resistance of 65Ω and 1Ω in series =65+1=115Ω
Case (iii) All the resistance are to be connected in series. Now
∴ Equivalent resistance (R) is given by 1R=11+12+13=6+3+26=116orR=611Ω
(c) The given net work is a series combination of 4 equal units. Each unit has 4 resistances in which, two resistance (1Ω each in series) are in parallel with two other resistances (2Ω each in series).
.: Effective resistance of two resistance (each of 1Ω) in series =1+1=2Ω
Effective resistance of two resistances (each of 2Ω) in series =2+2=4Ω
If Rp is the resistance of one unit of resistances, then 1Rp=12+14=34orRp=43Ω
∴ Total resistance of net work (4 such units) =43×4=164Ω=5.33Ω
For Figure. 2(NCT).2(b),the five resistance each of value R, are connected in series.
Their effective resistance =5R
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Conceptual Problems
3 Videos
- CURRENT ELECTRICITYBOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Very short Q/A
7 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise
191 Videos
Similar Questions
Given n resistors each of resistance R, how will you combine them to get the (i) maximum, and (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
View SolutionGiven n resistors each of resistane R, how will you combine them to get the (i) maximum, (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View Solution
Knowledge Check
If you are provided three resistance 2Ω,3Ω and 6Ω. How will you connect them so as to obtain the equivalent resistance of 4Ω
A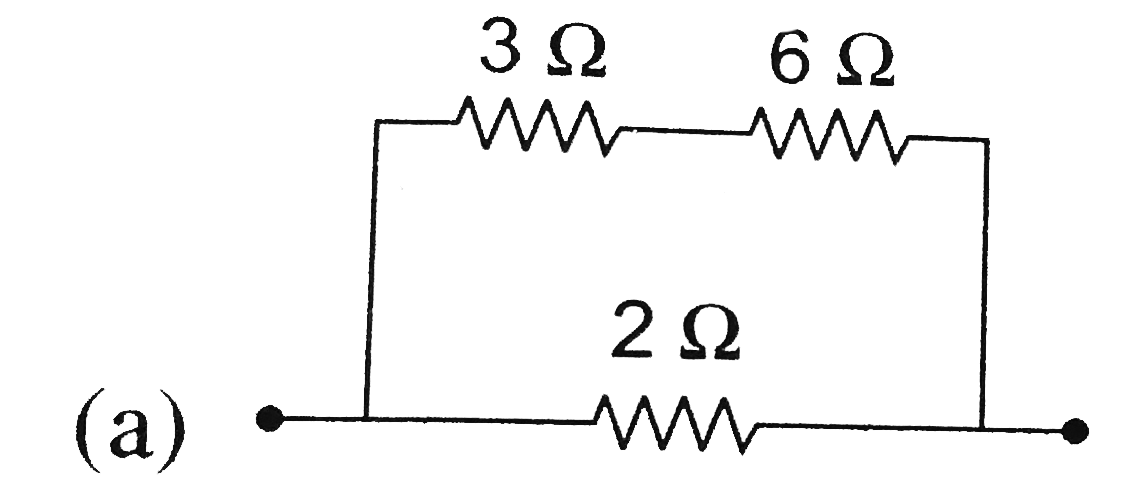 B
B C
C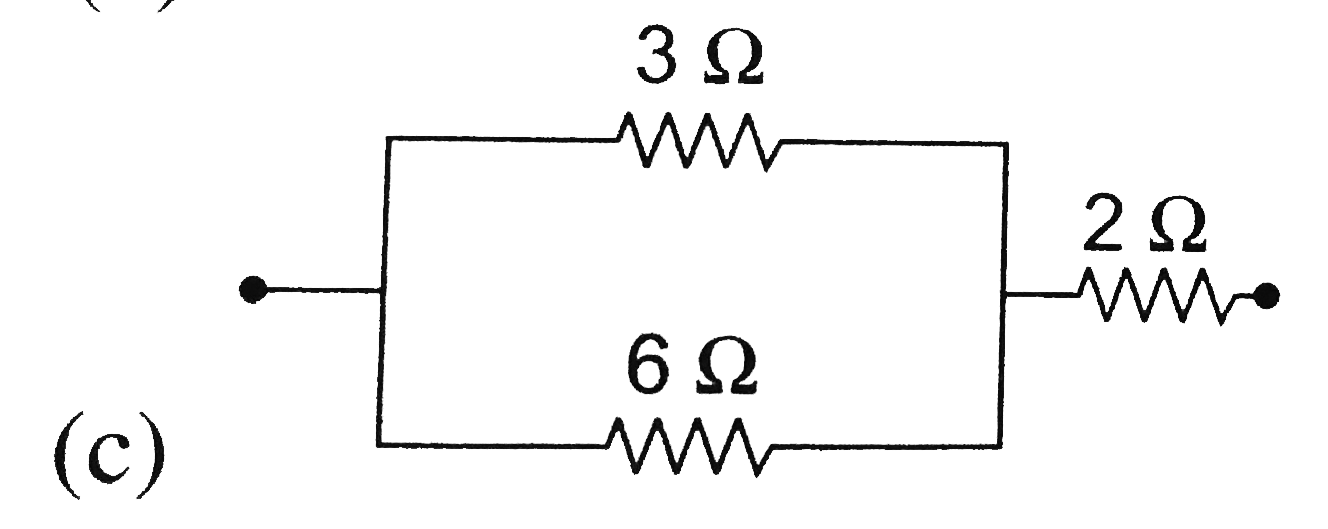 Dnone
DnoneIf you are provided three resistances 2Ω,3Ω and 6Ω. How will you connect then so as to obtain the equivalent resistance of 4Ω ?
A B
B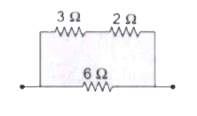 C
C Dnone of these
Dnone of these
Given the resistances of 1Ω,2Ωand3Ω. How will you combine them to get an equivalent resistance of
(i) 113Ω ?
(ii) 115Ω ?
View SolutionGiven the resistances of 1Ω,2Ω,3Ω how will we combine them to get an equivalent resistance of (i) (113)Ω,(ii)(115)Ω,(iii)6Ω,(iv)(611)Ω ?
View SolutionGiven the resistance of 1Ω,2Ω,3Ω, how will you combine them to get an e3quivalent resistance of :
113Ω (ii)115Ω (iii)6Ω 611Ω ?
View SolutionGiven three resistors of resistances 1Ω,2Ωand3Ω. How will you combine them to get an equivalent resistance of 115Ω ?
View SolutionHow can the resistances of 2Ω,3Ω and 6Ω be connected to give an effective resistance of 4Ω ?
View SolutionHow will you join the resistors of resistances 3Ω,6Ω and 8Ω to get an equivalent resistance of 10Ω?
View Solution