Given that P+Q+R= 0. Two out of the three vectors are equal in magnitude. The magnitude fo the third vector is s √2 times that of the other two. Which of the following can be the angles between these vectors?
90∘
45∘,45∘,90∘
30∘,60∘,90∘
45∘,90∘,135∘
The correct Answer is:A
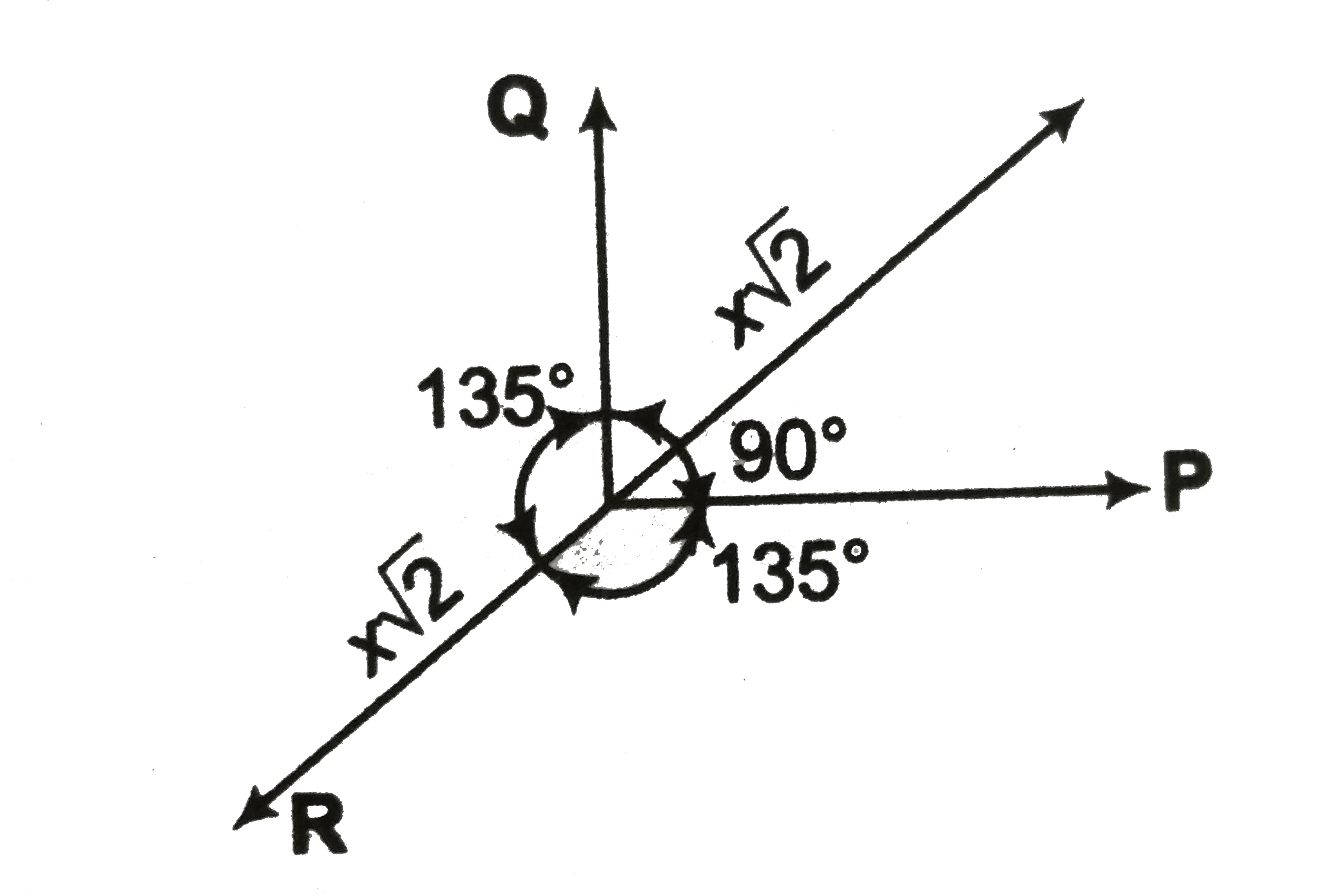
|P| = |Q| =x
|R|=√2x
Topper's Solved these Questions
- VECTORSBOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Subjective
24 Videos
- VECTORSBOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Example
39 Videos
- VECTORSBOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Exercise 5.3
4 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEYCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery
32 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
Similar Questions
Given that →A+→B+→C=→0. Out of three vectors,two are equal in magnitude and the magnitude of the third vectors is √2 times that of either of the two having equal magnitude. Find the angles between the vectors.
View SolutionGiven: →a+→b+→c=0. Out off three vectors →a,→band→c two are equal in magnitude. The magnitude of third vector is √2 times that of either of the two having equal magnitude. The angle between vectors is
View Solution
Knowledge Check
given that →A+→B+→C=0 out of three vectors two are equal in magnitude and the magnitude of third vector is √2 times that of either of the two having equal magnitude. Then the angles between vectors are given by
A30∘,60∘,90∘B40∘,45∘,90^@C45∘,60∘,90∘D90∘,135∘,135∘Given that →A+→B+→C=0, out of three vectors two are equal in magnitude and the magnitude of third vector is √2 times that of either of two having equal magnitude. Then angle between vectors are given by
A30∘,60∘,90∘B45∘,135∘,150∘C90∘,135∘,150∘D90∘,135∘,135∘Resultant of two vector of equal magnitude A is
A√3Aat60∘B√2Aat90∘C2Aat120∘DAat180∘
There vectors →P,→Qand→R are such that →P+→Q+→R=0 Vectors →P and →Q are equal in , magnitude . The magnitude of vector →R is √2 times the magnitude of either →Por→Q . Calculate the angle between these vectors .
View SolutionCalculate the angle between two vectors having magnitudes 3 and 4. The magnitude of their dot product is 2√2.
View SolutionIf the magnitude of sum of two vectors is equal to the magnitude of difference of the two vectors, the angle between these vectors is
View SolutionIf the magnitudes of two vectors are 2and3 and the magnitude of their scalar product is 3√2, then find the angle between the vectors.
View SolutionIf the magnitude of sum of two vectors is equal to the magnitude of difference of the two vectors, the angle between these vectors is
View Solution
