Which of the sets given below may represent the magnitudes of three vectors adding to zero?
2,4,8
4,8,16
1,2,1
0.5, 1.2
The correct Answer is:C
A + B + C =0
⇒C=−(A+B)
or |C|=∣−A+B)∣
or A~B≤C≤A+B.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Subjective24videos
VECTORS
- BOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Example39videos
VECTORS
- BOOK - DC PANDEYCHAPTER - VECTORSEXERCISE - Exercise 5.34videos
VECTORS
- BOOK - DC PANDEYCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery32videos
UNITS, DIMENSIONS & ERROR ANALYSIS
- BOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question11videos
WAVE MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
The circuit given below represents which of the logic operations ?
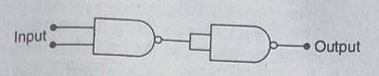 AANDBNOTCORDNOR
AANDBNOTCORDNOR - Question 2 - Select One
The circuit given below represents which of the logic operations ?
 AANDBNOTCORDNOR
AANDBNOTCORDNOR - Question 3 - Select One
The circuit given below represents which of the logic operations?
 ANOTBANDCORDNOR
ANOTBANDCORDNOR
There is a set of elements: Cooler, Television, Electronic gadgets. Which figure given below will best represent the relationship among these three elements ?
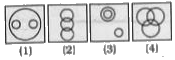 View Solution
View SolutionWhich of the following set of magnitudes of three forces can't make zero resultant (All are coplanar)
View SolutionThe x- component of the resultant of several vectors
(i) is equal to the sum of the x-components of the vectors
(ii) may be smaller than the sum of the magnitudes of the vectors
(iii) may be greater than the sum of the magnitudes of the vectors
(iv) may be equal to the sum of the magnitudes of the vectorsView SolutionAsserion: Magnitude of the resultant of two vectors may be less than the magnitude of either vector.
Reason: The resultant of two vectors is obtained by means of law of parallelogram of Vectors.View SolutionGiven that →A+→B+→C=0, out of three vectors two are equal in magnitude and the magnitude of third vector is √2 times that of either of two having equal magnitude. Then angle between vectors are given by
View Solution

