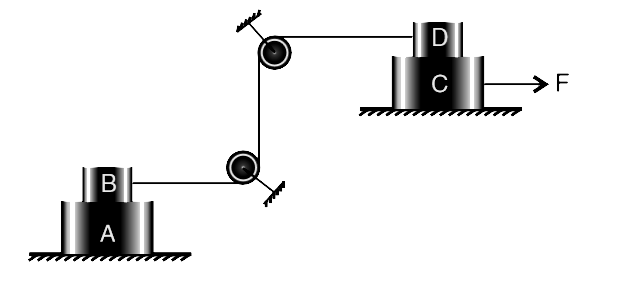
Given the setup shown in Fig Block A,B and C have masses mA=M and mB=mC=m. The strings are assumed maseless and unstreichable, and the pulleys frictionless .There is no friction between block B and the support table, but there is friction between blocks B and C, denoted by a given coefficient μ

a . In terms the given find (i) the acceleration of block A and B
b. Suppose the system is released from rest with block C near the right end of block B as shown in the above figure. If the the length L of block B is given, what is the speed of block C as it reached the left end of block B ? Tear the size of C as small
c. If the mass of block A is less then some critical value, the blocks will not accelerate when released from rest. Write down as expression for that critical mass.
a. Apply constrain on string , the length of strings is constant . Differentiate twice to get relation between acceleration .Let the acceleration of block A,B and C be a, b and c respectively
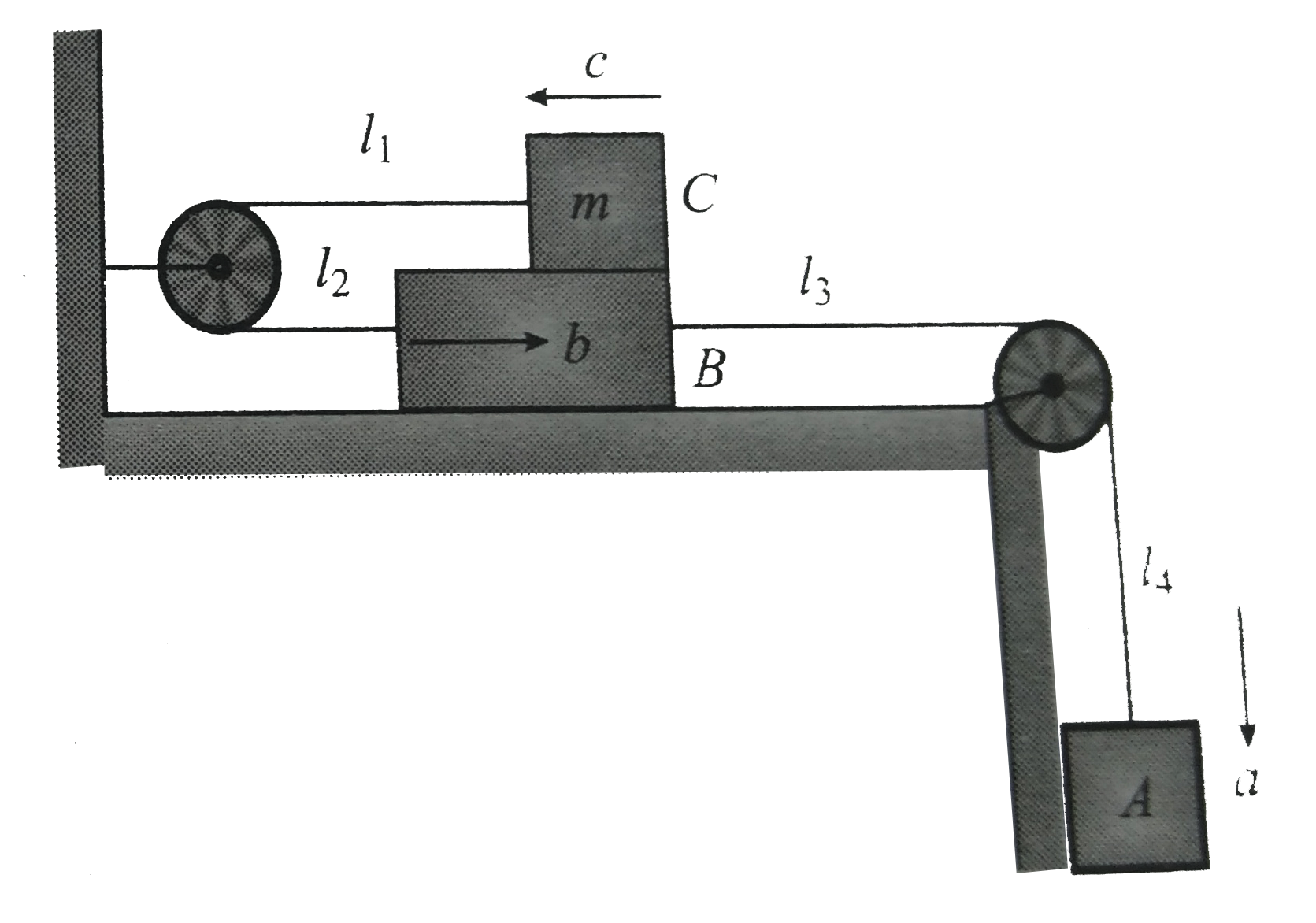
l1+l2= constant
l3+l4= constant
..l1+..l2=0⇒|b|=|c|
..l3+..l4=0⇒|a|=|b|
From which we get a=b=c
From FBD of A,B and C [Fig (a)]
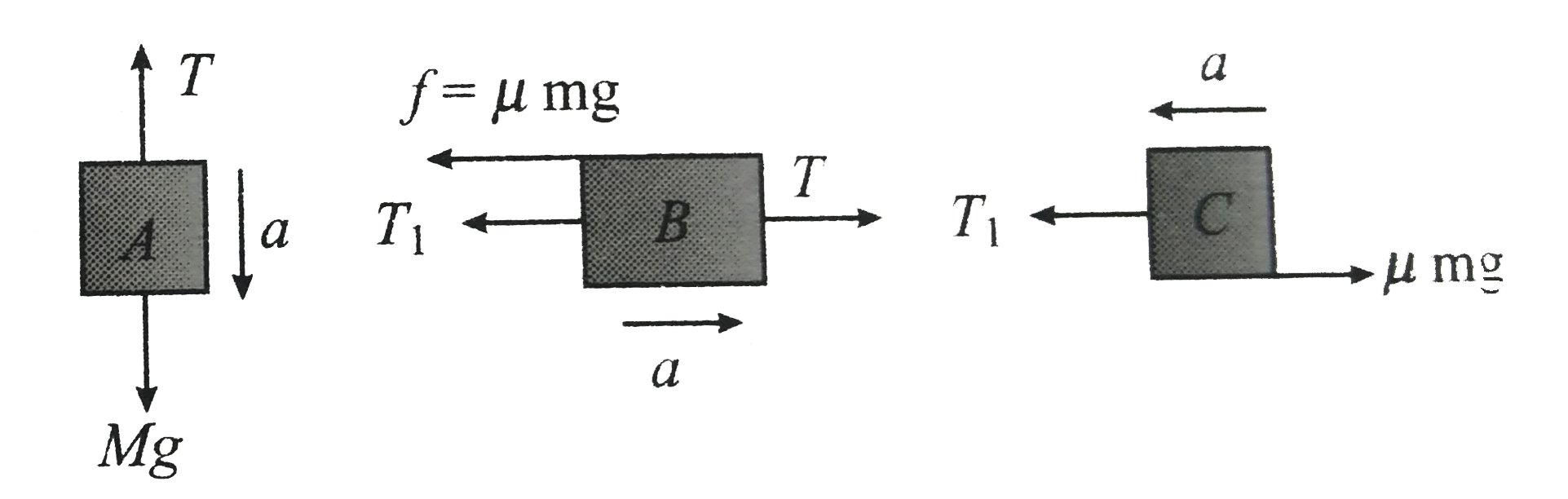
Writing equation of motion for block A :
Mg−T=Ma .....(i)
For block B,T−T1−μmg=ma .....(ii)
Solving equation (i) ,(ii) and (iii) we get
a=(M−2μmM+2m)g....(iv)
Putting a in Eq (i), we get
Mg−T=M(M−2μmM+2m)g⇒T=2mMg(1+μ)(M+2m)
b. As there is relative motion between blocks , we apply
v2rel=v2rel+2arelSrel
If system is released from rest urel=0
v2rel=2arelSrel⇒vrel=√2arelSrel
arel=2a and Srel=L
⇒v=√4gL(M−2μm)(M+2m)
cIf blocks will not acceleration , than put a=0in Eq (iv) to getM=2μm.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples12videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.125videos
NEWTON'S LAWS OF MOTION 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer5videos
NEWTON'S LAWS OF MOTION 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
Similar Questions
In the figure masses m1, m2 and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between m1 and M and that between m2 and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between P1 and m1 and also between P2 and m2. The string is perfectly vertical between P1 and P2. An external horizontal force F is applied to the mass M. Take g=10m/s2.
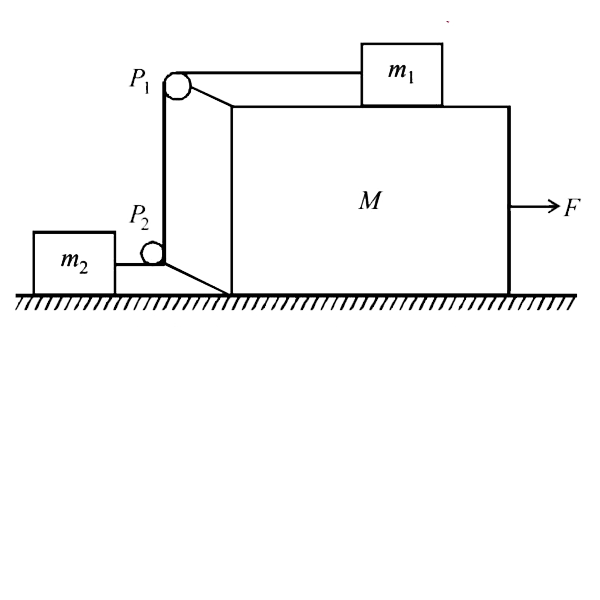
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between m1 and M be f1 and that between m2 and ground be f2. For a particular F it is found that f1=2f2. Find f1 and f2. Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.10:25View SolutionA block weighing 20N rests on a horizontal surface . The coefficient of static friction between the block and surface is 0.4 and the coeffiecient of kinetic frictioni 0.20
a.How much is the friction force excerted on the block?
b. How much will the friction force be if a horizontal force of 5N is exerted on the block?
c. What is the minimum force that will start the block in motion ?
d. What is the minimum force that will keep the block in motion once is has been started ?
e. If the horizontal force is 10N what is the friction force?02:10View SolutionA block is placed on an inclined plane moving towards right horizontally with an acceleration a0=g. The length of the plane AC=1m. Friction is absent everywhere. Find the time taken (in seconds) by the block to reach from C to A.
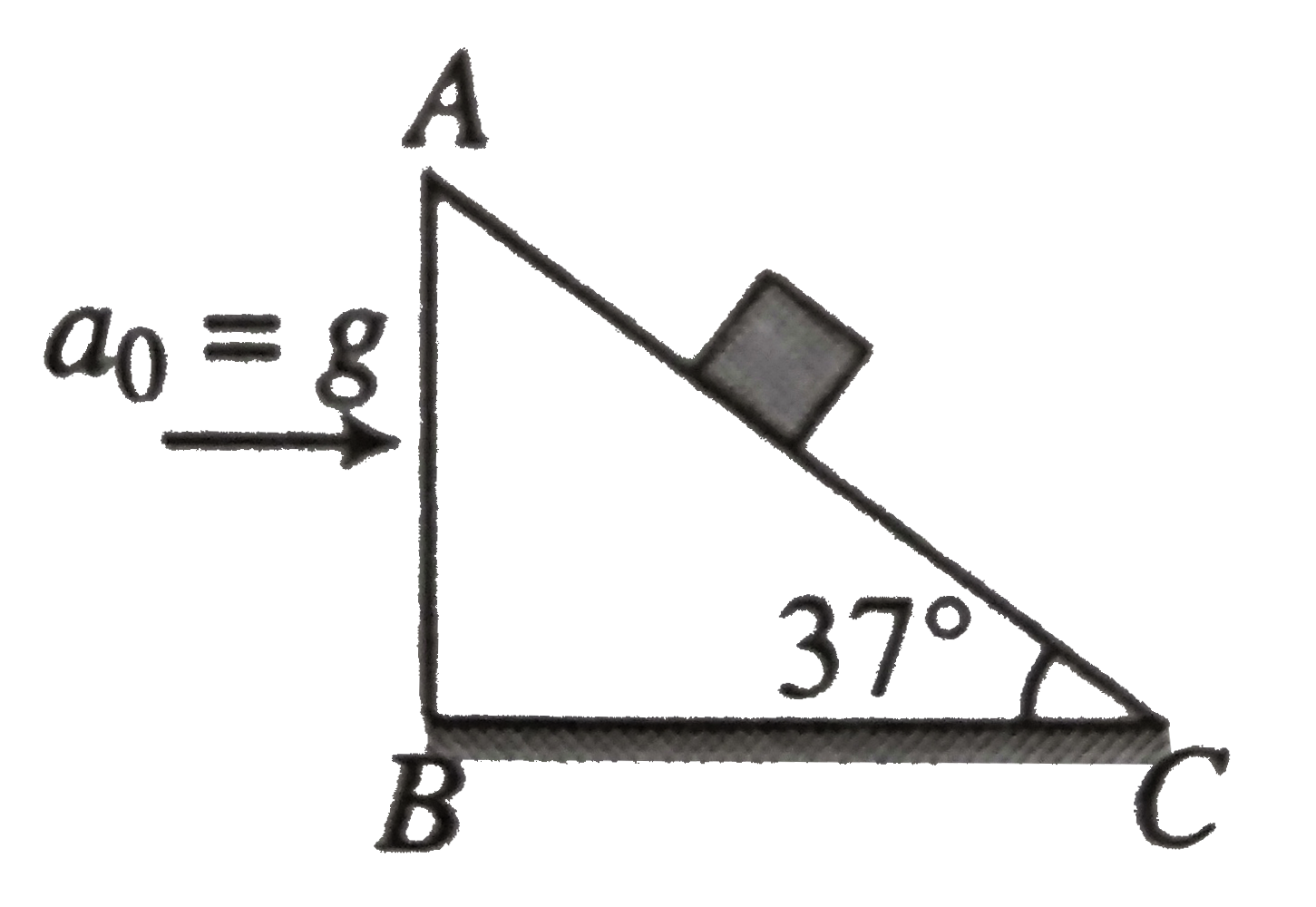 01:27View Solution
01:27View SolutionTwo soap bubbles A and B are kept in aclosed chamber where the air is maintained at pressure 8Nm2. The radiiof bubbles A and B are 2cm and 4 cm , respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. The ratio of nB/nAis ( where nA and nB are the numbe of moles of air in bubbles A and B,respectively.)
[Neglect the effect of gravity]01:16View SolutionGiven the setup shown in Fig Block A, B and C have masses m_(A)= M and m_(B) =m_(C) = m . The strings are assumed maseless and unstreichable, and the pulleys frictionless .There is no friction between block B and the support table, but there is friction between blocks B and C , denoted by a given coefficient mu a . In terms the given find (i) the acceleration of block A and B b. Suppose the system is released from rest with block C near the right end of block B as shown in the above figure. If the the length L of block B is given, what is the speed of block C as it reached the left end of block B ? Tear the size of C as small c. If the mass of block A is less then some critical value, the blocks will not accelerate when released from rest. Write down as expression for that critical mass.
06:04View SolutionFind the acceleration of the two blocks The system is initaily at rest the friction coefficient are as in fig 7.138 Given m_(A) = m_(B) = 10 kg
06:18View SolutionFind the acceleration of the two blocks . The system is initialy at rest and the friction are as shown in fig .Given m_(A) = m_(B) = 10 kg
02:27View SolutionTwo blocks A and B of masses mA and mB have velocity v and 2v respectively at a given instant A horizontal force F acts on the block A There is no friction between ground and block B and coefficient of friction between A and B is μ The friction
 04:57View Solution
04:57View SolutionBlock B of mass mB=0.5kg rests on block A, with mass mA=1.5kg which in turn is on a horizontal tabletop (as shown in figure) .The coefficient of kinetic friction between block A and the tabletop is μk=0.4 and the coefficient of static friction between block A and blockB is μs=0.6 A light string attached block A passes over a frictionless, massless pulley and block C is suspended from the other end of the string. What is the largest mass mc (in kg) that block C can have so that block A and B still slide together when the system is replaced from rest?
 02:00View Solution
02:00View SolutionThe coefficient of friction between the block A of mass m & block B of mass 2m is mu . There is no friction between A & B is released from rest & there is no slipping between A & B then:
11:27View SolutionIn the system shown in fig., block A and C are placed on smooth floors and both have mass equal to m1. Blocks B and D are identical having mass m2 each. Coefficient of friction
Between A and B and that between C and D are both equal to μ. String and pulleys are light. A horizontal force F is applied on block C and is gradually increased.
(a) Find the maximum value of F (call it F0) so that all the four blocks move with same acceleration.
(b) Will the value of F0 increase or decrease if another block (E) of mass m2 is placed above block D and coefficient of friction between E and D is μ?03:16View SolutionTwo blocks A and B are connected by as string as shown in figure. Friction coefficient of the incline plane and block is 0.5 . The mass of the block A is 5 kg . If minimum & maximum values of masses of the block B for which the block remains in equilibrium are m_(1) & m_(2) then find value of (m_(2) - m_(1)) .
View SolutionThree blocks are placed as shown in figure. Mass of A, B and C are m_(1), m_(2),"and "m_(3) respectively. The force exerted by block 'C' on 'B' is :-
04:03View SolutionPulleys shown in the system of the figure are massless and friction less. Threads are inextensible. Mass of block A, B and C are m1kg,m2=4kg and m3=2.75kg, respectively .Calculate acceleration of A block
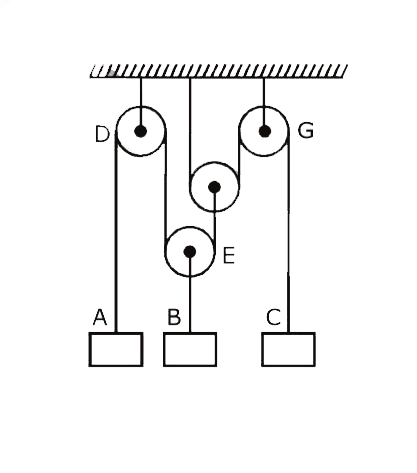 05:16View Solution
05:16View SolutionFind the relation between acceleration of the two blocks m_(1) and m_(2) . Assume pulleys are massless and frictionless and the strings are inextensible .
10:16View Solution
