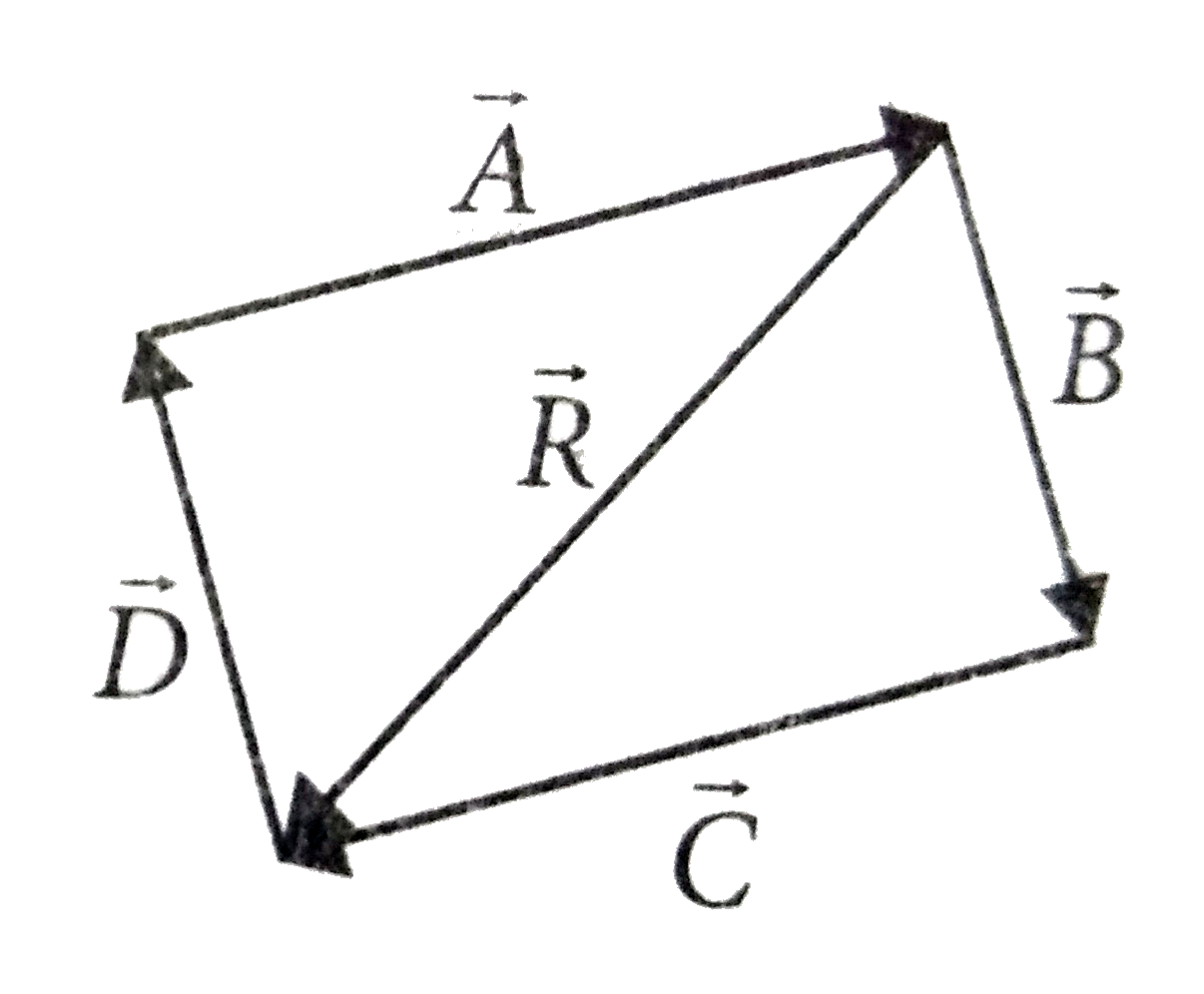
Given $\to A + \to B + \to C + \to D = \to 0$ , which of the following statements is not correct ?

$\to A, \to B, \to C and \to D$ must each be a null vector.

The magnitude of $(\to A + \to C)$ equals the magnitude of $(\to B + \to D)$ .

The magnitude of $\to A$ can never be greater than the sum of the magnitudes of $\to B, \to C and \to D .$

$\to B + \to C$ must lie in the plane of $\to A and \to D$ if $\to A and \to D$ are not collinear and in the line of $\to A and \to D$ , if they are collinear.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

The statement is not correct. It is because $\to A + \to B + \to C + \to D$ can be zero in many ways other than $\to A, \to B, \to C and \to D$ being each a rull vector.
(b) The statement is correct as proved below
$\to A + \to B + \to C + \to D = \to 0 or \to A + \to C = - (\to B + \to D)$
$∴ ∣ ∣ \to A + \to C ∣ ∣ = ∣ ∣ \to B + \to D ∣ ∣$
(c ) The statement is correct and can be proved using triangular inequality.
$∣ ∣ \to B ∣ ∣ + ∣ ∣ \to C ∣ ∣ \geq ∣ ∣ \to R ∣ ∣ ... (i)$
$∣ ∣ \to R ∣ ∣ + ∣ ∣ \to D ∣ ∣ \geq ∣ ∣ \to A ∣ ∣ ... (i i)$
Using (i) and (ii), $∣ ∣ \to A ∣ ∣ \leq ∣ ∣ \to B ∣ ∣ + ∣ ∣ \to C ∣ ∣ + ∣ ∣ \to D ∣ ∣$
(d) THe statement is correct as proved below
$\to A + \to B + \to C + \to D = \to 0 or \to A + (\to B + \to C) + \to D = \to 0$
The resultant sum of three vectors $\to A, (\to B + \to C)$ and $\to D$ can be zero only if $(\to B + \to C)$ lies in the plane of $\to A and \to D$ and these three vectors are represented by the three sides of a triangle taken in one order. IF $\to A and \to D$ are collinear, then $(\to B + \to C)$ must be in the line of $\to A and \to D$ , only then the vector sum of all the vectors will be zero.

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Let $\to a, \to b, \to c$ be unit vetors such that $\to a + \to b + \to c = \to 0$ , which one of the following is correct ?
A $\to a \times \to b = \to b \times \to c = \to c \times \to a = \to 0$
B $\to a \times \to b = \to b \times \to c = \to c \times \to a \neq \to 0$
C $\to a \times \to b = \to b \times \to c = \to a \times \to c = \to 0$
D $\to a \times \to b, \to b \times \to c, \to c \times \to a$ are mutually perpendicular vectors.
Question 2 - Select One
Two vectors $\to A$ and $\to B$ are such that $\to A + \to B = \to C$ and $A^{2} + B^{2} = C^{2}$ . Which of the following statements, is correct:-
AA is parallel to B
BA is antiparallel to B
CA is perpendicular to B
DA and B are equal in magnitude
Question 3 - Select One
If $(\to a \times v \to b) \times (\to c \times \to d) . (\to a \times \to d) = 0$ then which of the following may be true ?
A $\to a, \to b and \to d$ are nenessarily coplanar
B $\to a$ lies iin the plane of $\to c and \to d$
C $\to v b$ lies in the plane of $\to a and \to d$
D $\to c$ lies in the plane of $\to a and \to d$

NCERT FINGERTIPS-MOTION IN A PLANE -Addition And Subtraction Of Vectors - Graphical Method

Home
Ask Doubt
Profile

Given →A+→B+→C+→D=→0, which of the following statements is not correct ?

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let →a,→b,→c be unit vetors such that →a+→b+→c=→0 , which one of the following is correct ?

Two vectors →A and →B are such that →A+→B=→C and A2+B2=C2. Which of the following statements, is correct:-

If (→a×v→b)×(→c×→d).(→a×→d)=0 then which of the following may be true ?

NCERT FINGERTIPS-MOTION IN A PLANE -Addition And Subtraction Of Vectors - Graphical Method

Given $\to A + \to B + \to C + \to D = \to 0$ , which of the following statements is not correct ?

Let $\to a, \to b, \to c$ be unit vetors such that $\to a + \to b + \to c = \to 0$ , which one of the following is correct ?

Two vectors $\to A$ and $\to B$ are such that $\to A + \to B = \to C$ and $A^{2} + B^{2} = C^{2}$ . Which of the following statements, is correct:-

If $(\to a \times v \to b) \times (\to c \times \to d) . (\to a \times \to d) = 0$ then which of the following may be true ?