Here we calculate on instantaneous work - that is, the rate at which work is being done at any given instant rather than averaged over a time interval. Figure 8-34 shows constant forces →F1 and →F2 acting on a box as the box slides rightward across a frictionless floor. Force →F1 is horizontal , with magnitude 2.0 N, force →F2 is angled upward by 60∘ to the floor and has magnitude 4.0 N. The speed v of the box at a certain instant is 3.0 m/s. What is the power due to each force acting on the box at that instant, and what is the net power? Is the net power changing at that instant?
KEY IDEAS
We want an instantaneous power, not an average power over a time period. Also, we know the box.s velocity (rather than the work done on it).
Calculation: We use Eq. 8-87 for each force, For force →F1 at angle ϕ1=180∘ to velocity →v , we have
P1=F1vcosϕ1=(2.0N)(3.0m/s)cos180∘
=−6.0 W.
This negative result tells us that force →F1 is transferring energy from the box at the rate of 6.0 J/s.
For force →F2, at angle ϕ2=60∘ to velocity →v, we have
P2=F2vcosϕ2=(4.0N)(3.0m/s)cos60∘
=6.0W.
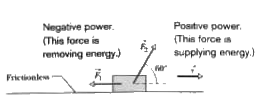
Figure 8-34 Two forces →F1 and →F2 act on a box that slides reightward across a frictionless floor. The velocity of the box is →v.
This positive result tells us that force →F2 is transferring energy to the box at the rate of 6.0 J/s.
The net power is the sum of the individual powers ( complete with their algebraic signs):
Pnet=P1+P2
=−60W+6.0W=0,
Which tells us that the net rate of transfer of energy to or from the box is zero. Thus, the kinetic energy (K=1/2mv2) of the box is not changing, and so the speed of the box will remain at 3.0 m//s. With neither the forces →F1 and →F2 nor hte velocity →v changing , We see from Eq. 8-88 that P1 and P2 are constant and thus So is Pnet.
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PROBLEMS
58 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A smooth track is in the form of a quarter circle of radius 10 m lies in the vertical plane. A bead moves from A and B along the circular track under the action of forces →F1,→F2 and →F3 Force →F1 acts always towards point B and is always 20 N in magnitude Force →F2 always acts horizontally and is always 25 N in magnitude. Force →F3 always acts tangentially to the track and is of constant magnitude 10 N. Select the correct answer.

View SolutionWhich of the figure's six arrangements correctly show the vector addition of forces →F1 and →F2 to yield the third vector, which is meant to represent their net force →Fnet ?

View Solution
Knowledge Check
Two forces −→F1and−→F2 are acting at right angles to each other , find their resultant ?
A√F21−F22B√F21+F22C√(F1+F2)DF1+F2Two constant forces →F1 and →F2 acts on a body of mass 8 kg. These forces displaces the body from point P(1,−2,3) to Q(2,3,7) in 2s starting from rest. Force →F1 is of magnitude 9 N and is acting along vector (2ˆi−2ˆj+ˆk) . Work done by the force →F2 is :-
A80JB−80JC−180JD180JA body of mass m has an initial speed v is acted by two forces →F1 and →F2. After something work done by →F1 is −12mv2 and speed of the body is 2v. Then, the work done by →F2 is
A32mv2Bmv2CzeroD2mv2
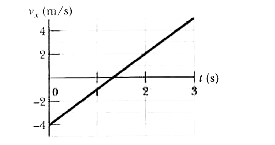
Two horizontal forces →F1 and →F2 act on a 4.0 kg disk that slides over frictionless ice, on which an xy coordinate system over frictionless ice, on which an xy coordinate system is laid out. Force →F1 is in the positive direction of the x axis and has a magnitude of 7.0 N. Force →F2 has a magnitude of 9.0 N. Figure 5-39 gives the x component vx of the velocity of the disk as a function of time t during the sliding. What is the angle between the constant directions of forces →F1 and →F2 ?
View SolutionWhen force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
View SolutionA smooth track is in the form of a quarter circle of radius 10 m lies in the vertical plane. A bead moves from A and B along the circular track under the action of forces →F1,→F2 and →F3 Force →F1 acts always towards point B and is always 20 N in magnitude Force →F2 always acts horizontally and is always 25 N in magnitude. Force →F3 always acts tangentially to the track and is of constant magnitude 10 N. Select the correct answer.

View SolutionIf →F is the force acting in a particle having position vector →r and →τ be the torque of this force about the origin, then
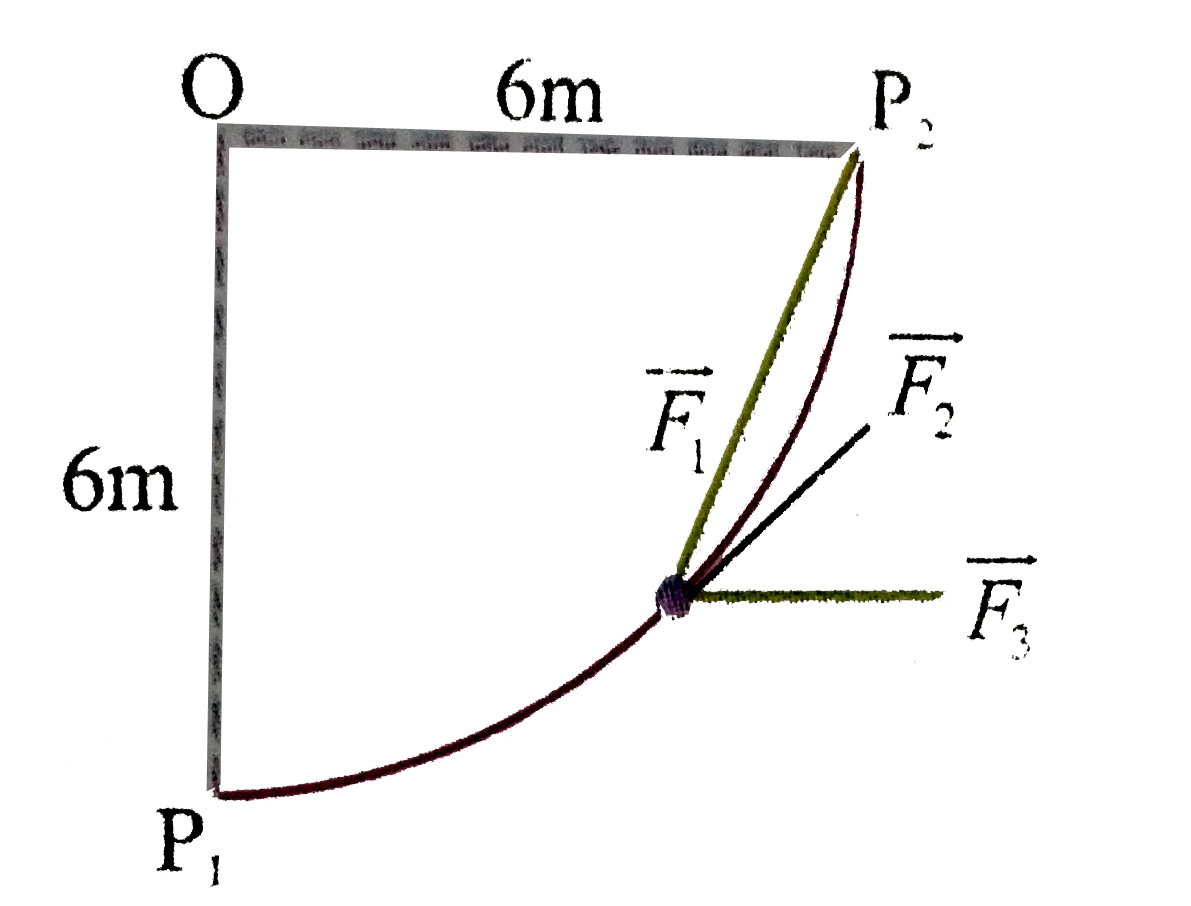
View SolutionA smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is 20N, Force →F2 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
 .
.
View Solution
