Holding on to a tow rope moving parallel to a frictionless ski slope, a 45 kg skier is pulled up the slope, which is at an angle of 8.0∘ with the horizontal. What is the magnitude Frope of the force on the skier from the rope when (a) the magnitude v of the skier's velocity is constant at 2.0 m/s and (b) v = 2.0 m/s as v increases at a rate of 0.10 m/s2 ?
To solve the problem step by step, let's break it down into two parts as given in the question.
Given Data:
- Mass of the skier, m=45kg
- Angle of the slope, θ=8∘
- Gravitational acceleration, g=9.8m/s2
Part (a): When the skier's velocity is constant at 2.0m/s
1. Identify Forces Acting on the Skier:
- The weight of the skier acts downward, which can be decomposed into two components:
- Perpendicular to the slope: mgcosθ
- Parallel to the slope: mgsinθ
2. Since the skier is moving at constant velocity:
- The acceleration a=0
- According to Newton's first law, the net force acting on the skier must be zero.
3. Set Up the Equation:
- The force exerted by the rope Frope must balance the component of the weight acting down the slope:
Frope−mgsinθ=0
- Therefore, we have:
Frope=mgsinθ
4. Calculate mgsinθ:
- First, calculate mg:
mg=45kg×9.8m/s2=441N
- Now calculate sin(8∘):
sin(8∘)≈0.1392
- Now plug in the values:
Frope=441N×0.1392≈61.54N
5. Final Result for Part (a):
Frope≈61.54N
Part (b): When the skier's velocity is 2.0m/s and accelerating at 0.10m/s2
1. Identify Forces Acting on the Skier:
- The same forces are acting as in part (a).
2. Since the skier is accelerating:
- The net force acting on the skier is given by Newton's second law:
Fnet=ma
- Here, a=0.10m/s2.
3. Set Up the Equation:
- The equation now becomes:
Frope−mgsinθ=ma
- Rearranging gives:
Frope=ma+mgsinθ
4. Calculate ma and mgsinθ:
- Calculate ma:
ma=45kg×0.10m/s2=4.5N
- We already calculated mgsinθ in part (a) as approximately 61.54N.
5. Final Calculation for Part (b):
Frope=4.5N+61.54N≈66.04N
Final Results:
- (a) Frope≈61.54N
- (b) Frope≈66.04N
---
- Mass of the skier, m=45kg
- Angle of the slope, θ=8∘
- Gravitational acceleration, g=9.8m/s2
- The weight of the skier acts downward, which can be decomposed into two components:
- Perpendicular to the slope: mgcosθ
- Parallel to the slope: mgsinθ
- The acceleration a=0
- According to Newton's first law, the net force acting on the skier must be zero.
- The force exerted by the rope Frope must balance the component of the weight acting down the slope:
Frope−mgsinθ=0
- Therefore, we have:
Frope=mgsinθ
- First, calculate mg:
mg=45kg×9.8m/s2=441N
- Now calculate sin(8∘):
sin(8∘)≈0.1392
- Now plug in the values:
Frope=441N×0.1392≈61.54N
Frope≈61.54N
- The same forces are acting as in part (a).
- The net force acting on the skier is given by Newton's second law:
Fnet=ma
- Here, a=0.10m/s2.
- The equation now becomes:
Frope−mgsinθ=ma
- Rearranging gives:
Frope=ma+mgsinθ
- Calculate ma:
ma=45kg×0.10m/s2=4.5N
- We already calculated mgsinθ in part (a) as approximately 61.54N.
Frope=4.5N+61.54N≈66.04N
- (a) Frope≈61.54N
- (b) Frope≈66.04N
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)36videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)5videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT5videos
FORCE AND MOTION - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )5videos
FLUIDS
- BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)1videos
FORCE AND MOTION-II
Similar Questions
A 50 kg skier skis directly down a frictionless slope angled at 10∘ to the horizontal. Assume the skier moves in the negative direction of an x axis along the slope. A wind force with component Fx acts on the skier. What is Fx if the magnitude of the skier's velocity is (a) constant, (b) increasing at a rate of 1.0 m/s2, and (c) increasing at a rate of 2.0 m/s2 ?
View SolutionWhat kind of energy does the skier have at the top of the slope?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Figure shows a heavy block kept on a frictionless surface and being pulled on the left rope is withdrawn but the force on the right end continues to act. Let F1 and F_2 be the magnitude of the forces by the right rope and the left rope on the block respectively.
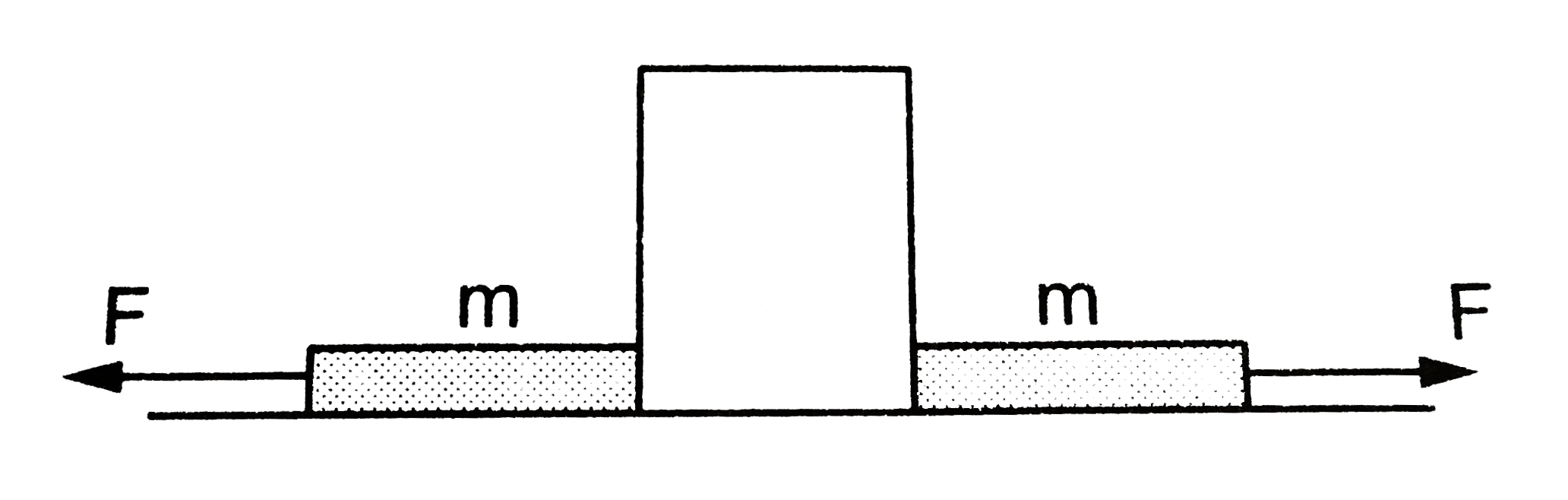 AF1=F2=Ffort<0BF1=F2=F+mgfort<0CF1=F,F2=Ffort<0DF1<F,F2=Ffort>0
AF1=F2=Ffort<0BF1=F2=F+mgfort<0CF1=F,F2=Ffort<0DF1<F,F2=Ffort>0 - Question 2 - Select One
In the block moves up with constant velocity v m//s. Find F
 AF=mg2BF=2mg3CF=mg3DF=m3
AF=mg2BF=2mg3CF=mg3DF=m3 - Question 3 - Select One
What is the magnitude of the average acceleration of a skier who, starting from rest, reaches a speed of 8.0 m/s when going down a slope for 5.0 s ?
A0.85m/s2B1.1m/s2C1.6m/s2D1.9m/s2
What happens to that energy after the skier races down the slope of the mountain?
 View Solution
View SolutionA skier is pulled by towrope up frictionless ski slope that makes an angle of 12∘ with the horizontal . The rope moves parallel to the slope with a constant speed of 1.0 m/s. The force of the rope does 880 J of work on the skier as the skier moves a distance of 7.0 m up the incline. (a) If the rope moved with a constant speed of 2.0 m/s, how much work would the force of the rope do on the skier as the skier moved a distance of 8.0 m up the incline ? At what rate is the force of the rope doing work on the skier when the rope moves with a speed of (b) 1.0 m/s and (c) 2.0 m/s ?
View SolutionWhile sking on snow, a skier wear skis in addition to the shoes. Why ?
View SolutionA 63-kg skier goes up a snow-convered hill that makes an angle of 25∘ with the horizontal . The initial speed of the skier is 6.6 m/s. After coasting a distance of 1.9 m up the slope, the speed of the skier is 4.4 m/s. Find the work done by the kinetic frictional force that acts on the skis .
View SolutionA block is lying on the horizontal frictionless surface. One end of a uniform rope is fixed to the block which is pulled in the horizontal direction by applying a force F at the other end. If the mass of the rope is half the mass of the block. The tension in the middle of the rope will be
View Solution

