A 93 kg man lowers himself to the grouund from a height of 10.0 m by holding onto a rope that runs over a frictionless pulley to a 65 kg sandbag. With runs over a frictionless pylley to a 65 kg sandbag. With what speed does the man hit the ground if he started from rest ?
To solve the problem of the 93 kg man lowering himself from a height of 10.0 m while connected to a 65 kg sandbag, we can follow these steps:
Step 1: Identify the Forces
- The weight of the man (W_m) is given by:
Wm=mm⋅g=93kg⋅9.81m/s2=913.53N
- The weight of the sandbag (W_s) is given by:
Ws=ms⋅g=65kg⋅9.81m/s2=637.65N
Step 2: Set Up the Equations
- The tension (T) in the rope can be expressed for the sandbag:
T=Ws=637.65N
- For the man, using Newton's second law:
Wm−T=mm⋅a
Substituting the values:
913.53−T=93⋅a
Step 3: Substitute Tension
- Substitute T from the sandbag equation into the man's equation:
913.53−637.65=93⋅a
Simplifying this gives:
275.88=93⋅a
Therefore, we can solve for acceleration (a):
a=275.8893≈2.96m/s2
Step 4: Use Kinematics to Find Final Velocity
- Since the man starts from rest (initial velocity, u = 0) and falls a distance (h = 10 m), we can use the kinematic equation:
v2=u2+2ah
Substituting the known values:
v2=0+2⋅2.96⋅10
Simplifying this gives:
v2=59.2
Taking the square root to find v:
v≈√59.2≈7.7m/s
Final Answer
The speed at which the man hits the ground is approximately 7.7 m/s.
---
- The weight of the man (W_m) is given by:
Wm=mm⋅g=93kg⋅9.81m/s2=913.53N
- The weight of the sandbag (W_s) is given by:
Ws=ms⋅g=65kg⋅9.81m/s2=637.65N
- The tension (T) in the rope can be expressed for the sandbag:
T=Ws=637.65N
- For the man, using Newton's second law:
Wm−T=mm⋅a
Substituting the values:
913.53−T=93⋅a
- Substitute T from the sandbag equation into the man's equation:
913.53−637.65=93⋅a
Simplifying this gives:
275.88=93⋅a
Therefore, we can solve for acceleration (a):
a=275.8893≈2.96m/s2
- Since the man starts from rest (initial velocity, u = 0) and falls a distance (h = 10 m), we can use the kinematic equation:
v2=u2+2ah
Substituting the known values:
v2=0+2⋅2.96⋅10
Simplifying this gives:
v2=59.2
Taking the square root to find v:
v≈√59.2≈7.7m/s
The speed at which the man hits the ground is approximately 7.7 m/s.
Topper's Solved these Questions
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
36 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)
5 Videos
- FORCE AND MOTION - I BOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION - I EXERCISE - CHECKPOINT
5 Videos
- FLUIDSBOOK - RESNICK AND HALLIDAYCHAPTER - FLUIDSEXERCISE - PRACTICE QUESTIONS (Integer Type )
5 Videos
- FORCE AND MOTION-IIBOOK - RESNICK AND HALLIDAYCHAPTER - FORCE AND MOTION-IIEXERCISE - PRACTICE QUESTIONS (Integer Type)
1 Videos
Similar Questions
A 4kg block is on a smooth horizontal table. The block is connected to a second block of mass 1kg by a massless flexible taut cord that passes over a frictionless pulley. The 1kg block is 1m above the floor. The two block are released from rest. With what speed does the 1kg block hit the ground?
 .
.
View SolutionA man of mass 50 kg starts moving on the earth and acquires speed of 1.8 m/s. with what speed does the earth recoil? Mass of earth =6×1024kg.
View Solution
Knowledge Check
A body of mass 0.1kg is suspended at a height of 1m about the ground by a weightless string which passes over a frictionless pulled, Fig. The velocity with which the body strikes the ground is
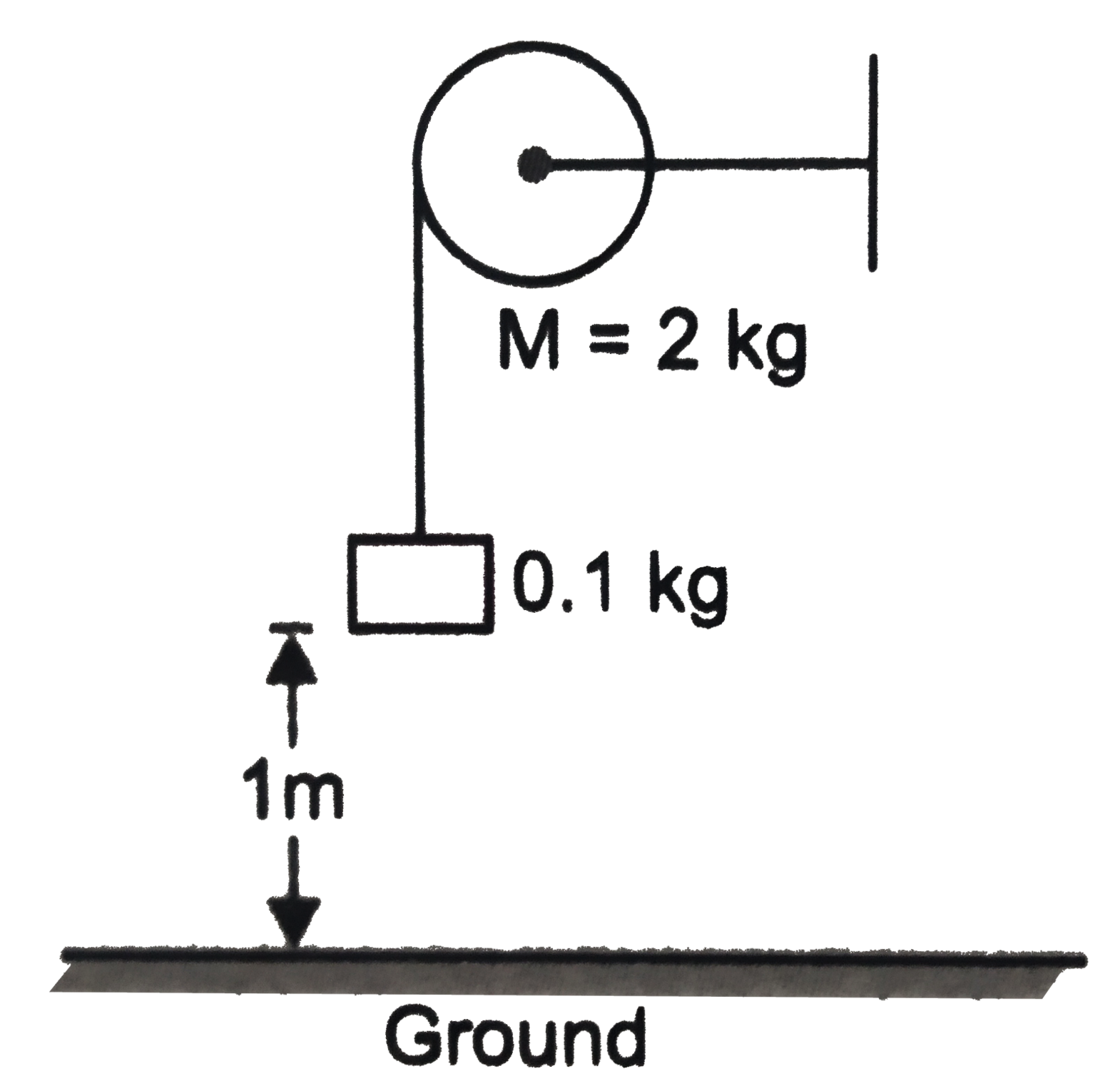 A1120ms−1B2011m/sC1011ms−1D1110ms−1
A1120ms−1B2011m/sC1011ms−1D1110ms−1A 0.075-kg arrow is fired horizontally. The bowstring exerts an average force of 65 N on the arrow over a distance of 0.90 m. With what speed does the arrow leave the bow ?
A39m/sB28m/sC82m/sD66m/sA trolley of mass 20 kg is attached to a block of mass 4kg by massless string passing over a frictionless pulley as shown in the figure. If the coefficient of kinetic friction between trolley and the surface is 0.02, then the acceleration of the trolley and block system is (Takeg=10ms−2)
 A1ms−2B2ms−2C1.5ms−2D2.5ms−2
A1ms−2B2ms−2C1.5ms−2D2.5ms−2
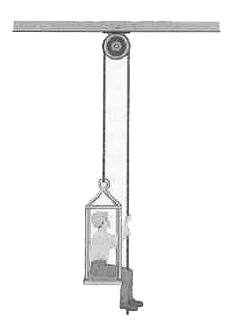
Figure 5-55 shows a man sitting in a bosun's chair that dangles from a mass-less rope, which runs over a massless, frictionless pulley and back down to the man's hand. The combined mass of man and chair is 103.0 kg. With what force magnitude must the man pull on the rope if he is to rise (a) with a constant velocity and (b) with an upward acceleration of 1.30 m/s2 ?
View SolutionA man of mass M stands on the floor of a box of mass m as shown in fig. He raises himself and the box with an acceleration a =g3 by means of a rope going over a fixed frictionless pulley. If the mass of the rope is negligible compared to (M + m) and if M = 2m, the tension in the rope will be?
View SolutionA 10 kg monkey climbs up a massless rope that runs over a frictionless tree limb and back down to a 15 kg package on the ground (Fig. 5-56). (a) What is the magnitude of the least acceleration the monkey must have if it is to lift the package off the ground? If, after the package has been lifted, the monkey stops its climb and holds on to the rope, what are the (b) magnitude and (c) direction of the monkey's acceleratiohn and (d) the tension in the rope ?

View SolutionA cannon of mass 100 kg is kept on a frictionless floor. If a cannon ball of mass 1 kg is fired from it with a speed of 200 m/s. With what velocity the cannon will move ?
View SolutionA cannon of mass 100 kg is kept on a frictionless floor. If a cannon ball of mass 1 kg is fired from it with a speed of 200 m/s. With what velocity the cannon will move?
View Solution
