How can you lower a 100-kg body from the roof of a house using a cord with a breaking strength of 80 kgf (kilogram force) without breaking the rope ?
The correct Answer is:By allowing it to go down with acceleration g/5
To solve the problem of lowering a 100 kg body from the roof of a house using a cord with a breaking strength of 80 kgf without breaking the rope, we can follow these steps:
1. Identify the Forces Acting on the Body:
- The weight of the body (W) acting downwards:
W=Mg=100kg×g
- The tension (T) in the cord acting upwards.
2. Set Up the Equation of Motion:
- When the body is lowered with an acceleration a, the net force acting on the body can be expressed using Newton's second law:
Mg−T=Ma
- Rearranging this gives:
T=Mg−Ma
3. Substitute Values:
- Substitute M=100kg into the equation:
T=100g−100a
4. Determine the Maximum Tension:
- The maximum tension (T_max) that the cord can withstand is given by the breaking strength of the cord:
Tmax=80kgf=80g
5. Set Up the Inequality:
- To ensure the cord does not break, we need:
T≤Tmax
- Substituting the expression for T:
100g−100a≤80g
6. Solve for Acceleration (a):
- Rearranging the inequality gives:
100g−80g≤100a
20g≤100a
a≥20g100=g5
7. Conclusion:
- To lower the 100 kg body safely without breaking the cord, it should be lowered with an acceleration of g5.
- The weight of the body (W) acting downwards:
W=Mg=100kg×g
- The tension (T) in the cord acting upwards.
- When the body is lowered with an acceleration a, the net force acting on the body can be expressed using Newton's second law:
Mg−T=Ma
- Rearranging this gives:
T=Mg−Ma
- Substitute M=100kg into the equation:
T=100g−100a
- The maximum tension (T_max) that the cord can withstand is given by the breaking strength of the cord:
Tmax=80kgf=80g
- To ensure the cord does not break, we need:
T≤Tmax
- Substituting the expression for T:
100g−100a≤80g
- Rearranging the inequality gives:
100g−80g≤100a
20g≤100a
a≥20g100=g5
- To lower the 100 kg body safely without breaking the cord, it should be lowered with an acceleration of g5.
Topper's Solved these Questions
- LAWS OF MOTION, FREE BODY DIAGRAMBOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (B)
34 Videos
- LAWS OF MOTION, FREE BODY DIAGRAMBOOK - NN GHOSHCHAPTER - LAWS OF MOTION, FREE BODY DIAGRAMEXERCISE - Exercise (B)
34 Videos
- KINETIC THEORY OF GASESBOOK - NN GHOSHCHAPTER - KINETIC THEORY OF GASESEXERCISE - All Questions
24 Videos
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBOOK - NN GHOSHCHAPTER - MOMENT, TORQUE, EQUILIBRIUM OF BODIESEXERCISE - Exercises
33 Videos
Similar Questions
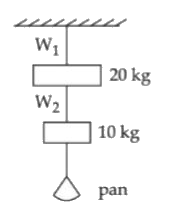
Wires W1 and W2 are made of same material having the breaking stress of 1.25×109N/m2.W1andW2 have cross-sectional area of 8×10−7m2and4×10−7m2, respectively. Masses of 20 kg and 10 kg hang from them as shown in the figure. The maximum mass that can be placed in the pan without breaking the wires is kg. (Use g=10m/s2)
View SolutionA uniform one metre long rod AB of 17 kg weight I suspended horizontally from fixed supports by two vertical strings attached to points C and D on the rod at distances of 12 cm and 16 cm from A and B respectively .The strings at C and D can support weights of 10 kg and 9 kg respectively without breaking .Find where a weight of 2 kg can be attached to the rod without breaking either of the string .
View Solution
Knowledge Check
The acceleration with which an object of mass 100 kg be lowered from a roof using a cord with a breaking strength of 60 kg weight without breaking the rope is- (assume g = 10 m/sec2)
A2m/sec2B4m/sec2C6m/sec2D10m/sec2A uniform one metre long rod AB of weight 17 kg is suspended horizontally from fixed supports by two vertical strings attached to points C and D on the rod at distances of 12 cm and 16 cm from A and B respectively. The strings at C and D can support weights of 10 kg and 9 kg respectively without breaking. Then the position where a weight of 2 kg can be attached to the rod without breaking either of the strings is
A10 cm from AB12 cm from AC13 cm from ADNone of theseA body of mass 60 kg is holding a vertical rope . The rope can break when a mass of 75 kg is suspended from it. The maximum acceleration with which the boy can climb the rope without breaking it is :(g=10m/s2)
A2.5m/s2B5.0m/s2C7.5m/s2D22.5m/s2
A monkey is decending from the branch of a tree with constant acceleration. If the breaking strength is 75% of the weight of the monkey, the minimum acceleration with which monkey can slide down without breaking the branch is
View SolutionA fire man has to carry an injured person of mass 40 kg from the top of a building with the help of the rope which can withstand a load of 100 kg. The acceleration of the fireman if his mass is 80 kg, will be-
View SolutionOne type of steel has density 7800kg/m3 and will break if the tensile stress exceeds 7.0×108N/m2. You want to make a guitar string using 4.0g of this type of steel. While in use, the guitar string must be able to withstand a tension of 900N without breaking.
(a) Determine the maximum length and minimum radius the string can have.
(b) Determine the highest possible fundamental frequency of standing waves on this string, if the entire length of the string is free to vibrate.
View SolutionA stone is accelerated upwards by a cord whose breaking strength is three times the weight of the stone. The maximum acceleration with which the stone can be moved up without breaking the cord is
View SolutionA sphere is accelerated upwards with the help of a cord whose braking strength is five times its weight. The maximum acceleration with which the sphere can move up without cord breaking is :-
View Solution
