How is mutual inductance of a pair of coils affected when (i) separation between the coils in increased, (ii) the number of turns of each coil is increased , (iii) a thin iron sheet is placed between the two coils, other factors ramaining the same ? Explain your answer in each case.
To analyze how the mutual inductance of a pair of coils is affected under different conditions, we will consider the formula for mutual inductance M:
M=μ0N1N2AL
where:
- μ0 is the permeability of free space,
- N1 is the number of turns in the first coil,
- N2 is the number of turns in the second coil,
- A is the cross-sectional area of the coils,
- L is the length of the coils.
Now, let's analyze each case step by step.
(i) When the separation between the coils is increased:
1. Effect on Flux: Increasing the separation between the coils decreases the magnetic flux linkage between them. This is because the magnetic field strength decreases with distance.
2. Impact on Mutual Inductance: Since mutual inductance M is directly proportional to the magnetic flux linked, a decrease in flux leads to a decrease in mutual inductance.
3. Conclusion: Therefore, when the separation between the coils is increased, the mutual inductance decreases.
(ii) When the number of turns of each coil is increased:
1. Effect on Mutual Inductance: The mutual inductance M is directly proportional to the product of the number of turns in each coil, N1 and N2.
2. Impact of Increasing Turns: If the number of turns in each coil is increased, the product N1N2 increases, which directly increases the mutual inductance.
3. Conclusion: Therefore, when the number of turns of each coil is increased, the mutual inductance increases.
(iii) When a thin iron sheet is placed between the two coils:
1. Effect of Iron Sheet: The introduction of an iron sheet increases the permeability of the medium between the coils. The relative permeability μr of iron is much greater than that of air.
2. Impact on Mutual Inductance: The mutual inductance can be expressed as M′=μrM, where M is the original mutual inductance without the iron sheet. Since μr>1, the mutual inductance increases.
3. Conclusion: Therefore, when a thin iron sheet is placed between the two coils, the mutual inductance increases.
Summary of Effects:
- Increased Separation: Decreases mutual inductance.
- Increased Number of Turns: Increases mutual inductance.
- Placement of Iron Sheet: Increases mutual inductance.
- μ0 is the permeability of free space,
- N1 is the number of turns in the first coil,
- N2 is the number of turns in the second coil,
- A is the cross-sectional area of the coils,
- L is the length of the coils.
2. Impact on Mutual Inductance: Since mutual inductance M is directly proportional to the magnetic flux linked, a decrease in flux leads to a decrease in mutual inductance.
3. Conclusion: Therefore, when the separation between the coils is increased, the mutual inductance decreases.
2. Impact of Increasing Turns: If the number of turns in each coil is increased, the product N1N2 increases, which directly increases the mutual inductance.
3. Conclusion: Therefore, when the number of turns of each coil is increased, the mutual inductance increases.
2. Impact on Mutual Inductance: The mutual inductance can be expressed as M′=μrM, where M is the original mutual inductance without the iron sheet. Since μr>1, the mutual inductance increases.
3. Conclusion: Therefore, when a thin iron sheet is placed between the two coils, the mutual inductance increases.
- Increased Separation: Decreases mutual inductance.
- Increased Number of Turns: Increases mutual inductance.
- Placement of Iron Sheet: Increases mutual inductance.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Solved Examples (b)1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Short Answer Qusetions2videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Exercise191videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - II Focus multiple choice question5videos
ELECTROMAGNETIC WAVES
Similar Questions
How does the mutual inductance of a pair of coils change when
(i) distance between the coils is increased and
(ii) number of turns in the coils is increased?View SolutionHow does the mutual inductance of a pair of coils change when
(i) distance between the coils is decreased and
(ii) number of turns in the coils is decreased ?View Solution
Knowledge Check
- Question 1 - Select One
The self inductance of a coil is L . Keeping the length and area same, the number of turns in the coil is increased to four times. The self inductance of the coil will now be
A14LBLC4LD16 L - Question 2 - Select One
If number of turns in primary and secondary coils is increased to two times each, the mutual inductance
Abecomes 4 timesBbecomes 2 timesCbecomes 1/4 timesDremains unchanged - Question 3 - Select One
Coefficient of mutual inductance for two coils is 1 H. Current in one of the coils is increased from 4 to 5 A in 1 ms. What average emf will be induced in the other coil?
A500 VB250 VC750 VD1000 V
The mutual inductance of a pair of coils, each of N turns, is M henry. If a current of I ampere in one of the coils is brought to zero in t second, the emf induced per turn in the other coil, in volt, will be
View SolutionA coil of radius r is placed at the centre of R>>r and coils are in same plane.The coefficient of mutual inductance between the coil is
View SolutionThe mutual inductance between two coils is 0.5H.It the current in one coil is changed at the rate of 5A/s,what will be the emf induced in the other coil?
View SolutionA coil A is connected to a voltmeter V and the other coil B to an alterniting current sourecs, Fig. If a large copper sheet is placed between the two coils, how does the induced emf in coil A change due to current in coil B ?
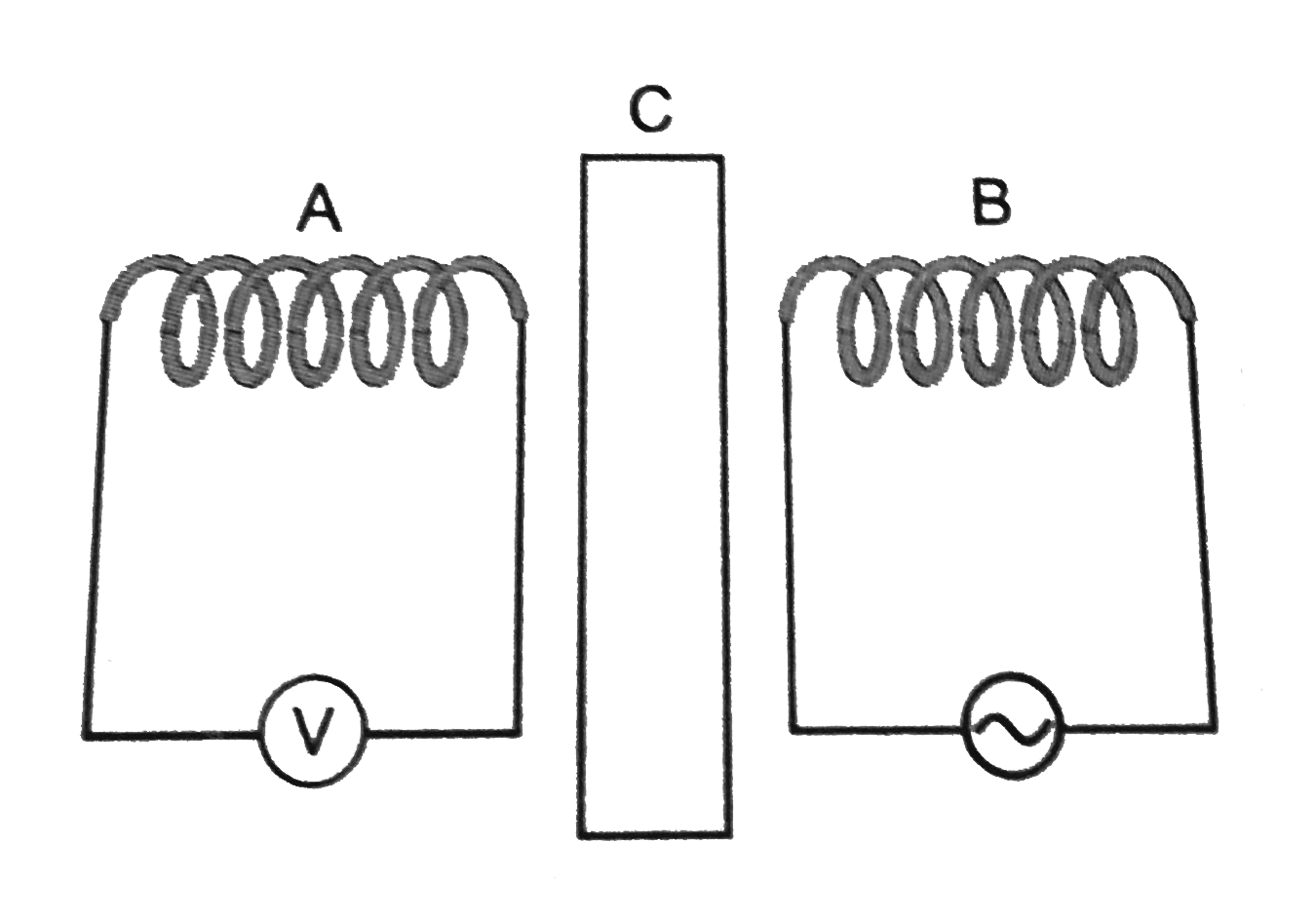 View Solution
View SolutionAn emf 96.0mV is induced in the windings of a coil when the current in a nearby coil is increasing at the rate of 1.20A/s. The mutual inductance of the two coils is
View Solution

