How much should the temperature of a brass rod be increased so as to increase its length by 1%? Given α for brass is 0.00002.∘C−1.
300∘C
400∘C
500∘C
550∘C
The correct Answer is:A
To solve the problem of how much the temperature of a brass rod should be increased to achieve a 1% increase in its length, we can use the formula for linear expansion:
ΔL=αLΔT
Where:
- ΔL = change in length
- L = original length
- α = coefficient of linear expansion
- ΔT = change in temperature
Step 1: Understand the given values
We know:
- The coefficient of linear expansion for brass, α=0.00002∘C−1
- The desired change in length is 1% of the original length, which can be expressed as:
ΔLL=1100
Step 2: Rearrange the formula
From the linear expansion formula, we can express ΔT as:
ΔT=ΔLαL
Step 3: Substitute the values
Since ΔLL=1100, we can express ΔL as:
ΔL=1100L
Now substituting this into the equation for ΔT:
ΔT=1100LαL
Step 4: Simplify the equation
Notice that L cancels out:
ΔT=1100α
Step 5: Substitute α into the equation
Now substituting the value of α:
ΔT=1100×0.00002
Step 6: Calculate ΔT
Calculating the above expression:
ΔT=10.000002=500
Conclusion
Thus, the temperature of the brass rod should be increased by 500∘C.
- ΔL = change in length
- L = original length
- α = coefficient of linear expansion
- ΔT = change in temperature
We know:
- The coefficient of linear expansion for brass, α=0.00002∘C−1
- The desired change in length is 1% of the original length, which can be expressed as:
ΔLL=1100
From the linear expansion formula, we can express ΔT as:
ΔT=ΔLαL
Since ΔLL=1100, we can express ΔL as:
ΔL=1100L
ΔT=1100LαL
Notice that L cancels out:
ΔT=1100α
Now substituting the value of α:
ΔT=1100×0.00002
Calculating the above expression:
ΔT=10.000002=500
Thus, the temperature of the brass rod should be increased by 500∘C.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(AIIMS)28videos
SOLVD PAPERS 2017 NEET, AIIMS & JIPMER
- BOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions14videos
SIMPLE HARMONIC MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - SOUND WAVESEXERCISE - Exercise 19.74videos
SOUND WAVES
Similar Questions
A Carnot engine whose sink is at 300K has an efficiency of 40%. By how much should the temperature of source be increased so as to increase its efficiency by 50% of original efficiency.
View SolutionBy what percentage should the pressure of a given mass of a gas be increased so as to decrease its volume by 10% at a constant temperature?
View Solution
Knowledge Check
- Question 1 - Select One
The moment of inertia of a rod about its perpendicular bisector is I . When the temperature of the rod is increased by ΔT , the increase in the moment of inertia of the rod about the same axis is (Here , α is the coefficient of linear expansion of the rod )
AαIΔTB2αIΔTCαIΔT2D2IΔTα
An ideal engine whose low-temperature reservoir is at 27∘C has an efficiency of 40%. By how much should the temperature of the high-temperature reservoir be increased so as to increase the efficiency to 50% ?
View SolutionThe wire is stretched to increase the length by 1%. Find the percentage change in the resistance.
View SolutionThe diameter of a flywheel is increased by 1% . Increase in its moment of interia about the central axis is
View SolutionA clock which keeps correct time at 25∘C , has a pendulum made of brass. The coefficient of linear expansion for brass is 0.000019.∘C−1 . How many seconds a day will it gain if the ambient temperature falls to 0.∘C ?
View SolutionThe rate of a reaction A doubles on increasing the temperature from 300 to 310 K. By how much, the temperature of reaction B should be increased from 300 K so that rate doubles if activation energy of the reaction B is twice to that of reaction A
View SolutionTwo wires of diameter 0.25cm, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5m and that of brass is 1.0m. Young's modulus of steel is 2.0×1011Pa and that of brass is 1.0×1011 Pa. Compute the ratio of elongations of steel and brass wires. △lsteel△lbrass=?
 View Solution
View SolutionTwo wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in fig. The unloaded length of steel wire is 1.5m and that of brass wire is 1.0m. Compute the elongations of the steel and the brass wires.
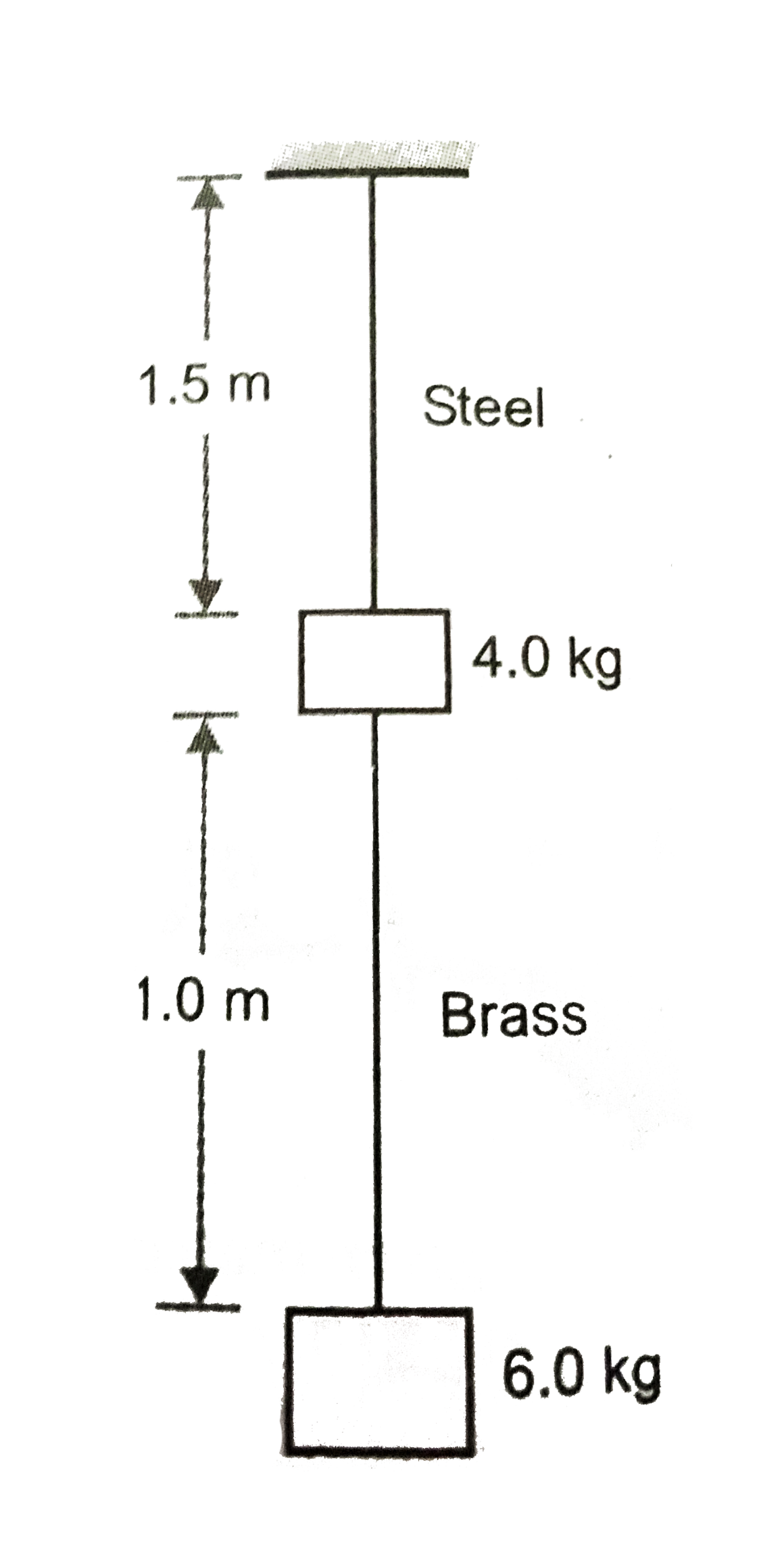 View Solution
View Solution

