How will you prove that the angle of incidence is equal to the angle of reflection?
To prove that the angle of incidence is equal to the angle of reflection, we can conduct a simple experiment. Here’s a step-by-step solution:
1. Gather Materials:
- You will need a white sheet of paper, a mirror, a protractor, and two pins.
2. Prepare the Setup:
- Place the white sheet of paper on a flat surface.
- Draw a straight line on the paper. This line will serve as the baseline for your experiment.
3. Position the Mirror:
- Place the mirror along the straight line you drew. Ensure that it is stable and does not move.
4. Create the Incident Ray:
- Use a pencil to draw an incident ray that strikes the mirror at an angle. This ray represents the light coming towards the mirror.
5. Mark Points on the Incident Ray:
- Place two pins (let's call them Point P and Point Q) on the incident ray, ensuring they are spaced out.
6. Observe the Reflection:
- Look at the reflection of Points P and Q in the mirror. The image of these points will appear behind the mirror.
7. Align the Pins:
- Adjust your view so that you can see Points P and Q, along with their images in the mirror, in a straight line.
8. Mark the Reflected Ray:
- Once you have aligned the pins, place another pin (Point R) along the line of the reflected ray.
9. Draw the Normal Line:
- At the point where the incident ray hits the mirror, draw a normal line (a perpendicular line) to the mirror surface.
10. Measure Angles:
- Using a protractor, measure the angle between the incident ray and the normal line. This is the angle of incidence (i).
- Next, measure the angle between the reflected ray and the normal line. This is the angle of reflection (r).
11. Compare the Angles:
- Check the measurements of angle of incidence (i) and angle of reflection (r). According to the law of reflection, these two angles should be equal.
12. Conclusion:
- If the measurements of the angle of incidence and the angle of reflection are the same, you have successfully proven that the angle of incidence is equal to the angle of reflection.
- You will need a white sheet of paper, a mirror, a protractor, and two pins.
- Place the white sheet of paper on a flat surface.
- Draw a straight line on the paper. This line will serve as the baseline for your experiment.
- Place the mirror along the straight line you drew. Ensure that it is stable and does not move.
- Use a pencil to draw an incident ray that strikes the mirror at an angle. This ray represents the light coming towards the mirror.
- Place two pins (let's call them Point P and Point Q) on the incident ray, ensuring they are spaced out.
- Look at the reflection of Points P and Q in the mirror. The image of these points will appear behind the mirror.
- Adjust your view so that you can see Points P and Q, along with their images in the mirror, in a straight line.
- Once you have aligned the pins, place another pin (Point R) along the line of the reflected ray.
- At the point where the incident ray hits the mirror, draw a normal line (a perpendicular line) to the mirror surface.
- Using a protractor, measure the angle between the incident ray and the normal line. This is the angle of incidence (i).
- Next, measure the angle between the reflected ray and the normal line. This is the angle of reflection (r).
- Check the measurements of angle of incidence (i) and angle of reflection (r). According to the law of reflection, these two angles should be equal.
- If the measurements of the angle of incidence and the angle of reflection are the same, you have successfully proven that the angle of incidence is equal to the angle of reflection.
Topper's Solved these Questions
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - CLASSROOM CORNER (A. Very Short Answer Type Questions) ( Assertion - Reason Type - Questions)
4 Videos
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - CLASSROOM CORNER (B. Short Answer Type Questions )
29 Videos
- LIGHTBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - LIGHTEXERCISE - CLASSROOM CORNER (A. Very Short Answer Type Questions) (Comprehension-Based Questions)
4 Videos
- KINEMATICS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - KINEMATICS EXERCISE - CONCEPT APPLICATION (Level 3) (Application Based Questions )
5 Videos
- MAGNETISM BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - MAGNETISM EXERCISE - CONCEPT APPLICATION (Level 3)
4 Videos
Similar Questions
Light is falling on surface S1, S2, S3 as shown in Fig.16.1.

Surfaces on which the angle of incidence is equal to the angle of reflection is/are
View SolutionLight is falling on the surfaces S1,S2andS3 as shown below:
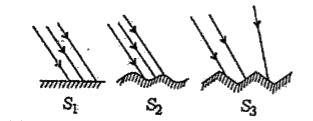
The surfaces on which the angle of incidence is equal to the angle of reflection are
View Solution
Knowledge Check
A ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.ADACBBCDABCBACDDDBACA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.ADACBBCDABCBACDDDBACLight is falling on the surfaces S1,S2andS3 as shown below.

The surfaces on which the angle of incidence is equal to the angle of reflection areAS1andS3BAll the three surfacesCS1andS2DS2andS3
Light is falling on the surfaces S1,S2andS3 as shown below.

The surfaces on which the angle of incidence is equal to the angle of reflection are
View SolutionWhat are the laws of reflection?
(i) The angle of incidence is equal to the angle of reflection, and
(ii) The incident ray, the normal to the mirror at the point of incidence and the reflected ray, all lie in the same plane.
(iii) Incident ray is equal to emergent ray.
(iv) Reflected ray is equal to emergent ray.
View SolutionA light ray incidents at an angle 'i' on a plane mirror and undergoes reflection. Arrange the following steps in sequential order to calculate the angle of deviation of the light ray.
(A) The angle between the incident ray and the extended light ray is 180∘ (B) In case of reflection, the angle of incidence (i) is equal to the angle of reflection (r). Then, the angle between the incident ray and the reflected ray is 2i. (C) Draw an imaginary line, extending the incident light ray, which represents the actual path of the light ray. (D) The angle of deviation is the angle between the reflected light ray and the actual path of the light ray, i.e., 180∘−2i
View SolutionA light ray incidents at an angle 'l' on a plane mirror and undergoes reflection. Arrange the following steps in sequential order to calculate the angle of deviatino of the light ray.
The angle between the incident ray and the extended light ray is 180∘.
In case of reflection, the angle of incidence (i) is equal to the angle of reflection (r). Then the angle between the incident ray and the reflected ray is 2i.
Draw an imaginary line, extending the incident light ray, which reprsesnts the actual path of the light ray.
The angle of deviation is the angle between the reflected light ray and the actual path of the light ray, i.e., 180∘−2i.
View SolutionThe angle of incidence is equal to angle of reflection is the statement of law of
View Solution
