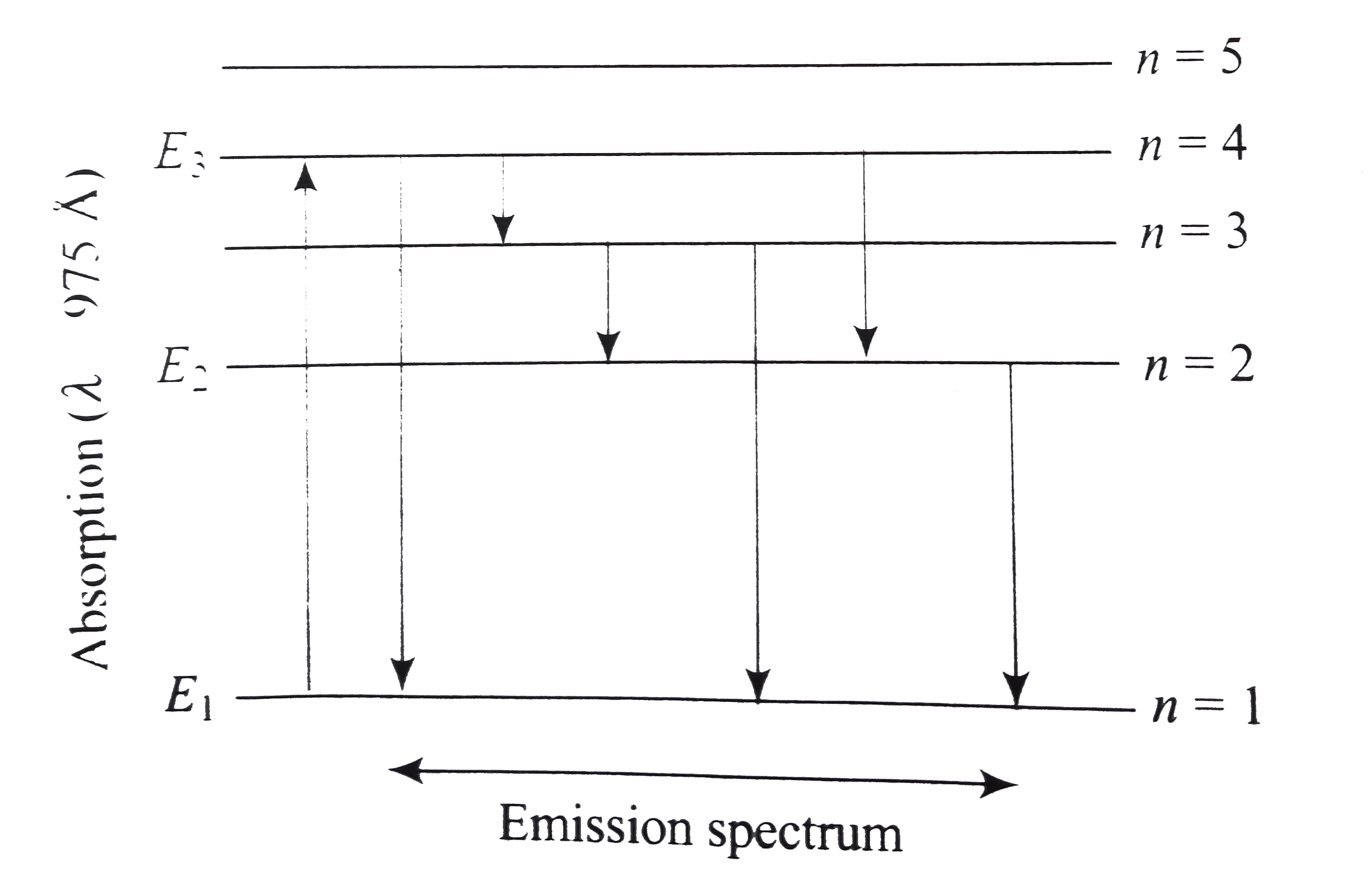
Hydrogen atom is ground state is excited by mean of monochromatic radiation of wavelength 975Å How many different lines are possible in the resulting spectrum ? Calculate the longest wavelength for hydrogen atom as ionization energy is13.6eV

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The energy of an electron in nth orbit of hydrogen (Z=1) is given by En=−Rhcn2
∴Lonizatione≠rgy=E∞−E1=Rhc=13.6eV
∴En13.6n2eV
Therefore, energy of electron in ground state (n=1),
E1=−13.61=−13.6eV
energy of electron in the first excited state (n=2).
E2=−13.622=−13.64=−3.4eV
The energy of electron in the second excited state (n=3).
E3=−13.633=13.69=−1.511eV
ocr_image
The energy of electron in the third excited state (n=4).
E4=−13.642=−13.616=−0.85eV
Energy of incident photon of wavelength
λ=975Å=975×10−10m
E=hcλ=6.63×10−34×3×108975×10−10J
=6.63×10−34×3×108975×10−10×1.6×10−19eV=12.75eV
When incident photon of this energy is absorbed by hydrogen atom, let its ground state electron accupy (n−1)th excited state or nth orbit. Then,
E=−Rhcn2−(−Rhc12)=Rhc(1−1n2)
i.e. , 12.75eV=13.6eV(1−1n2)
This gives n=4 .
That is the electron is excited to the third excited state . The emission spectrum will contain the transition (4→3) for which the energy different is minimum.
i.e. Emin=E4−E3=−0.85−(−1.511)eV
=1.511−0.85=0.661eV
=0.661×1.6×10−19J
∴λmin=hcEmin=6.63×10−34×3×108975×0.661×1.6×10−19=18.807×10−7m
=18807Å

Updated on:21/07/2023
|
Class 12PHYSICSATOMS

Topper's Solved these Questions

Similar Questions