(i) A very long wire carrying a current I is bent at right angles .Find magnetic field at a point lying on a perpendicular to the wire , drawn through the point of bending at a distance d from it
(ii) Three long wires carrying same currect are placed as shown Find magnetic field at O.
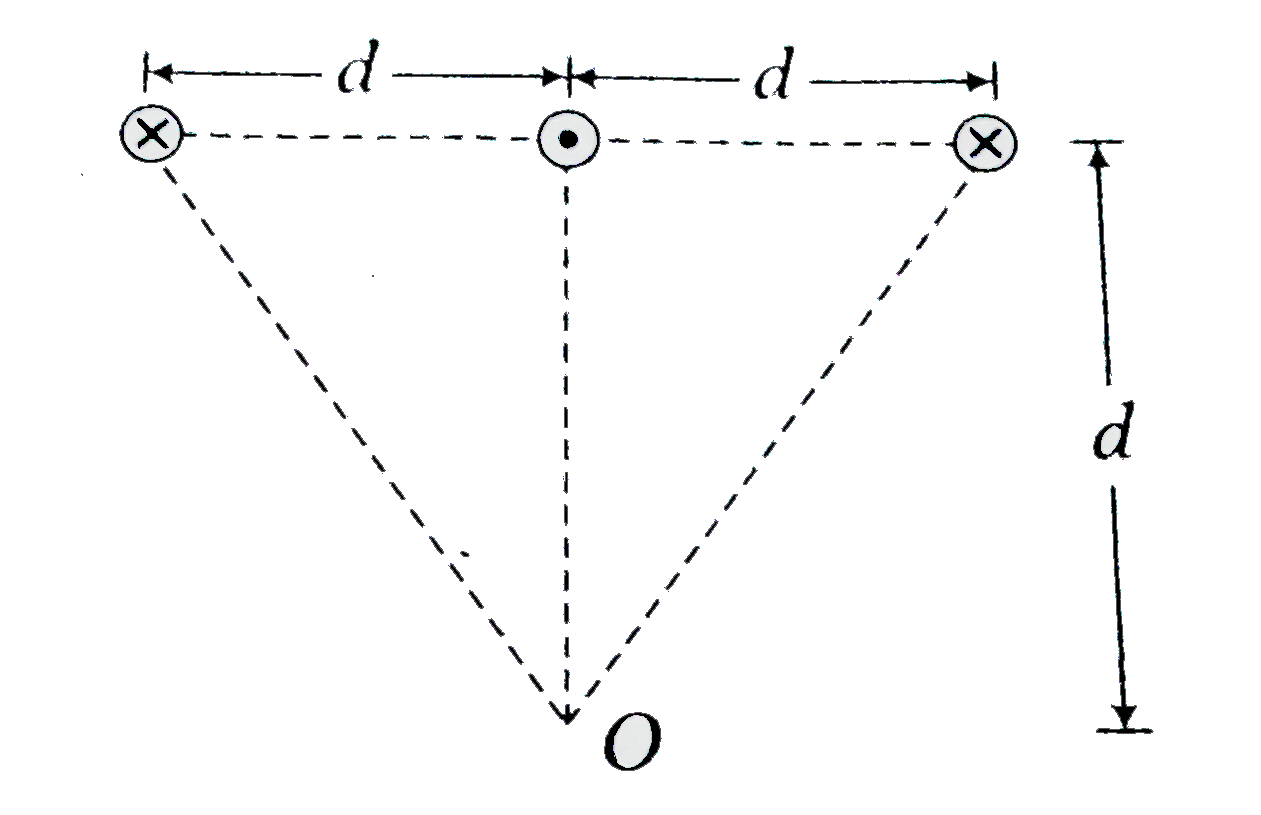
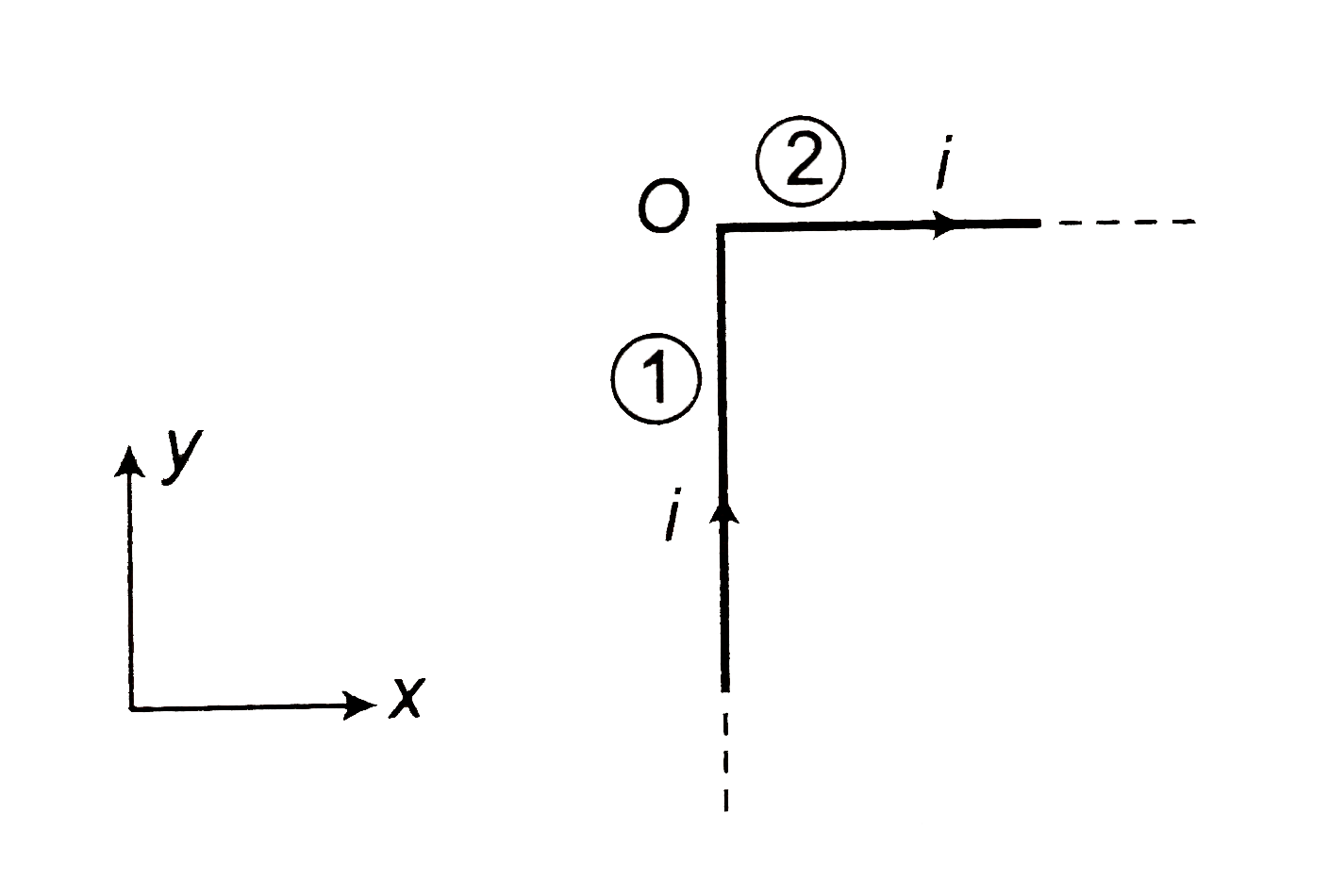
Magnetic field at point P at height d above point O
Due to wire ①, B1=μ0i4πd, towards +x-axis
Due to wire ②, B2=μ0i4πd, towards −y-axis
B1is⊥ar to B2

BP=√2B=√2μ0i4πd
=μ0i2√2πd
(b) 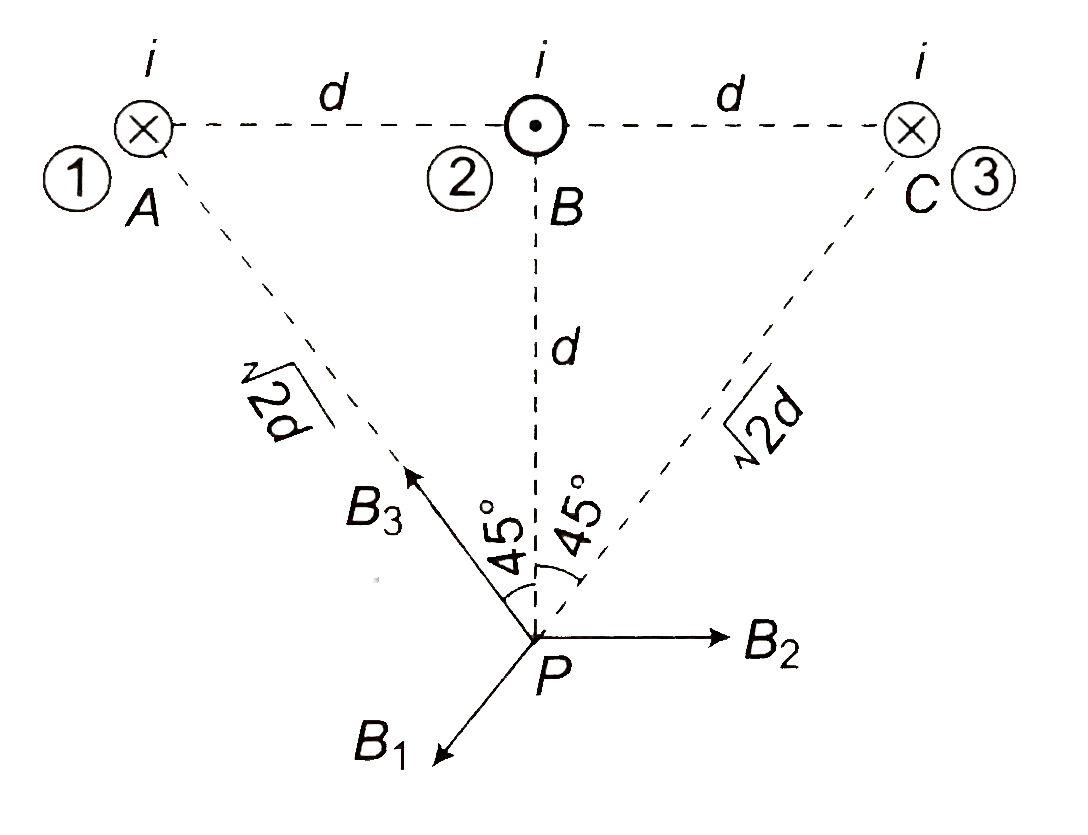
At P:
Due to wire ①, B1=μ0i2π√2d
Due to wire ②, B2=μ0i2πd
Due to wire ③, B3=μ0i2π√2d=B1
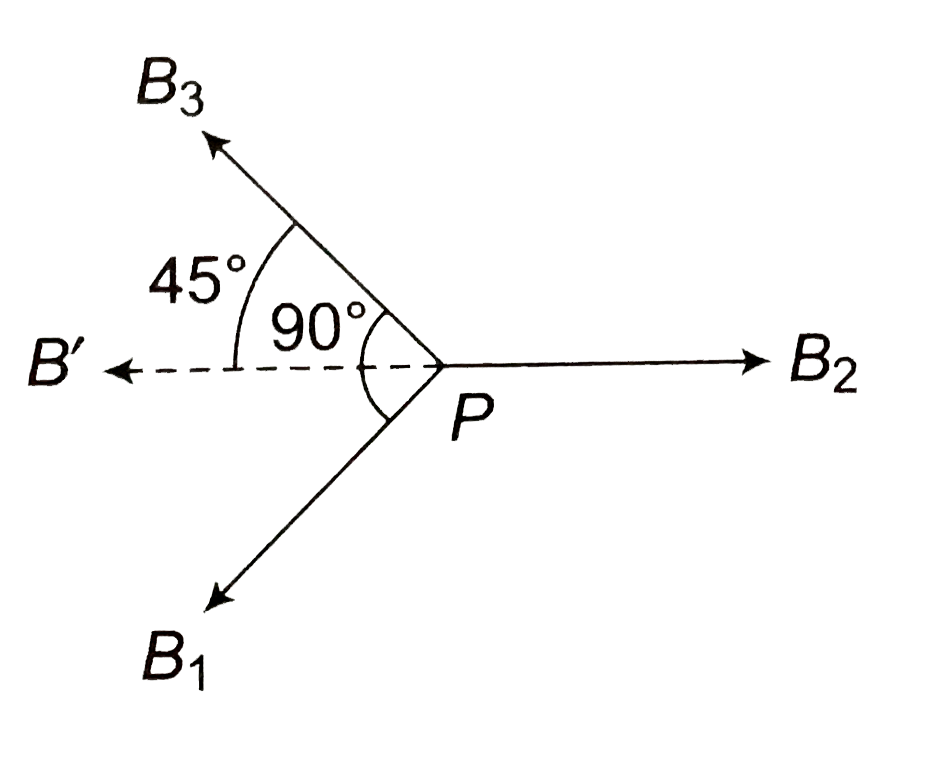
Resultant of B1 and B3 is
B'=2B1cos45∘
=μ0i2πd

B'=B2
BP=0
(c) 
At point B:
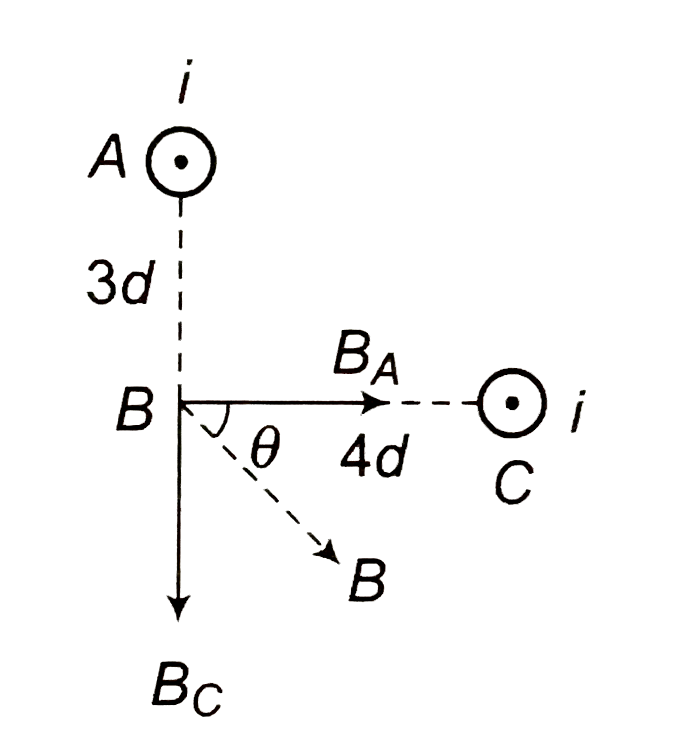
At B:
Due to wire A,BA=μ0i2π(3d), along BC
Due to wire C,BC=μ0i2π(4d), along AB
Resultant magnetic field at B,
B=√B2A+B2C=μ0i2πd√132+142
=μ0i2πd.53×4=524μ0iπd
tanθ=BCBA=34⇒θ=tan−1(3/4)
At point C:
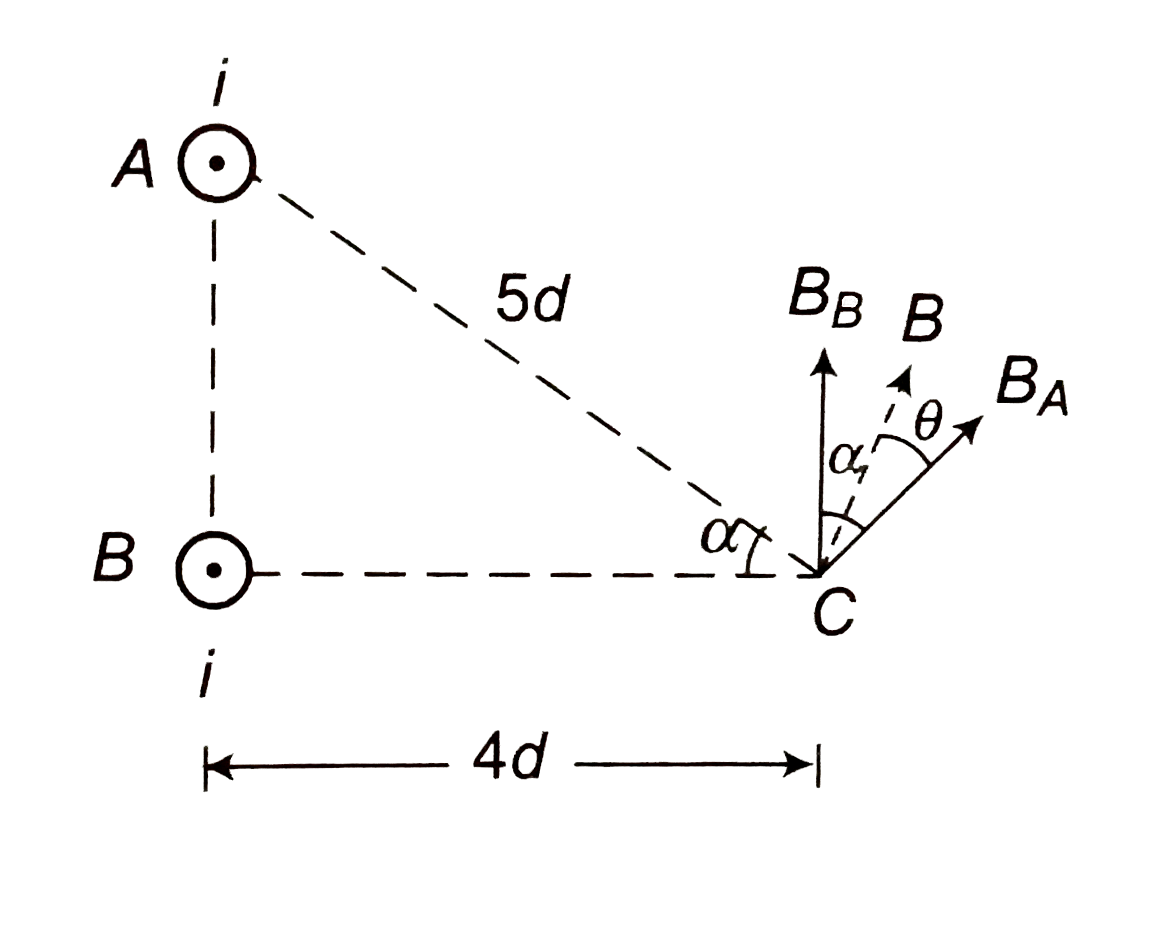
At C:
Due to wire, A,BA=μ0i4π(5d)
Due to wire, A,BB=μ0i2π(4d)
Resulatant magnetic field at C
B=√B2A+B2B+2.BA.BBcosα
=μ0i2πd√152+142+2×15×14×45
=√73μ0i40πd
tanθ=BBsinαBA+BBcosα=14×3515+14×45=38
θ=tan−1(3/8)
Topper's Solved these Questions
Similar Questions
A very long wire carrying a current I=5.0A A is bent at right angles. Find the magnetic induction at a point lying on a perpendicular to the wire, drawn through the point of hending at a distance l=35cm from it.
View SolutionA very long wire carrying a current I=5.0A A is bent at right angles. Find the magnetic induction at a point lying on a perpendicular to the wire, drawn through the point of hending at a distance l=35cm from it.
View Solution
Knowledge Check
A long wire carrying a current i=2A is bent at right angles . The magnetic field lying on a perpendicular normal to the plane of the wire draw through the point of bending at distance 1 m form it is ………….Tesla.
A2×10−7B4√2×10−7C√2×10−7D2√2×10−7A long wire carrying a current i is bent to form a plane angle. The magnitude of magnetic field at height d, above the point of bending
A√2μ0i4πdB3√2μ0i4πdC5√2μ0i4πdD7√2μ0i4πdA long wire carrying i is bent to form a plane angle θ.Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex is written in the form of Kcotθ4Tesla.Then, find the value of K.
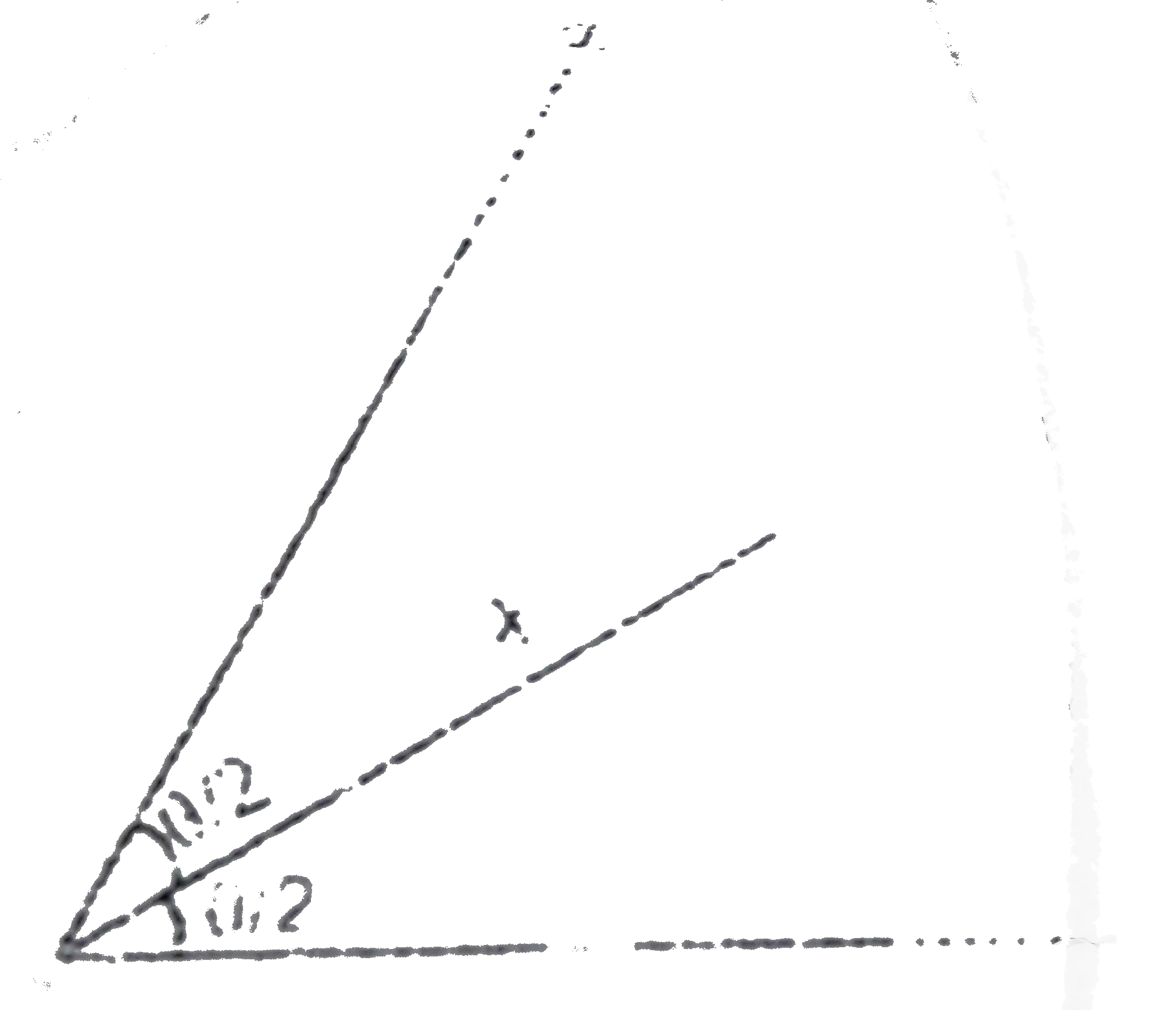 Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
Aμ0iπdcot(θ4),⊙Bμ0i2πdcot(θ4),⊙Cμ0i4πdcot(θ2),⊙Dμ0i4πdcot(θ4),⊙
A very long wire carrying a current I=5.0A is bent at right angles. Find the magnetic induction at a point lying on a perpendicular normal to the plane of the wire drawn through the Point of bending at a distance l=35cm from it.
View SolutionAlongwirecarry∈gacurrentiisbent→formapla≠∠α. F∈dthemag≠ticfieldBatap∮onthebisec→rofthis∠situatedatadistancexomthevertex.
View SolutionFind magnitude and direction of magnetic field at point P in the following cases.
(a)
(b)
P is the centre of square.
(c)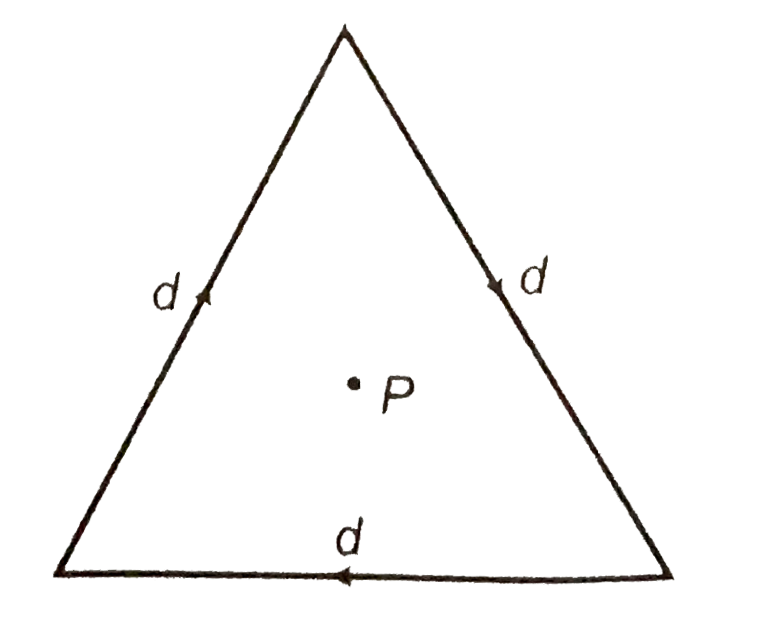
P is the centre of equilateral triangle.
(d)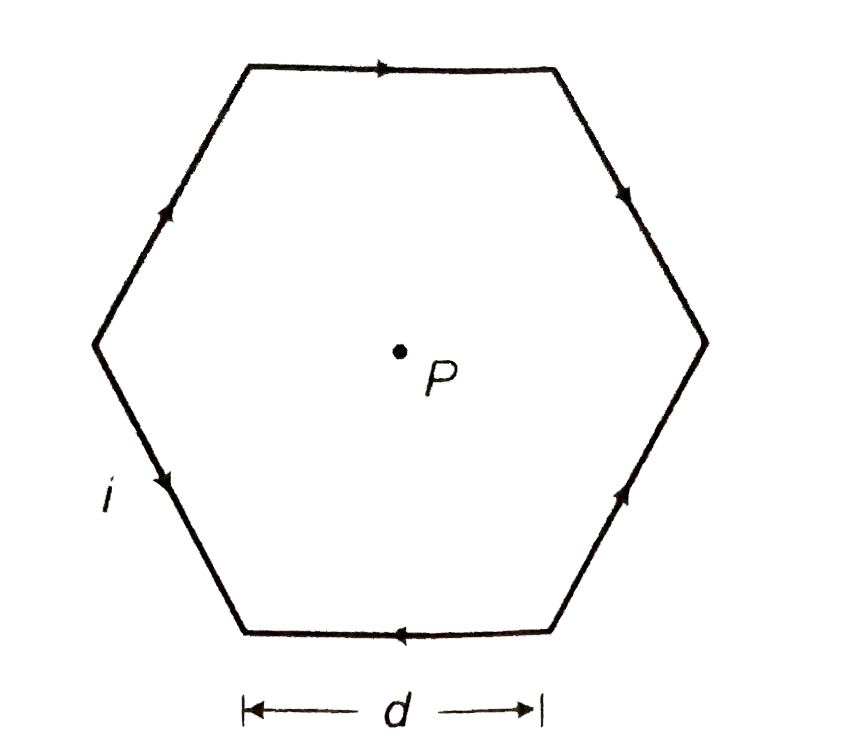
P is the centre of regular hexagon.
(e)
P is the centre of rectangular loop.
(f)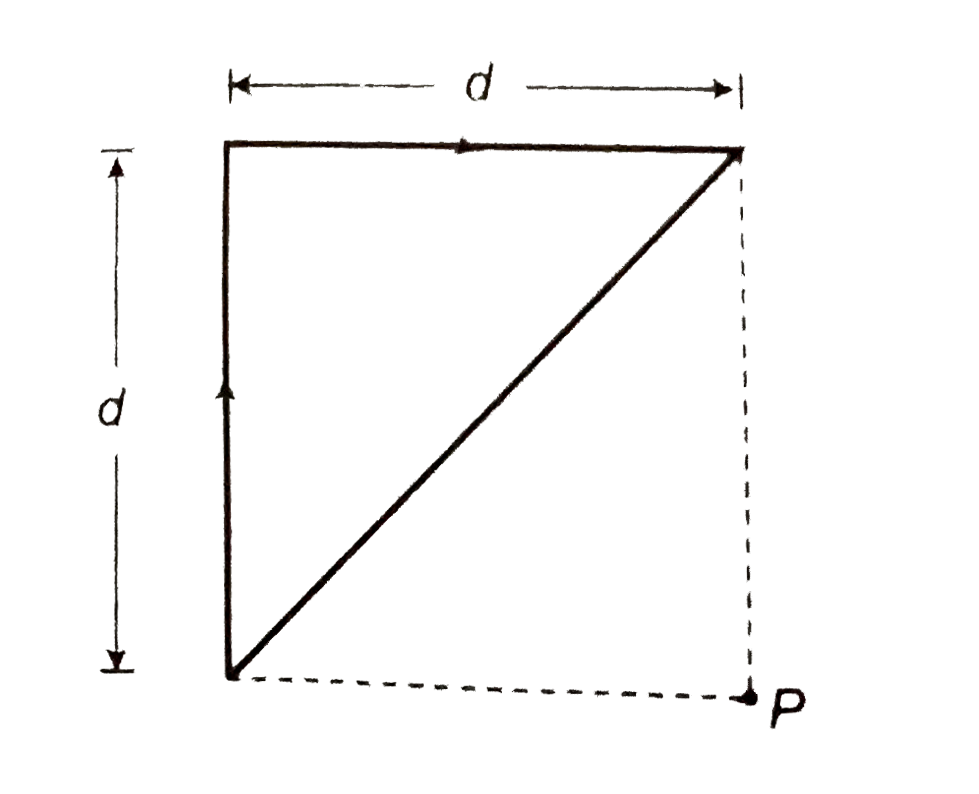
(g) A long wire carrying a current i is bent to from a plane angle θ. Find magnetic field at a point on the bisector of this angle is situated at a distance d from vertex.

(h) A long, straight wire carriers a current i. Let B1 be the magnetic field at a point P at a distance d from the wire. consider a section of length l of this wire such that the point P lies on a perpendicular bisector of the sector. Let B2 be the magnetic field at this point due to this section only. find the value of d/l so that B2 differes from B1 by 1%.
View SolutionThe magnetic field at a distance r from a long wire carryimg current I is 0.4 T. The magnetic field at a distance 2r is
View SolutionA long conducting wire carrying a current I is bent at 120∘( see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is
(μ0 is the permeability of free space)

View Solution
