(i) Three balls 1, 2 and 3 lie on a smooth horizontal table. Ball 1 is given a velocity towards ball 2. Kinetic energy given to ball 1 is . It collides with 2 and in turn ball 2 hits ball 3. All collisions are head on elastic. Masses of the balls are m, M and m respectively.
![(i) Three balls 1, 2 and 3 lie on a smooth horizontal table. Ball 1 is given a velocity towards ball 2. Kinetic energy given to ball 1 is k(0). It collides with 2 and in turn ball 2 hits ball 3. All collisions are head on elastic. Masses of the balls are m, M and m respectively. (a) Calculate the kinetic energy (k3) of ball 3 after ball 2 hits it. (b) Draw the variation of k(3) as a function of M. (ii) Consider 10 balls laid on a smooth surface with masses m,(m)/(2),(m)/(4),(m)/(8)......(m)/(512) and first ball is pushed towards the second with kinetic energy k(0). [All collisions are elastic and head on]. The kinetic energy acquired by the last ball is k(10). In a separate experiment the 10^(th) ball is pushed towards 9^(th) ball with kinetic energy k(0). This time the kinetic energy acquired by 1^(st) ball is k(1). Compare k(10) and k(1)](https://d10lpgp6xz60nq.cloudfront.net/physics_images/IJA_PHY_V01_C05_E01_067_Q01.png)
(a) Calculate the kinetic energy of ball 3 after ball 2 hits it.
(b) Draw the variation of as a function of M.
(ii) Consider 10 balls laid on a smooth surface with masses and first ball is pushed towards the second with kinetic energy . [All collisions are elastic and head on]. The kinetic energy acquired by the last ball is . In a separate experiment the ball is pushed towards ball with kinetic energy . This time the kinetic energy acquired by ball is .
Compare

The correct Answer is:(i) (a)
(b)
(ii)
Step by step video, text & image solution for (i) Three balls 1, 2 and 3 lie on a smooth horizontal table. Ball 1 is given a velocity towards ball 2. Kinetic energy given to ball 1 is k_(0). It collides with 2 and in turn ball 2 hits ball 3. All collisions are head on elastic. Masses of the balls are m, M and m respectively. (a) Calculate the kinetic energy (k_3) of ball 3 after ball 2 hits it. (b) Draw the variation of k_(3) as a function of M. (ii) Consider 10 balls laid on a smooth surface with masses m,(m)/(2),(m)/(4),(m)/(8)......(m)/(512) and first ball is pushed towards the second with kinetic energy k_(0). [All collisions are elastic and head on]. The kinetic energy acquired by the last ball is k_(10). In a separate experiment the 10^(th) ball is pushed towards 9^(th) ball with kinetic energy k_(0). This time the kinetic energy acquired by 1^(st) ball is k_(1). Compare k_(10) and k_(1) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Three balls A, B and C are placed on a smooth horizontal surface. Given that mA=mC=4mB. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collisions between the balls. All collisions are elastic.
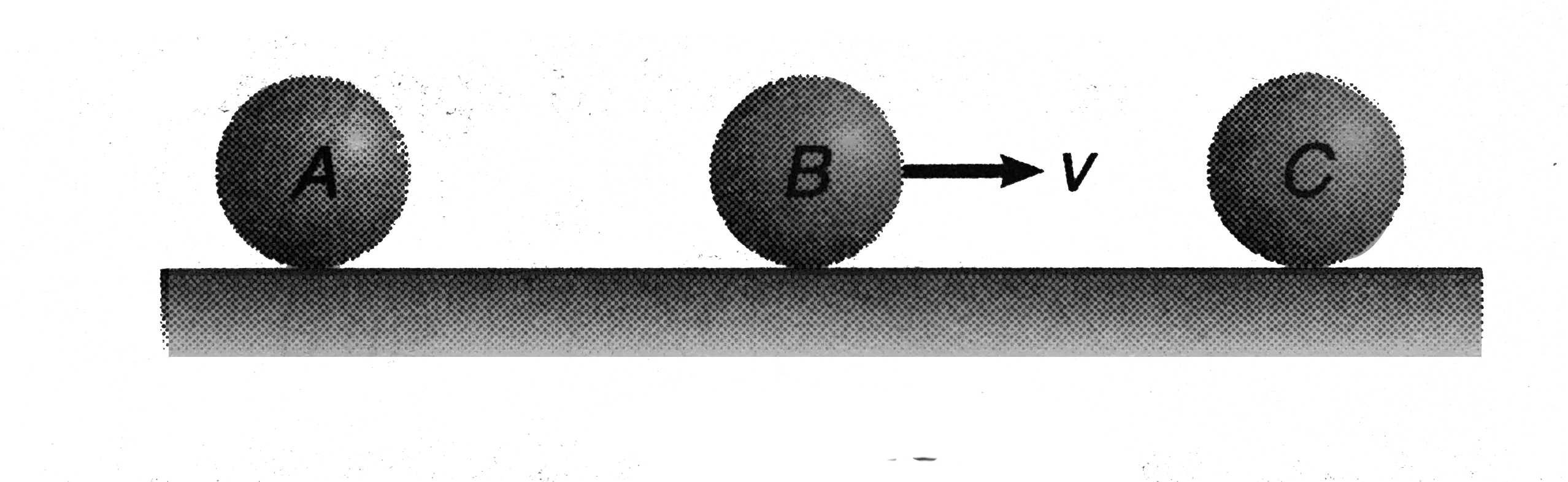
View SolutionThree balls A,B and C(mA=mC=4mB) are placed onn a smooth horizontal surface. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collision betwenent the balls (all collisions are elastic).
View Solution
Knowledge Check
Two balls A & B of mass m1 and m2 are kept on a horizontal smooth surface. A is given a velocity towards B so that they perform head on collision
AIf m1=m2 and collision is elastic. A stops and B moves with the velocity of A after collisionBImpulses on A and B during collision are same in magnitude whether it is elastic or inelastic collisionCImpulses on A and B collision are equal in magnitude only if m1=m2DIf m1>m2, though impulses are same in magnitude velocity of A is still the same direction.A cricket ball is hit for a six the bat at an angle of 45∘ to the horizontal with kinetic energy K. At the highest point, the kinetic energy of the ball is
AzeroBKCK/2DK/√2Consider the situation as shown in the diagram , the ball strikes the wall normally and the collision is elastic , the change in the kinetic energy of the ball is
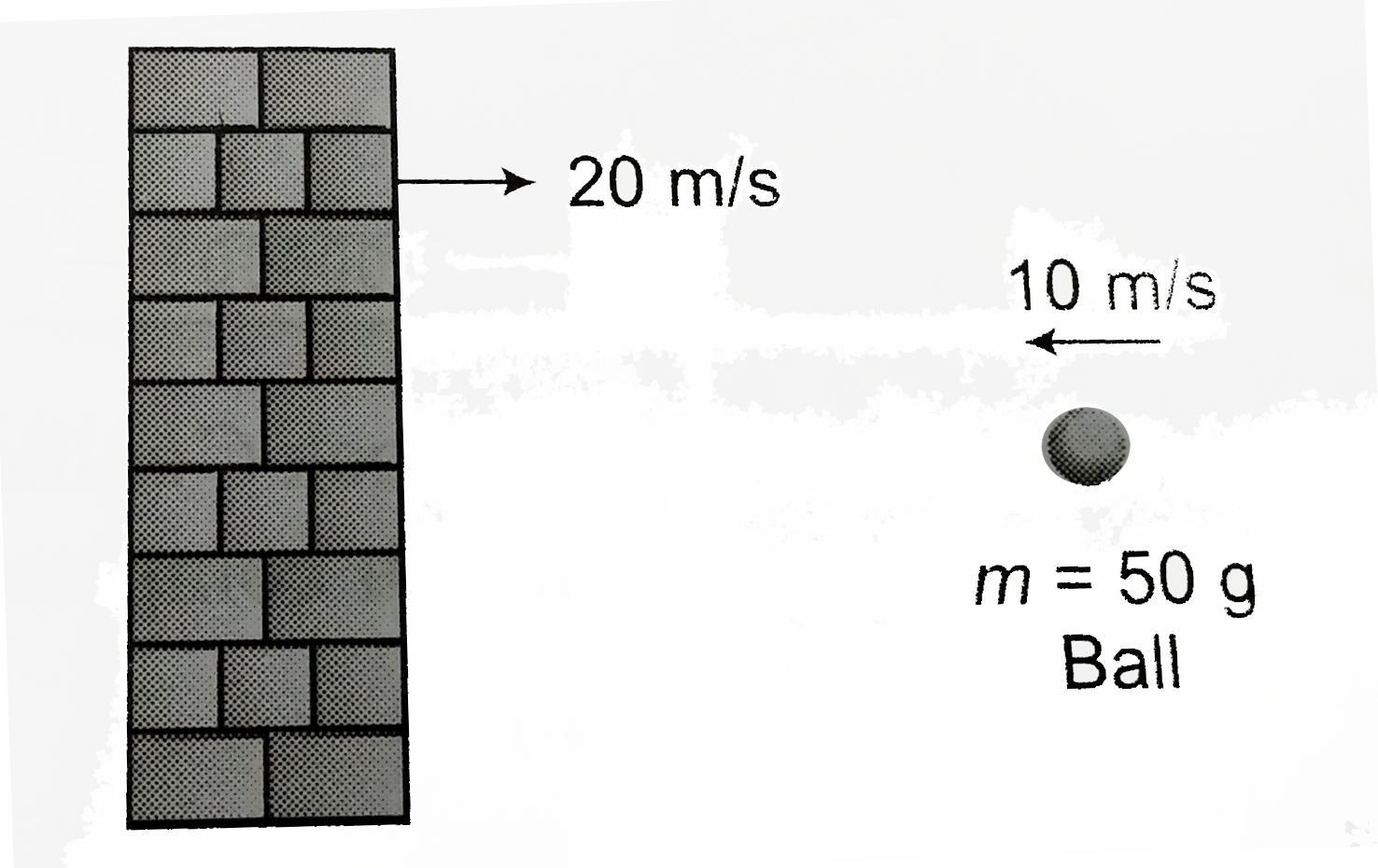 A30JB60JC90JD120J
A30JB60JC90JD120J
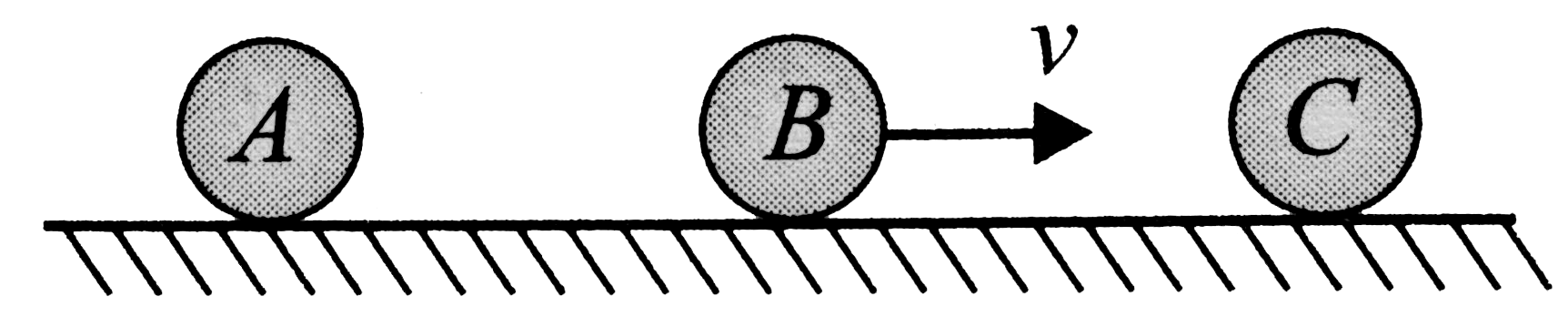
Three balls A,B and C of same mass m are placed on a frictionless horizontal plane in a straight line as shown. Ball A is moved with velocity u towards the middle ball B. If all the collisions are elastic, find the final velocities of all the balls.

View SolutionThree identical balls 1, 2 and 3 are placed together at rest on a smooth horizontal surface. A fourth identical ball moving with velocity u in line of first three balls collides head on elastically as shown in figure, then
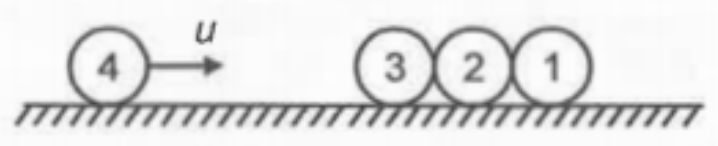
View SolutionA ball of mass m1, collides elastically and head on with ball of mass m2 at rest. Then
View SolutionA steel ball of mass m is moving with a kinetic energy K. The de-Broglie wavelength associated with the ball is
View SolutionA spherical ball of mass m1 colliddes head on with another ball of mass m2 at rest . The collision is elastic . The fraction of kintic energy lost by m1 is :
View Solution
