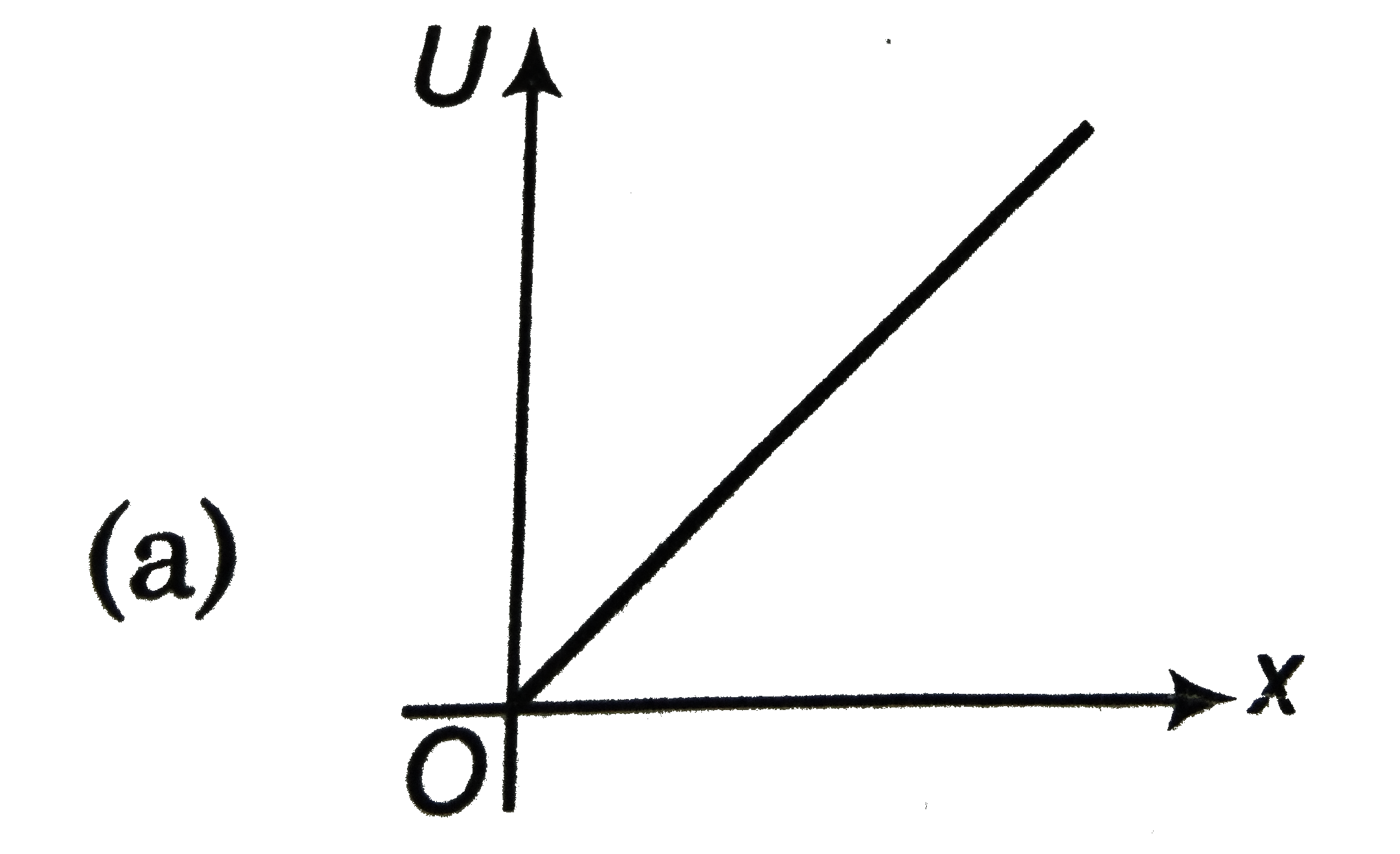
Identify the correct variation of potential energy U as a function of displacement x from mean position (or x2) of a harmonic oscillator (U at mean position =0)


None of these
The correct Answer is:C
U=12kx2
i.e. U versus x2 graph is a straight line passing through origin.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Subjective
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2 Single Correct
28 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
In a simple harmonic oscillator, at the mean position
View SolutionAcceleration of a particle in SHM at displacement x=10cm (from the mean position is a=−2.5cm/s2). Find time period of oscillations.
View SolutionFor examples , find the potential energy of the block at 0.05 m from the mean position
View SolutionFor a particle executing SHM, x = displacement from mean position, v = velocity and a = acceleration at any instant, then
View SolutionWhich of the following quantities is always negative is SHM ?
Here, x is displacement , from mean position.
View SolutionA 20g particle is oscillating simple harmonically with a period of 2sec and maximum kinetic energy 2J. The total mechanical energy of the particle is zero , find
a Amplitude of oscillation
b. potential energy as a function of displacement x relative to mean position.
View SolutionThe variation of potential energy U of a body moving along x - axis varies with its position (x) as shown in figure
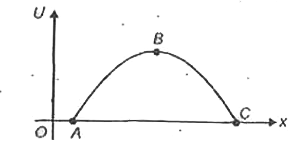
The body is in equilibrium state at
View SolutionThe variations of potential energy (U) with position x for three simple harmonic oscillators A, B and C are shown in figure. The oscillators have same mass. The time period of oscillation is greatest for

View Solutionfind the potential energy of the block at 0.05 m from the mean position
View SolutionAt x=A4, what fraction of the mechanical energy is potential ? What fraction is kinetic ? Assume potential energy to be zero at mean position.
View Solution
