For examples , find the potential energy of the block at 0.05 m from the mean position
To find the potential energy of a block at a distance of 0.05 m from the mean position in a spring-mass system, we can follow these steps:
1. Identify the System:
We have a spring-mass system where a block of mass m is attached to a spring with spring constant k. The block is displaced from the mean position by x=0.05m.
2. Understand the Potential Energy Formula:
The potential energy U stored in a spring when it is displaced by a distance x from its equilibrium position is given by the formula:
U=12kx2
3. Substitute the Values:
We need to substitute x=0.05m into the potential energy formula. However, we need the value of the spring constant k to calculate the potential energy. For the sake of this calculation, let’s assume k is known or given.
4. Calculate the Potential Energy:
U=12k(0.05)2
U=12k⋅0.0025
U=12k⋅2.5×10−3
5. Final Expression:
The potential energy of the block at a distance of 0.05 m from the mean position is:
U=1.25×10−3kJ
Here, k is the spring constant in N/m.
We have a spring-mass system where a block of mass m is attached to a spring with spring constant k. The block is displaced from the mean position by x=0.05m.
The potential energy U stored in a spring when it is displaced by a distance x from its equilibrium position is given by the formula:
U=12kx2
We need to substitute x=0.05m into the potential energy formula. However, we need the value of the spring constant k to calculate the potential energy. For the sake of this calculation, let’s assume k is known or given.
U=12k(0.05)2
U=12k⋅0.0025
U=12k⋅2.5×10−3
The potential energy of the block at a distance of 0.05 m from the mean position is:
U=1.25×10−3kJ
Here, k is the spring constant in N/m.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)58videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )25videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Assignment (Section D) (ASSERTION-REASON TYPE QUESTIONS)13videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)4videos
PHYSICAL WORLD
Similar Questions
If force constant = 100 N/m, find the potential energy of the block at 0.05 m from the mean position
Hint :P.E.=12kx2View SolutionA block whose mass is 2 kg is fastened on a spring whose spring constant is 100 Nm−1 . It is pulled to a distance of 0.1 m from over a frictionless surface and is released at t=0. Calculate the kinetic eneryg of the block when it is 0.05 m away from its mean position.
View Solution
Knowledge Check
- Question 1 - Select One
A block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 100N/m. the block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. the kinetic energy and potential energy of the block when it is 5 cm away from the mean position is
A0.0375 J, 0.125 JB0.125 J, 0.375 JC0.125 J, 0.125 JD0.375 J, 0.375 J
A block whose mass is 1 kg is fastened to a spring.The spring has a spring constant 50Nm−1. The block is pulled to a distance x=10cm from its equilibrium position at x=0 on a frictionless surface at t=0. Calculate the kinetic, potential and total energies of the block when it is 5cm away from the mean position.
View SolutionForce acting on a particle is F=−8x in S.H.M. The amplitude of oscillation is 2 (in m) and mass of the particle is 0.5 kg. The total mechanical energy of the particle is 20 J. Find the potential energy of the particle in mean position (in J).
View SolutionDefine potential energy with an example.
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
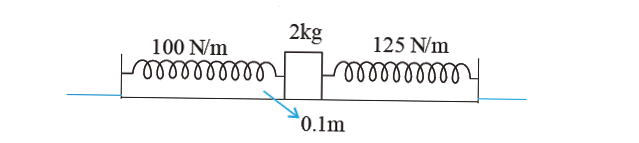
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.View SolutionA block A, weighing 100 N is pulled up a slope of length 5 m by means of a constant force F (= 100 N) as illustrated in Fig.

(a) What is the work done by the force F in moving the block A 5 m along the slope ?
(b) What is the increase in potential energy of the block A?
(c) Account for the difference in the work done by the force and the increase in potential energy of the blockView SolutionFor any S.H.M., amplitude is 6 cm . If instantaneous potential energy is half the total energy then distance of particle from its mean position is
View SolutionThe total energy of a harmonic oscillator of mass 2 kg is 9 J. If its potential energy at mean position is 5 J , its KE at the mean position will be
View Solution

