If a ball strikes with a velocity u1 at the wall which itself is approaching it with a velocity u2 then find the velocity of the ball after collision with the wall.
As the wall is heavy so after collison it will continue to move with the same velocity u2. Relative velocity of separation is equal to relative velocity of approach. Hence,
v1−v2=e(u1−u2)
⇒v1(−u2)=−e[u1−(−u2)]
⇒v1=−e(u1+u2)−u2
In case of perfectly elastic collision e=1
v1=−u1−u2−u3=−(u1+2u2)
Negative sign indicates backward direction.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples13videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
If a ball strikes with a velocity u1 at the wall which itself is approaching it with a velocity u2 then find the velocity of the ball after collision with the wall.
View SolutionA ball of mass m moving with a speed u1 collides elasticity with another identical ball moving with velocity u2.
(a) Find the velocities of the balls after collision if the impact is direct.
(b) Find the angle between velocities after collision if they collide obliquely and u2=0View Solution
Knowledge Check
- Question 1 - Select One
A ball falls from a height of 5 m and strikes a lift which is moving in the upward direction with a velocity of 1ms−1, then the velocity with which the ball rebounds after collision will be
A11ms−1 downwardsB12ms−1 upwardsC13ms−1 upwardsD12ms−1 downwards - Question 2 - Select One
If a ball is thrown up with a velocity v from the top of a building the ball reaches the ground with a velocity 3u. Find the height of the building.
A9u2/gB6u2/gC4u2/gD3u2/g - Question 3 - Select One
A wall moving with velocity 2cms−1 towards the ball and ball is moving towards the wall with a velocity 10cms−1. It hits the wall normally and makes elastic collision with wall. The velocity of ball after collision with wall in cms−1.
A12B8C14D16
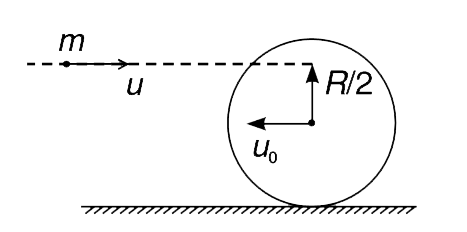
A heavy ball of radius R is travelling on a smooth horizontal surface with a velocity of u0 towards left. A horizontally moving small ball of mass m strikes it at a height R2 above the centre while travelling with velocity u towards right.
(a) After collision the small ball moves in vertically upwards direction with velocity u. Prove that this can happen only if u>√3u0
(b) Find the velocity of small ball after collision if the collision is elastic and the balls are smooth.View SolutionA ball moving with a velocity v strikes a wall moving toward the wall with a velocity u. An elastic impact occurs. Determine the velocity of the ball after the impact. What is the cause of the change in the kinetic energy of the ball ? Consider the mass of the wall to be infinitely great.
 View Solution
View SolutionA particle of mass m moves with velocity u1=20m/s towards a wall that is moving with velocity u2=5m/s. If the particle collides with the wall without losing its energy, find the speed of particle just after the collision.
 View Solution
View SolutionA small ball of mass m collides with as rough wall having coefficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves with angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.
 View Solution
View SolutionA ping-pong ball strikes a wall with a velocity of 10ms−1. If the collision is perfectly elastic, find the velocity if ball after impact
View Solution

