If a body is to be projected vertically upwards from earth's surface to reach a height of 10R where R is the radius of earth. The velocity required to be si is
√2411gr
√2211gr
√2011gr
√1811gr
The correct Answer is:C
From law of conservation of energy, we have
−GMmR+12mυ2=−GMm(10R+R)+0=−GMm11R
or 12υ2=GMR−GM11R=1011GMR
or υ2=2011GMR=2011gR or υ=√20gR11
Similar Questions
The initial velocity vi required to project a body vertically upward from the surface of the earth to reach a height of 10R, where R is the radius of the earth, may be described in terms of escape velocity ve such that vi=√xy×ve. The value of x will be __________ .
View SolutionCalculate the velocity with which a body must be thrown vertically upward from the surface of the earth so that it may reach a height of 10R, where R is the radius of the earth and is equal to 6.4×106m. (Given: Mass of the earth =6×1024kg, gravitational constant G=6.7×10−11Nm2kg−2)
View Solution
Knowledge Check
A body is to be projected vertically upwards from earth's surface to reach a height of 9R, where R is the radius of earth. What is the velocity required to do so? Given g=10ms−2 and radius of earth=6.4×106m.
A1.073×104ms−1B1.73×104ms−1C10.73×104ms−1D17.3×104ms−1A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A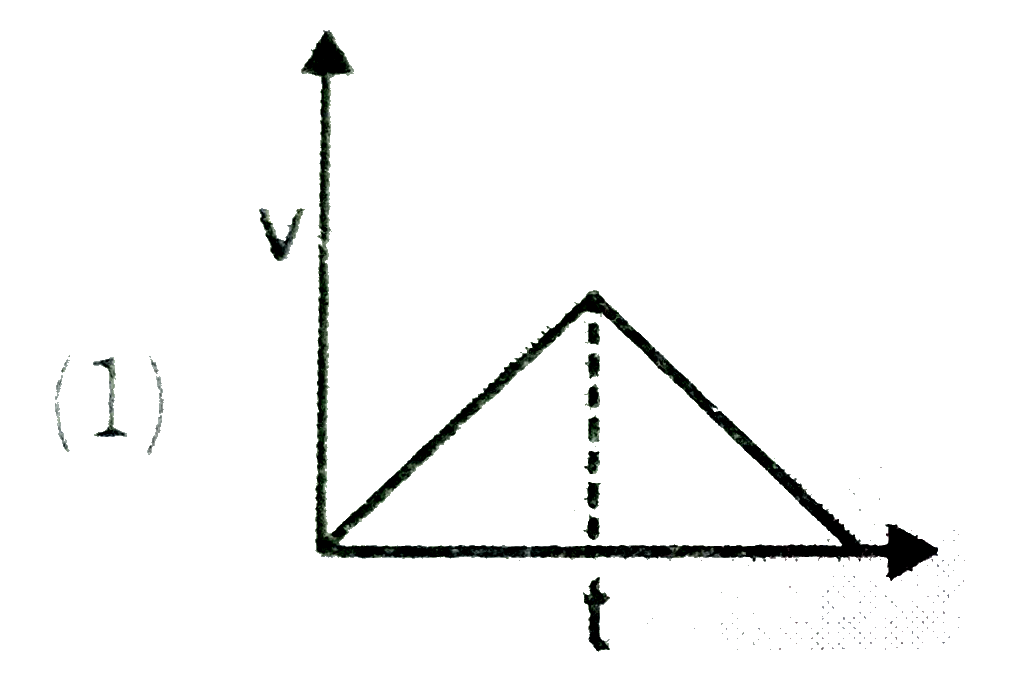 B
B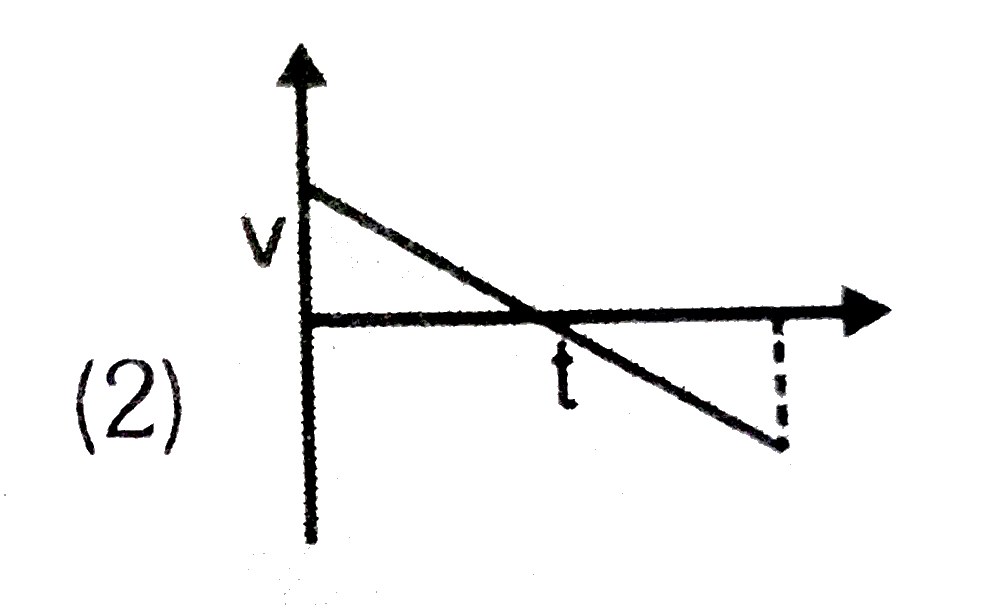 C
C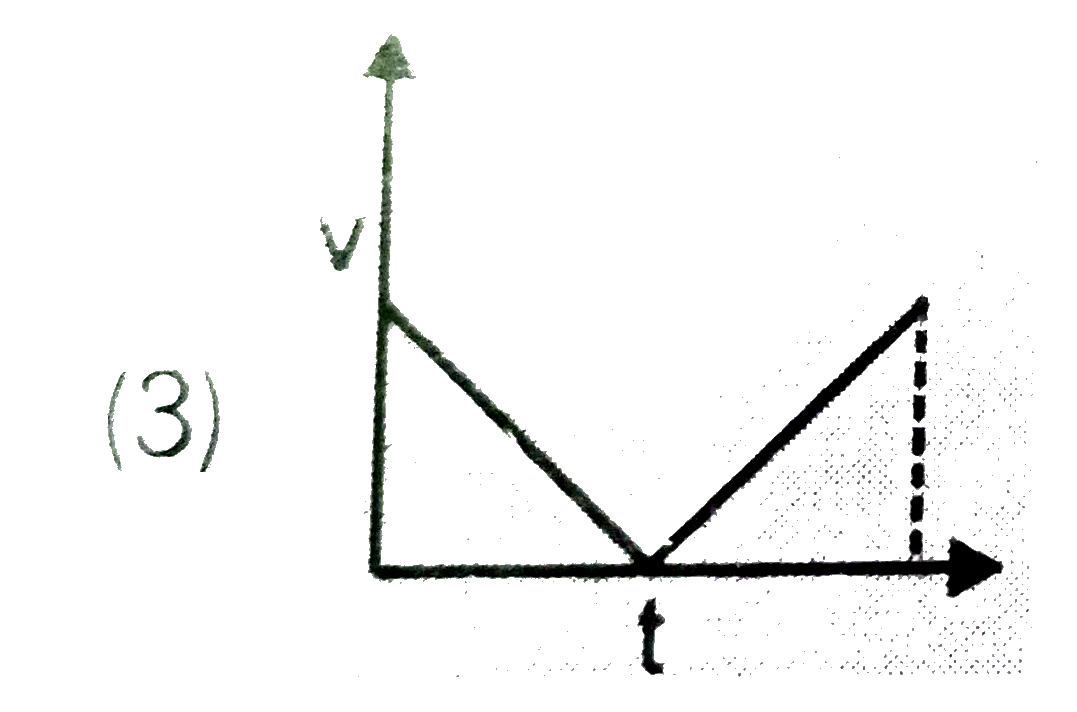 D
D
A body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to 1/3rd the escape velocity for the planet. The maximum height attained by the body is
AR/2BR/3CR/5DR/9
A body is projected vertically upwards from the earth's surface. The body reaches a height equal to one half of radius of earth. Calculate the initial speed with which the body was projected initially.
Radius of earth = 6,400 km
Mass of earth =6×1024kg
View SolutionA body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is Rn. Find the value of n.
View SolutionShow that if a body be projected vertically upward from the surface of the earth so as to reach a height nR above the surface
(i) the increase in its potential energy is (nn+1)mgR,
(ii) the velocity with it must be projected is √2ngRn+1, where r is the radius of the earth and m the mass of body.
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to hall the escape velocity for that planet. The maximum height attained by the body is
View SolutionA particle is throws vertically upwards from the surface of earth and it reaches to a maximum height equal to the radius of earth. The radio of the velocity of projection to the escape velocity on the surface of earth is
View Solution
