If a mercury drop is divided into 8 equal parts, its total energy,
remains same
becomes half
becomes twice
becomes 4 times
To solve the problem of finding the total energy of a mercury drop when it is divided into 8 equal parts, we will follow these steps:
Step 1: Understand the Initial Conditions
Let the radius of the original mercury drop be R. The volume of the original drop can be calculated using the formula for the volume of a sphere:
V=43πR3
Step 2: Calculate the Volume of Each Smaller Drop
When the original drop is divided into 8 equal parts, the volume of each smaller drop will be:
Vsmall=Voriginal8=18(43πR3)=16πR3
Step 3: Find the Radius of Each Smaller Drop
Let the radius of each smaller drop be r. The volume of a smaller drop can also be expressed as:
Vsmall=43πr3
Setting the two expressions for the volume equal gives:
43πr3=16πR3
Cancelling π and multiplying both sides by 6 gives:
8r3=R3⟹r3=R38⟹r=R2
Step 4: Calculate the Surface Area of the Original Drop
The surface area A of the original drop is given by:
Aoriginal=4πR2
Step 5: Calculate the Surface Area of All Smaller Drops
The surface area of one smaller drop is:
Asmall=4πr2=4π(R2)2=4πR24=πR2
The total surface area of the 8 smaller drops is:
Atotal=8×Asmall=8×πR2=8πR2
Step 6: Calculate the Change in Surface Area
The change in surface area when the drop is divided is:
ΔA=Atotal−Aoriginal=8πR2−4πR2=4πR2
Step 7: Calculate the Change in Surface Energy
The change in surface energy ΔU due to the change in surface area is given by:
ΔU=T⋅ΔA=T⋅(4πR2)
where T is the surface tension.
Step 8: Calculate the Total Energy
The initial surface energy Uinitial is:
Uinitial=T⋅Aoriginal=T⋅(4πR2)
The final surface energy Ufinal is:
Ufinal=T⋅Atotal=T⋅(8πR2)
Step 9: Determine the Ratio of Final to Initial Energy
The ratio of the final energy to the initial energy is:
UfinalUinitial=T⋅(8πR2)T⋅(4πR2)=84=2
Conclusion
Thus, when a mercury drop is divided into 8 equal parts, its total energy becomes twice the initial energy.
---
Let the radius of the original mercury drop be R. The volume of the original drop can be calculated using the formula for the volume of a sphere:
V=43πR3
When the original drop is divided into 8 equal parts, the volume of each smaller drop will be:
Vsmall=Voriginal8=18(43πR3)=16πR3
Let the radius of each smaller drop be r. The volume of a smaller drop can also be expressed as:
Vsmall=43πr3
Setting the two expressions for the volume equal gives:
43πr3=16πR3
Cancelling π and multiplying both sides by 6 gives:
8r3=R3⟹r3=R38⟹r=R2
The surface area A of the original drop is given by:
Aoriginal=4πR2
The surface area of one smaller drop is:
Asmall=4πr2=4π(R2)2=4πR24=πR2
The total surface area of the 8 smaller drops is:
Atotal=8×Asmall=8×πR2=8πR2
The change in surface area when the drop is divided is:
ΔA=Atotal−Aoriginal=8πR2−4πR2=4πR2
The change in surface energy ΔU due to the change in surface area is given by:
ΔU=T⋅ΔA=T⋅(4πR2)
where T is the surface tension.
The initial surface energy Uinitial is:
Uinitial=T⋅Aoriginal=T⋅(4πR2)
The final surface energy Ufinal is:
Ufinal=T⋅Atotal=T⋅(8πR2)
The ratio of the final energy to the initial energy is:
UfinalUinitial=T⋅(8πR2)T⋅(4πR2)=84=2
Thus, when a mercury drop is divided into 8 equal parts, its total energy becomes twice the initial energy.
Topper's Solved these Questions
- Mechanical Properties of fluidsBOOK - SL ARORACHAPTER - Mechanical Properties of fluidsEXERCISE - Exercise
459 Videos
- Mathematical toolsBOOK - SL ARORACHAPTER - Mathematical toolsEXERCISE - Exercise
20 Videos
- Mechanical Properties of SolidsBOOK - SL ARORACHAPTER - Mechanical Properties of SolidsEXERCISE - Example
113 Videos
Similar Questions
Knowledge Check
A water drop is divided into 8 equal droplets. The pressure difference between the inner and outer side of the big drop will be
Asame as for smaller dropletB12 of that for smaller dropletC14 of that for smaller dropletDtwice that for smaller dropletThe length of a string is 8 feet and 9 inches, which is divided into 3 equal parts. What is the length of each part in inches?
A31B33C35D37In a particular scale A, one metreis divided into 500equal parts and in scale B one cm is divided into 5 equal parts and in scale C one mm is divided into 2 equal parts, then the accuracy of ________.
AA>B>CBA=B<CCA=B>CDA=B=C
The spinner is divided into 8 equal parts. Find the probability of
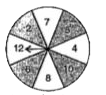
(i) Pointer lands on the shaded part
(ii) Pointer lands on a prime number
View SolutionIn a particular scale A, one metreis divided into 500equal parts and in scale B one cm is divided into 5 equal parts and in scale C one mm is divided into 2 equal parts, then the accuracy of ________.
View SolutionIn a particular scale A, one metreis divided into 500equal parts and in scale B one cm is divided into 5 equal parts and in scale C one mm is divided into 2 equal parts, then the accuracy of ________.
View SolutionA rectangle is divided horizontally into two equal parts. The upper part is further divided into three equal parts and the lower part is divided into four equal parts. Which fraction of the original rectangle is the shaded part ?
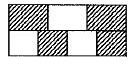
View SolutionA rectangle is divided horizontally into two equal parts. The upper part is further divided into three equal parts and the lower part is divided into four equal parts. Which fraction of the original rectangle is the shaded part?

View Solution
