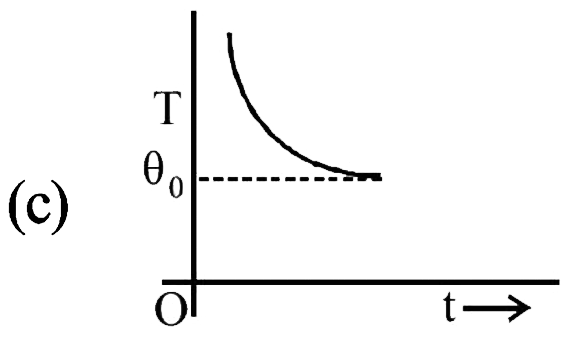
If a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to

The correct Answer is:C
To solve the problem, we need to analyze the cooling of a heated piece of metal according to Newton's Law of Cooling. Let's break down the steps:
1. Understanding the Problem:
- We have a piece of metal heated to a temperature θ.
- It is allowed to cool in a room at a constant temperature θ0.
- We need to determine the relationship between the temperature T of the metal and time t.
2. Applying Newton's Law of Cooling:
- According to Newton's Law of Cooling, the rate of change of temperature of the object is proportional to the difference between its temperature and the ambient temperature.
- Mathematically, this can be expressed as:
dθdt=−k(θ−θ0)
where k is a positive constant.
3. Rearranging the Equation:
- We can rearrange the equation to isolate the temperature terms:
dθθ−θ0=−kdt
4. Integrating Both Sides:
- We integrate both sides:
∫dθθ−θ0=−k∫dt
- This gives:
ln|θ−θ0|=−kt+C
where C is the integration constant.
5. Exponentiating to Solve for θ:
- To eliminate the logarithm, we exponentiate both sides:
|θ−θ0|=e−kt+C=eCe−kt
- Let A=eC, we can write:
θ−θ0=Ae−kt
6. Expressing θ:
- Thus, we can express the temperature θ as:
θ=θ0+Ae−kt
- Here, A is determined by the initial condition (the initial temperature of the metal).
7. Identifying the Graph:
- As time t increases, the term Ae−kt decreases exponentially, meaning that the temperature θ approaches θ0 asymptotically.
- The graph of θ versus t will show an exponential decay towards θ0.
8. Conclusion:
- The graph will be a curve that starts at θ and approaches θ0 over time, resembling an exponential decay function.
- Therefore, the correct answer is option C, which represents an exponential decrease.
- We have a piece of metal heated to a temperature θ.
- It is allowed to cool in a room at a constant temperature θ0.
- We need to determine the relationship between the temperature T of the metal and time t.
- According to Newton's Law of Cooling, the rate of change of temperature of the object is proportional to the difference between its temperature and the ambient temperature.
- Mathematically, this can be expressed as:
dθdt=−k(θ−θ0)
where k is a positive constant.
- We can rearrange the equation to isolate the temperature terms:
dθθ−θ0=−kdt
- We integrate both sides:
∫dθθ−θ0=−k∫dt
- This gives:
ln|θ−θ0|=−kt+C
where C is the integration constant.
- To eliminate the logarithm, we exponentiate both sides:
|θ−θ0|=e−kt+C=eCe−kt
- Let A=eC, we can write:
θ−θ0=Ae−kt
- Thus, we can express the temperature θ as:
θ=θ0+Ae−kt
- Here, A is determined by the initial condition (the initial temperature of the metal).
- As time t increases, the term Ae−kt decreases exponentially, meaning that the temperature θ approaches θ0 asymptotically.
- The graph of θ versus t will show an exponential decay towards θ0.
- The graph will be a curve that starts at θ and approaches θ0 over time, resembling an exponential decay function.
- Therefore, the correct answer is option C, which represents an exponential decrease.
Topper's Solved these Questions
Similar Questions
A sphere of radius r, density,ρ and specific heat s is heated to temperature θ and then cooled in an enclosure at temperature θ0 . How , the rate of fall of temperature is related with r, ρ and s?
View SolutionA piece of glass is heated to high temperature and then allowed to cool .If it cracks ,a possible reason for this is the following property of glass
View Solution
Knowledge Check
Which metal is a liquid at room temperature ?
AHgBKCNaDTiWhich metal is a liquid at room temperature?
AAluminiumBMercuryCCopperDBrassThe graph between the (velocity)2 and temperature T of a gas is
A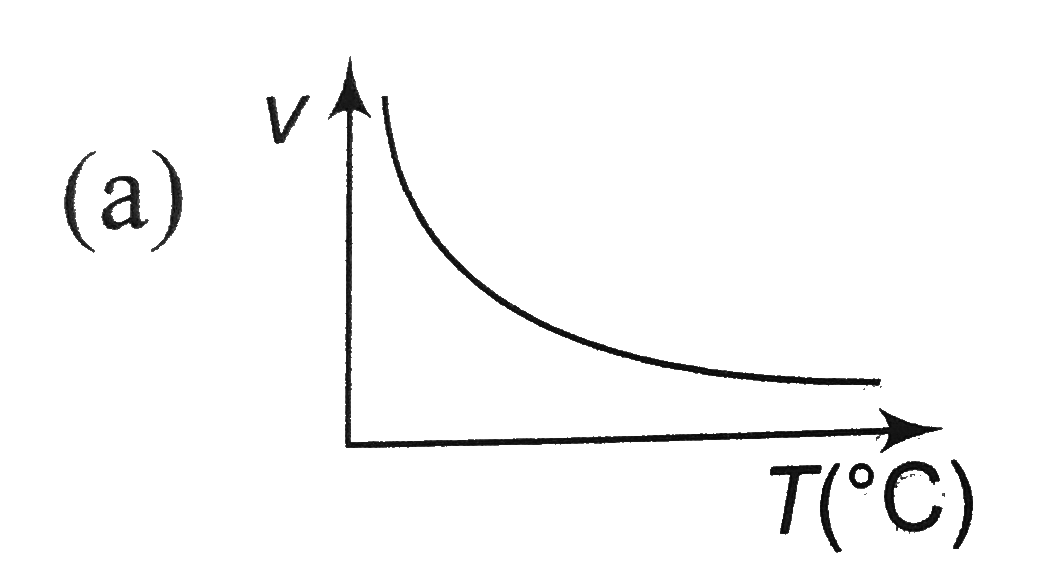 B
B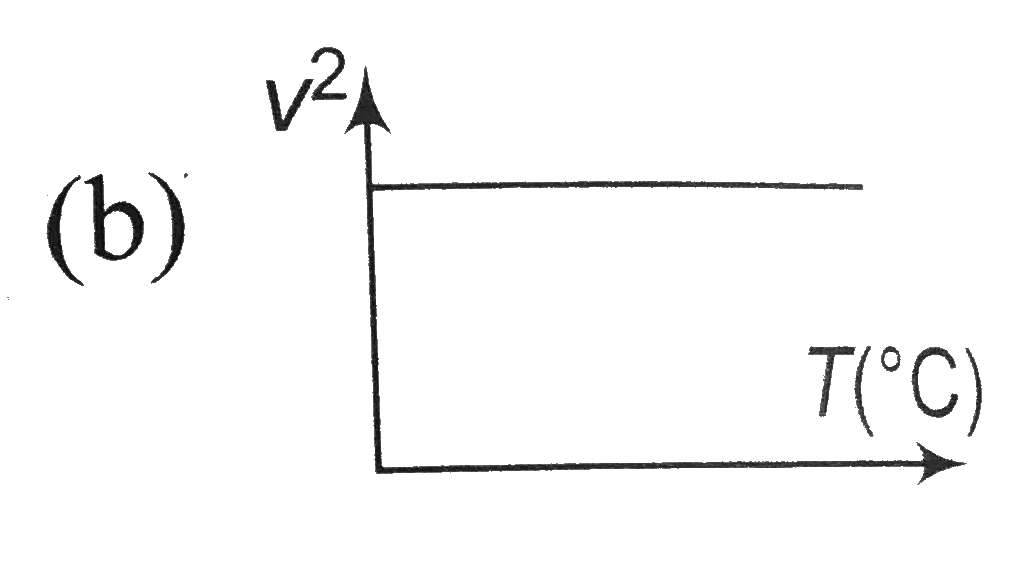 C
C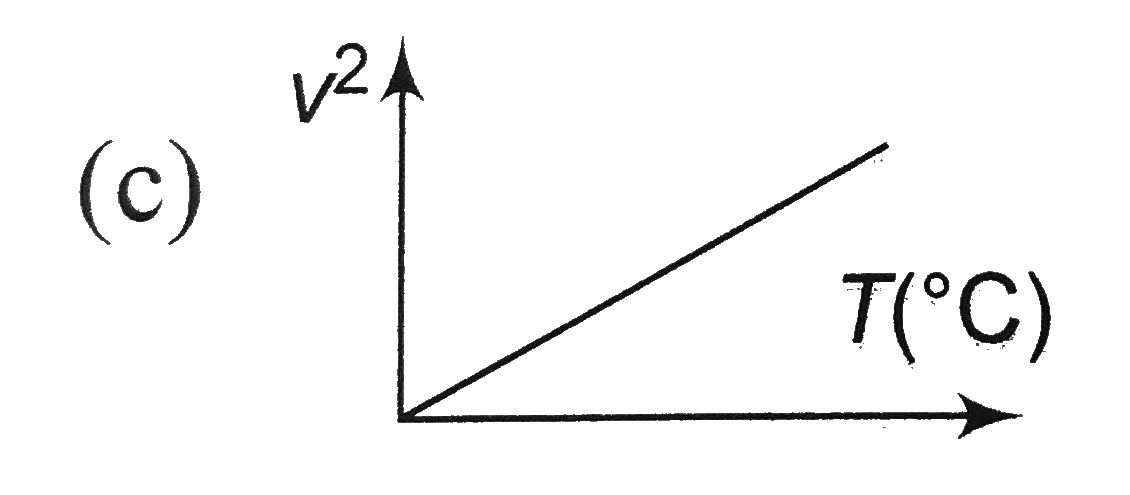 D
D
A piece of glass is heated to a high temperature and then allowed to cool. If it cracks, a probable reason for this is the following property of glass
View SolutionName a metal which is liquid at room temperature.
View SolutionA very thin metallic shell of radius r is heated to temperature T and then allowed to cool. The rate of cooling of shell is proportional to
View SolutionA non-metal which is gas at room temperature
View SolutionThe graph between surface tension and temperature T is
View Solution
