If a planet rotates too fast, rocks from its surface will start flying off its surface. If density of a homogeneous planet is ρand material is not flying off its surface then show that ts time period of rotation must be greater then √3πGp
To solve the problem, we need to establish a relationship between the time period of rotation of a planet and the conditions under which rocks do not fly off its surface due to centripetal force exceeding gravitational force.
1. Understanding Forces Acting on a Rock:
- When a planet rotates, a rock at its surface experiences two forces: gravitational force (mg) pulling it towards the center and centripetal force (Fc) due to the rotation.
- For a rock to remain on the surface, the gravitational force must be greater than or equal to the centripetal force.
2. Setting Up the Inequality:
- The condition for the rock not to fly off is given by:
Fc≤mg
- The centripetal force can be expressed as:
Fc=mω2r
- Where ω is the angular velocity, and r is the radius of the planet.
3. Substituting the Forces:
- Therefore, we have:
mω2r≤mg
- Dividing both sides by m (assuming m≠0):
ω2r≤g
- Rearranging gives:
ω2≤gr
4. Relating Angular Velocity to Time Period:
- The angular velocity ω is related to the time period T by:
ω=2πT
- Substituting this into the inequality gives:
(2πT)2≤gr
- This simplifies to:
4π2T2≤gr
5. Solving for Time Period T:
- Rearranging the inequality:
T2≥4π2rg
- Taking the square root of both sides:
T≥2π√rg
6. Expressing g in Terms of Density:
- The gravitational acceleration g at the surface of a planet can be expressed as:
g=GMr2
- The mass M of a homogeneous planet with density ρ can be expressed as:
M=ρ⋅V=ρ⋅43πr3
- Therefore:
g=G⋅ρ⋅43πr3r2=43Gρr
7. Substituting g Back:
- Substituting this expression for g back into the inequality for T:
T≥2π√r43Gρr=2π√34Gρ
8. Final Result:
- Simplifying gives:
T≥√3πGρ
- Thus, we have shown that the time period of rotation must be greater than √3πGρ.
- When a planet rotates, a rock at its surface experiences two forces: gravitational force (mg) pulling it towards the center and centripetal force (Fc) due to the rotation.
- For a rock to remain on the surface, the gravitational force must be greater than or equal to the centripetal force.
- The condition for the rock not to fly off is given by:
Fc≤mg
- The centripetal force can be expressed as:
Fc=mω2r
- Where ω is the angular velocity, and r is the radius of the planet.
- Therefore, we have:
mω2r≤mg
- Dividing both sides by m (assuming m≠0):
ω2r≤g
- Rearranging gives:
ω2≤gr
- The angular velocity ω is related to the time period T by:
ω=2πT
- Substituting this into the inequality gives:
(2πT)2≤gr
- This simplifies to:
4π2T2≤gr
- Rearranging the inequality:
T2≥4π2rg
- Taking the square root of both sides:
T≥2π√rg
- The gravitational acceleration g at the surface of a planet can be expressed as:
g=GMr2
- The mass M of a homogeneous planet with density ρ can be expressed as:
M=ρ⋅V=ρ⋅43πr3
- Therefore:
g=G⋅ρ⋅43πr3r2=43Gρr
- Substituting this expression for g back into the inequality for T:
T≥2π√r43Gρr=2π√34Gρ
- Simplifying gives:
T≥√3πGρ
- Thus, we have shown that the time period of rotation must be greater than √3πGρ.
Topper's Solved these Questions
Similar Questions
Show that the object lying at the equator will fly off the surface of earth, if the speed of rotation of the earth increase seventeen times its present speed.
View SolutionThe fastest possible of rotation of a planet is that for which the gravitational force on material at the equtor barely provides the centripetal force needed for the rotation. Show then that the corresponding shortest period of rotation is given by T=√3πGρ where ρ is the density of the planet, assumed to be homogeneous. Evalute the rotation period assuming a density of 3.0gm/cm2, typical of many planets, satellites, and asteroids. No such object is found to be spinning with a period shorter than found by this analysis.
View Solution
Knowledge Check
If the density of a planet is constant, then the curve between value of g on its surface and its radius r will be-
A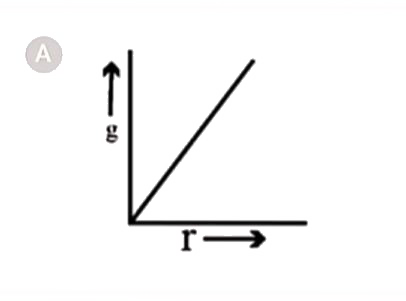 B
B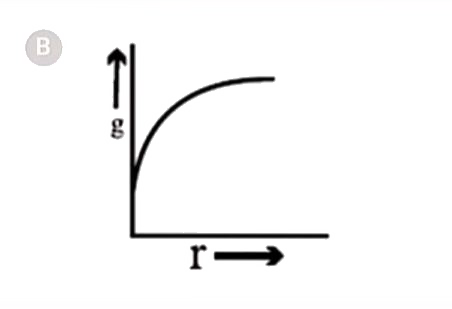 C
C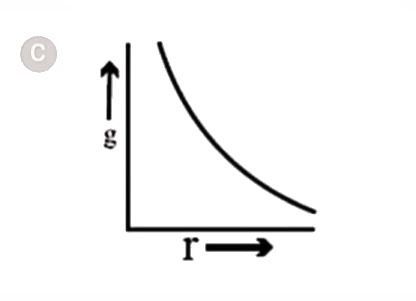 D
D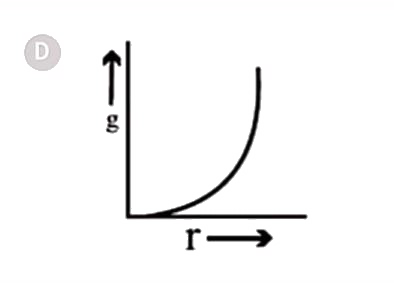
If the radius of a planet is R and its density is ρ , the escape velocity from its surface will be
Ave∝ρRBve∝√ρRCve∝√ρRDve∝1√ρRA body is projected from earth's surface to become its satellite, its time period of revolution will not depend upon
Amass of earthBits own massCgravitational constantDradius or orbit
A small satellite revolves round a planet in an orbit just above planet's surface. Taking the mean density of planet as ρ, calculate the time period of the satellite.
View SolutionWhat is the radius of a planet of density ρ if at its surface escape velocity of a body is v.
View SolutionIf a new planet is discovered rotating around Sun with the orbital radius double that of earth, then what will be its time period (in earth's days)
View SolutionThe escape velocity for a planet is ve. A particle is projected from its surface with a speed v. For this particle to move as a satellite around the planet.
View SolutionIf acceleration due to gravity on the surface of a planet is two times that on surface of earth and its radius is double that of earth. Then escape velocity from the surface of that planet in comparison to earth will be
View Solution
