If a thin uniform wire of length 1m is bent into an equilateral triangle and carries a current of √3A in anticlockwise direction, find the net magnetic induction at the centroid
To find the net magnetic induction at the centroid of an equilateral triangle formed by a wire carrying a current, we can follow these steps:
1. Determine the Length of Each Side of the Triangle:
Given that the total length of the wire is 1 meter and it is bent into an equilateral triangle, each side l of the triangle can be calculated as:
l=1 m3=13 m
2. Calculate the Distance from the Centroid to Each Side:
The distance d from the centroid to the midpoint of each side of the triangle is given by:
d=l2√3=132√3=16√3 m
3. Determine the Angles for the Magnetic Field Calculation:
In an equilateral triangle, the angles at each vertex are 60∘. Therefore, the angles we need for calculating the magnetic field contribution from each side are:
θ1=θ2=60∘
4. Calculate the Magnetic Field Contribution from One Side:
The magnetic field B′ at the centroid due to one side of the triangle can be calculated using the formula:
B′=μ0I4πd(sinθ1+sinθ2)
Substituting the values:
B′=μ0I4πd(sin60∘+sin60∘)=μ0I4πd⋅2⋅√32=μ0I√34πd
5. Calculate the Total Magnetic Field from All Three Sides:
Since there are three sides contributing equally to the magnetic field at the centroid, the total magnetic field B is:
B=3B′=3⋅μ0I√34πd=3μ0I√34πd
6. Substitute the Value of d:
Now substituting d=16√3:
B=3μ0I√34π(16√3)=3μ0I√3⋅6√34π=9μ0I4π
7. Substitute the Value of Current I:
Given I=√3 A:
B=9μ0√34π
8. Substitute the Value of μ0:
The permeability of free space μ0=4π×10−7T m/A:
B=9⋅(4π×10−7)⋅√34π=9⋅10−7√3T
9. Final Calculation:
Approximating √3≈1.732:
B≈9⋅1.732⋅10−7≈15.588×10−7T≈1.5588×10−6T
Final Answer:
The net magnetic induction at the centroid of the triangle is approximately:
B≈1.5588×10−6T
Given that the total length of the wire is 1 meter and it is bent into an equilateral triangle, each side l of the triangle can be calculated as:
l=1 m3=13 m
The distance d from the centroid to the midpoint of each side of the triangle is given by:
d=l2√3=132√3=16√3 m
In an equilateral triangle, the angles at each vertex are 60∘. Therefore, the angles we need for calculating the magnetic field contribution from each side are:
θ1=θ2=60∘
The magnetic field B′ at the centroid due to one side of the triangle can be calculated using the formula:
B′=μ0I4πd(sinθ1+sinθ2)
Substituting the values:
B′=μ0I4πd(sin60∘+sin60∘)=μ0I4πd⋅2⋅√32=μ0I√34πd
Since there are three sides contributing equally to the magnetic field at the centroid, the total magnetic field B is:
B=3B′=3⋅μ0I√34πd=3μ0I√34πd
Now substituting d=16√3:
B=3μ0I√34π(16√3)=3μ0I√3⋅6√34π=9μ0I4π
Given I=√3 A:
B=9μ0√34π
The permeability of free space μ0=4π×10−7T m/A:
B=9⋅(4π×10−7)⋅√34π=9⋅10−7√3T
Approximating √3≈1.732:
B≈9⋅1.732⋅10−7≈15.588×10−7T≈1.5588×10−6T
The net magnetic induction at the centroid of the triangle is approximately:
B≈1.5588×10−6T
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
A loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.
View SolutionA wire of length l is bent in the form of an equilateral triangle and carries an electric current i. (a) Find the magnetic field B at the centre. (b) If the wire is bent in the form of a square, what would be the value of B at the centre?
View SolutionA thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is :

View SolutionThe magnetic induction field at the centroid or an equilateral triangle of side 'I' and carrying a current 'i' is
View SolutionA thin wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction , as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper , the wire takes the shape of a circle . The tension in the wire is
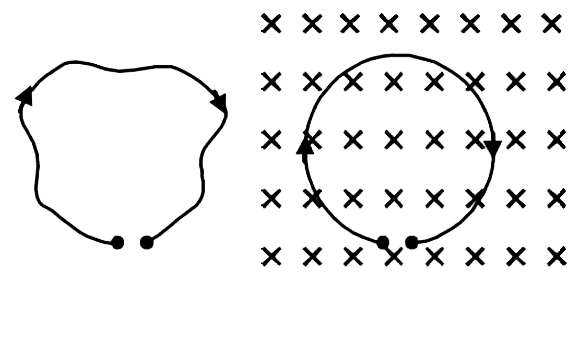
View SolutionA wire is bent in the form of an equilateral triangle of side 1m and carries a current of 2A.. It is placed in a magnetic field of induction 2.0 T directed into the plane of paper. The direction and magnitude of magnetic force acting on each side of the triangle will be
View Solution
A long wire bent as shown in the figure carries current I=10A. If the radius of the semicircular portion is 1 m, the magnetic induction (in μT) at the center C is
View SolutionA wire is bent in the form of an equilateral triangle PQR of side 10 cm and carries a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directed perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.
View SolutionA wire of length 'I' is bent into a circular loop of radius R and carries a current I. The magnetic field at the centre of the loop is 'B '. The same wire is now bent into a double loop. If both loops carry the same current I and it is in the same direction, the magnetic field at the centre of the double loop will be
View SolutionA circular coil of 200 mm diameter is made of 100 turns of thin wire and carries a current of 50 mA. Find the magnetic field induction at the centre of the coil.
View Solution
