The magnetic induction field at the centroid or an equilateral triangle of side 'I' and carrying a current 'i' is
2√2μ0iπl
9μ0i2πl
4μ0iπl
3√3μ0iπl
The correct Answer is:B
To find the magnetic induction field at the centroid of an equilateral triangle of side 'l' carrying a current 'i', we can follow these steps:
1. Identify the Geometry:
- We have an equilateral triangle with each side of length 'l'.
- The centroid (O) of the triangle is the point where we want to calculate the magnetic field.
2. Determine the Height of the Triangle:
- The height (h) of an equilateral triangle can be calculated using the formula:
h=√32l
3. Calculate the Perpendicular Distance from the Centroid to a Side:
- The perpendicular distance (r) from the centroid to any side of the triangle is given by:
r=13h=13(√32l)=l2√3
4. Determine the Angles:
- The angle subtended by the current-carrying side at the centroid is 60 degrees for each side.
5. Apply Biot-Savart Law:
- According to the Biot-Savart Law, the magnetic field (B) due to a straight current-carrying wire at a distance 'r' is given by:
B=μ04π⋅ir⋅(sinθ1+sinθ2)
- For each side of the triangle, since both angles (θ1 and θ2) are 60 degrees:
B=μ04π⋅ir⋅(sin60+sin60)=μ04π⋅ir⋅(2⋅sin60)
6. Substituting Values:
- Substitute r=l2√3 and sin60=√32:
B=μ04π⋅il2√3⋅(2⋅√32)
- Simplifying gives:
B=μ04π⋅i⋅2√3l⋅√32=μ0⋅3i4πl
7. Total Magnetic Field from All Sides:
- Since there are three sides contributing to the magnetic field, the total magnetic field (B_total) at the centroid is:
Btotal=3B=3⋅μ0⋅3i4πl=9μ0i4πl
8. Final Result:
- The magnetic induction field at the centroid of the equilateral triangle is:
B=9μ0i4πl
- We have an equilateral triangle with each side of length 'l'.
- The centroid (O) of the triangle is the point where we want to calculate the magnetic field.
- The height (h) of an equilateral triangle can be calculated using the formula:
h=√32l
- The perpendicular distance (r) from the centroid to any side of the triangle is given by:
r=13h=13(√32l)=l2√3
- The angle subtended by the current-carrying side at the centroid is 60 degrees for each side.
- According to the Biot-Savart Law, the magnetic field (B) due to a straight current-carrying wire at a distance 'r' is given by:
B=μ04π⋅ir⋅(sinθ1+sinθ2)
- For each side of the triangle, since both angles (θ1 and θ2) are 60 degrees:
B=μ04π⋅ir⋅(sin60+sin60)=μ04π⋅ir⋅(2⋅sin60)
- Substitute r=l2√3 and sin60=√32:
B=μ04π⋅il2√3⋅(2⋅√32)
- Simplifying gives:
B=μ04π⋅i⋅2√3l⋅√32=μ0⋅3i4πl
- Since there are three sides contributing to the magnetic field, the total magnetic field (B_total) at the centroid is:
Btotal=3B=3⋅μ0⋅3i4πl=9μ0i4πl
- The magnetic induction field at the centroid of the equilateral triangle is:
B=9μ0i4πl
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-III
49 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
View SolutionFind the magnetic field B at the centre of a rectangular loop of length l and width b, carrying a current i.
View SolutionThe electric field at the centroid of an equilateral triangle carrying an equal charge q at each of the vertices is :
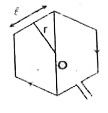
View SolutionThe magnetic field at centre of a hexagonal coil of side l carrying a current I is
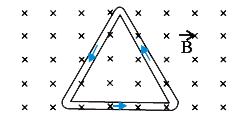
View SolutionA wire is bent in the form of an equilateral triangle of side 1m and carries a current of 2A.. It is placed in a magnetic field of induction 2.0 T directed into the plane of paper. The direction and magnitude of magnetic force acting on each side of the triangle will be
View SolutionA wire is bent in the form of an equilateral triangle PQR of side 10 cm and carries a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directed perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.
View SolutionThe magnetic field at the point of intersection of diagonals of a square wire loop of side L, carrying a current I is
View SolutionMagnetic field at the centre of regular hexagon current carrying loop of side length l and current i is
View SolutionMagnitude of magnetic field (in SI units) at the centre of a hexagonal shape coil of side 10cm , 50 turns and carrying current I (Ampere) in units of μ0Iπ is :
View SolutionThree parallel long straight conductors are carrying equal currents i each as shown. Th e conductors are passing tlrrough the vertices of equilateral triangle of side 'a'.

Find the magnetic firld at C the centroid of triangle
View Solution
