If a wave y(x,t)=(5.0 mm) sin(kr +(600 rad/s) $t + ϕ)$ travels along a string, how much time does any given point on the string take to move between displacements y=+2.0 mm and y=-2.0 mm?

Video Solution

Text Solution

Generated By DoubtnutGPT

The correct Answer is:0.0014 s or 1.4ms

To solve the problem of how much time a given point on the string takes to move between displacements $y = + 2.0 mm$ and $y = - 2.0 mm$ , we can follow these steps:
Step 1: Understand the wave equation
The wave is given by:
$y (x, t) = (5.0 mm) sin (k x + (600 rad/s) t + ϕ)$
Here, $A = 5.0 mm$ , $ω = 600 rad/s$ , and $k$ is the wave number.
Step 2: Set up equations for displacements
To find the times $t_{1}$ and $t_{2}$ when the displacement is $+ 2.0 mm$ and $- 2.0 mm$ , we set up the following equations:
1. For $y = + 2.0 mm$ :
$5.0 sin (k x + 600 t_{1} + ϕ) = 2.0$
Simplifying gives:
$sin (k x + 600 t_{1} + ϕ) = \frac{2.0}{5.0} = \frac{2}{5} = 0.4$
2. For $y = - 2.0 mm$ :
$5.0 sin (k x + 600 t_{2} + ϕ) = - 2.0$
Simplifying gives:
$sin (k x + 600 t_{2} + ϕ) = - \frac{2.0}{5.0} = - 0.4$
Step 3: Use inverse sine to find angles
Now we can find the angles corresponding to these sine values:
1. For $t_{1}$ :
$k x + 600 t_{1} + ϕ = {sin}^{- 1} (0.4)$
Let $θ_{1} = {sin}^{- 1} (0.4)$ .
2. For $t_{2}$ :
$k x + 600 t_{2} + ϕ = {sin}^{- 1} (- 0.4)$
Let $θ_{2} = {sin}^{- 1} (- 0.4)$ .
Step 4: Find the time difference
Now, we can subtract the two equations:
$600 t_{1} - 600 t_{2} = θ_{1} - θ_{2}$
This simplifies to:
$600 (t_{1} - t_{2}) = θ_{1} - θ_{2}$
Thus, we can express the time difference as:
$t_{1} - t_{2} = \frac{θ_{1} - θ_{2}}{600}$
Step 5: Calculate the angles
Using the properties of sine:
- $θ_{1} = {sin}^{- 1} (0.4)$
- $θ_{2} = - {sin}^{- 1} (0.4)$
So:
$θ_{1} - θ_{2} = {sin}^{- 1} (0.4) - (- {sin}^{- 1} (0.4)) = 2 {sin}^{- 1} (0.4)$
Step 6: Substitute and calculate time
Substituting back into the equation for time:
$t_{1} - t_{2} = \frac{2 {sin}^{- 1} (0.4)}{600}$
Step 7: Calculate ${sin}^{- 1} (0.4)$
Using a calculator:
${sin}^{- 1} (0.4) \approx 0.4115 radians$
Thus:
$t_{1} - t_{2} = \frac{2 \times 0.4115}{600} \approx \frac{0.823}{600} \approx 0.001372 s \approx 1.37 ms$
Final Answer
The time taken for any given point on the string to move between displacements $y = + 2.0 mm$ and $y = - 2.0 mm$ is approximately $1.37 ms$ .
---

Updated on:18/9/2024

Class 12 PHYSICS TRAVELLING WAVES

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the $x$ - direction and displacements of elements on the string are along the $y$ - direction . Individual equations of the two waves can be expressed as
$Y_{1} = 6 (c m) sin [5 (r a d / c m) x - 4 (r a d / s) t]$
$Y_{2} = 6 (c m) sin [5 (r a d / c m) x + 4 (r a d / s) t]$ Here $x$ and $y$ are in $c m$ .
Answer the following questions.
If one end of the string is at $x = 0$ , positions of the nodes can be described as
A $x = n π / 5 c m, w h e r e n = 0, 1, 2, \dots$
B $x = n 2 π / 5 c m, w h e r e n = 0, 1, 2, \dots$
C $x = n π / 5 c m, w h e r e n = 0, 1, 3, 5, \dots$
D $x = n π / 10 c m, w h e r e n = 0, 1, 3, 5, \dots$
Question 2 - Select One
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the $x$ - direction and displacements of elements on the string are along the $y$ - direction . Individual equations of the two waves can be expressed as
$Y_{1} = 6 (c m) sin [5 (r a d / c m) x - 4 (r a d / s) t]$
$Y_{2} = 6 (c m) sin [5 (r a d / c m) x + 4 (r a d / s) t]$ Here $x$ and $y$ are in $c m$ .
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at $t = 0$ due to superposition of waves given by $y_{1}$ and $y_{2}$ in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , $N$ is a node and $A$ and antinode . At this instant say $t = 0$ , instantaneous velocity of points on the string

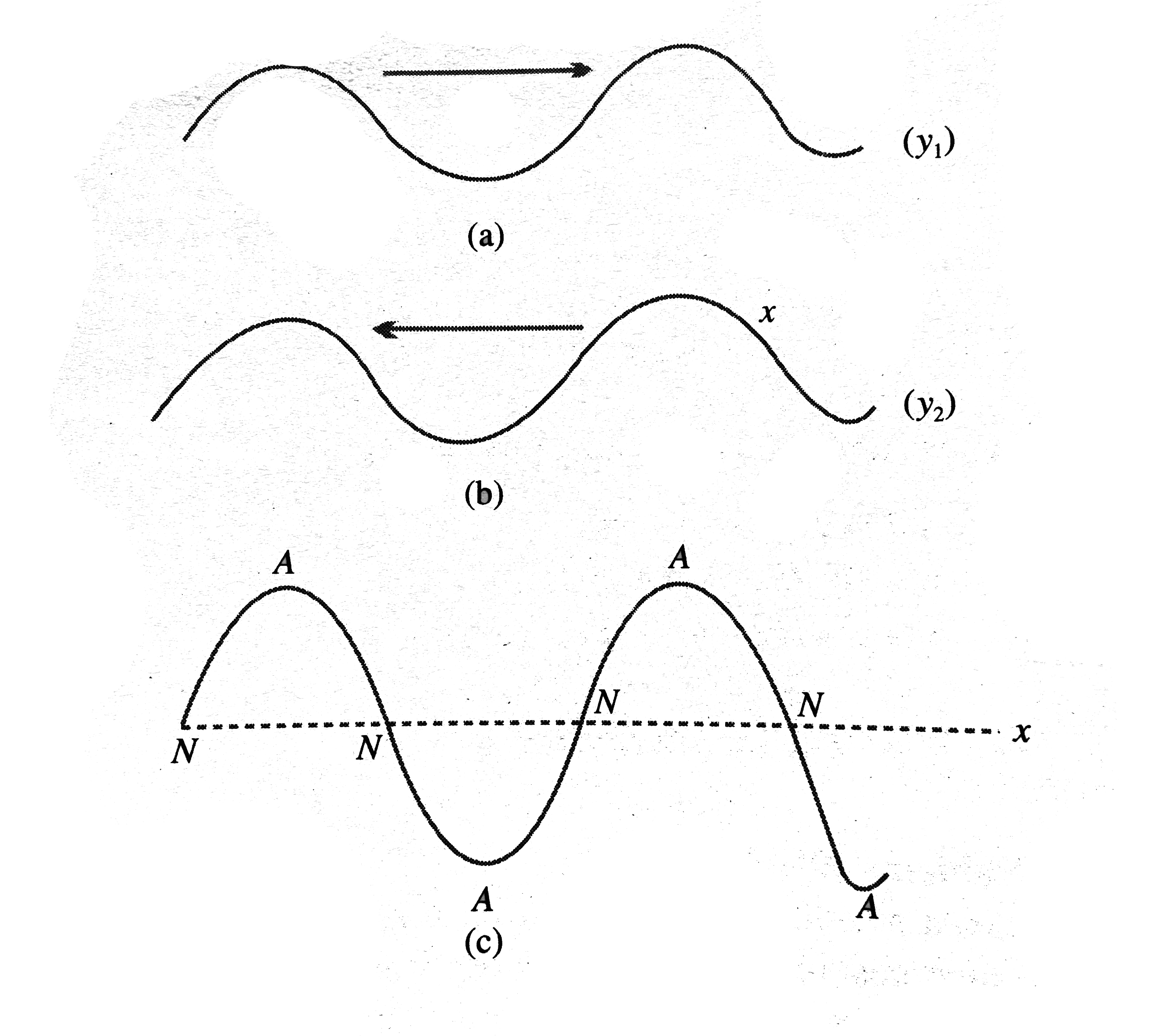Ais different for different points
Bis zero for all points
Cchanges with position of the point
Dis constant but not equal to zero for all points
Question 3 - Select One
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the $x$ - direction and displacements of elements on the string are along the $y$ - direction . Individual equations of the two waves can be expressed as
$Y_{1} = 6 (c m) sin [5 (r a d / c m) x - 4 (r a d / s) t]$
$Y_{2} = 6 (c m) sin [5 (r a d / c m) x + 4 (r a d / s) t]$ Here $x$ and $y$ are in $c m$ .
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at $x = 1.8 c m$ will be
A $3.3 c m$
B $6.7 c m$
C $4.9 c m$
D $2.6 c m$

RESNICK AND HALLIDAY-WAVES-I-Problems

Home
Ask Doubt
Profile

If a wave y(x,t)=(5.0 mm) sin(kr +(600 rad/s) t+ϕ) travels along a string, how much time does any given point on the string take to move between displacements y=+2.0 mm and y=-2.0 mm?

The correct Answer is:0.0014 s or 1.4ms

Topper's Solved these Questions

Similar Questions

Knowledge Check

RESNICK AND HALLIDAY-WAVES-I-Problems

If a wave y(x,t)=(5.0 mm) sin(kr +(600 rad/s) $t + ϕ)$ travels along a string, how much time does any given point on the string take to move between displacements y=+2.0 mm and y=-2.0 mm?