If a wire of length 4 m and cross-sectional area of 2m2 is stretched by a force of 3 kN, then determine the change in length due to this force . Given, Young's modulus of material of wire is 110×109Nm−2
To determine the change in length of the wire when a force is applied, we can use the formula related to Young's modulus:
Y=F⋅LA⋅ΔL
Where:
- Y is Young's modulus,
- F is the applied force,
- L is the original length of the wire,
- A is the cross-sectional area,
- ΔL is the change in length.
We can rearrange this formula to solve for the change in length (ΔL):
ΔL=F⋅LA⋅Y
Step 1: Identify the given values
- Length of the wire, L=4m
- Cross-sectional area, A=2m2
- Force applied, F=3kN=3×103N
- Young's modulus, Y=110×109N/m2
Step 2: Substitute the values into the formula
Now, we substitute the values into the rearranged formula:
ΔL=(3×103N)⋅(4m)(2m2)⋅(110×109N/m2)
Step 3: Calculate the numerator
Calculate the numerator:
3×103N⋅4m=12×103N m=1.2×104N m
Step 4: Calculate the denominator
Calculate the denominator:
2m2⋅110×109N/m2=220×109N
Step 5: Divide the numerator by the denominator
Now, we divide the numerator by the denominator:
ΔL=1.2×104N m220×109N=1.2220×10−5m
Step 6: Simplify the fraction
Now, simplifying the fraction:
ΔL=1.2220≈0.005454545×10−5m
Step 7: Convert to micrometers
Convert this value to micrometers (1 m = 106μm):
ΔL≈54.5×10−6m=54.5μm
Final Answer
The change in length due to the applied force is approximately:
ΔL≈54.5μm
- Y is Young's modulus,
- F is the applied force,
- L is the original length of the wire,
- A is the cross-sectional area,
- ΔL is the change in length.
- Length of the wire, L=4m
- Cross-sectional area, A=2m2
- Force applied, F=3kN=3×103N
- Young's modulus, Y=110×109N/m2
Now, we substitute the values into the rearranged formula:
Calculate the numerator:
Calculate the denominator:
Now, we divide the numerator by the denominator:
Now, simplifying the fraction:
Convert this value to micrometers (1 m = 106μm):
The change in length due to the applied force is approximately:
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Solved Examples
6 Videos
- ELASTICITYBOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - MiscellaneousExamples
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
469 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A uniform wire of length 6m and a cross-sectional area 1.2 cm2 is stretched by a force of 600N . If the Young's modulus of the material of the wire 20×1010Nm−2 , calculate (i) stress (ii) strain and (iii) increase in length of the wire.
View Solution(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.
View Solution
Knowledge Check
A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAlA wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2L
The area of cross - section of a wire is 1 mm2 and it length is 2 m. How much work will be done to increase its length by 0.1 mm ? The Young.s modulus of elaticity for the material of the wire is 2×1011 Nm−2.
View SolutionA wire one square centimeter area of cross-section is stretched by a force to double its original length. Calculate the force. Young's modulus = 90 GPa. Assume that the wire does not break.
View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View Solution(a) A wire 4 m long and 0.3mm in diameter is stretched by a force of 100 N. If extension in the wire is 0.3 mm, calculate the potential energy stored in the wire.
(b) Find the work done is stretching a wire of cross-section 1mm2 and length 2 m through 0.1 mm. Young's modulus for the material of wire is 2.0×1011Nm−2.
View SolutionA wire of length l, area of cross section A and Young’s modulus of elasticity Y is stretched by a longitudinal force F. The change in length is Δl Match the following two columns.
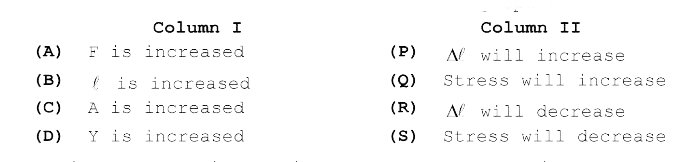
View SolutionFind the work done in stretching a wire Im long and area of cross section 0.03 cm under a load of 100 N if Young.s modulus of the material of the wire is 2×1011N/m2
View Solution
