An indian ruber cord L meter long and area of cross-secion A metre is suspended vertically. Density of rubber is ρ kg/ metre3 and Young's modulus of rubber is Y newton/ metre2. IF the cord extends by l metre under its own. Weight, then extension l is
L2Dg2E
L2DgE
L2Dg4E
L
The correct Answer is:A
(a) Volume of the rubber cord=AL
Weight of the rubber cord =ALDg.
∴ Stress=ALDgA=LDg
The weight of the rubber cord acts at the centre of gravity which is L2 from the top.
∴ Strain =lL/2=2lL
So, Young's modulus, E=StressStrain=LDg2l/L=L2Dg2l
or l=L2Dg2E
Topper's Solved these Questions
Similar Questions
An indian ruber cord L meter long and area of cross-secion A metre is suspended vertically. Density of rubber is ρ kg/ metre3 and Young's modulus of rubber is Y newton/ metre2. IF the cord extends by l metre under its own. Weight, then extension l is
View SolutionA rubber cord of density d, Young's modulus Y and length L is suspended vertically . If the cord extends by a length 0.5 L under its own weight , then L is
View SolutionA thin rod of negligible mass and area of cross section S is suspended vertically from one end. Length of the rod is L0 at T∘C . A mass m is attached to the lower end of the rod so that when temperature of the rod is reduced to 0∘C its length remains L0 Y is the Young’s modulus of the rod and α is coefficient of linear expansion of rod. Value of m is :
View SolutionA rubber cord 10m long is suspended vertically. How much does it stretch under its own weight (Density of rubber is 1500kg/m,Y=5×10N/m,g=10m/s)
View SolutionA wire of length l and cross-sectional are A is suspended at one of its ends from a ceiling. What will be its strain energy due to its own weight, if the density and Young's modulus of the material of the wire be d and Y?
View SolutionA heavy rope is suspended from the ceiling of a room. If ϕ is the density of the rope, L be its original length and Y be its. Young's modulus, then increase ΔL in the length of the rope due to its own weight is
View Solutionwire of length I has a ear mass density λ and area of cross-section A and the Young's modulus y is suspended vertically from rigid support. The extension produced in wire due to its own weight
View SolutionA wire havinga length L and cross- sectional area A is suspended at one of its ends from a ceiling . Density and young's modulus of material of the wire are ρ and Y, respectively. Its strain energy due to its own weight is ρ2g2AL3αY. Find the vqalue of α
View SolutionA uniform rod of length 2L, area of cross - section A and Young's modulus Y is lying at rest under the action of three forces as shown.
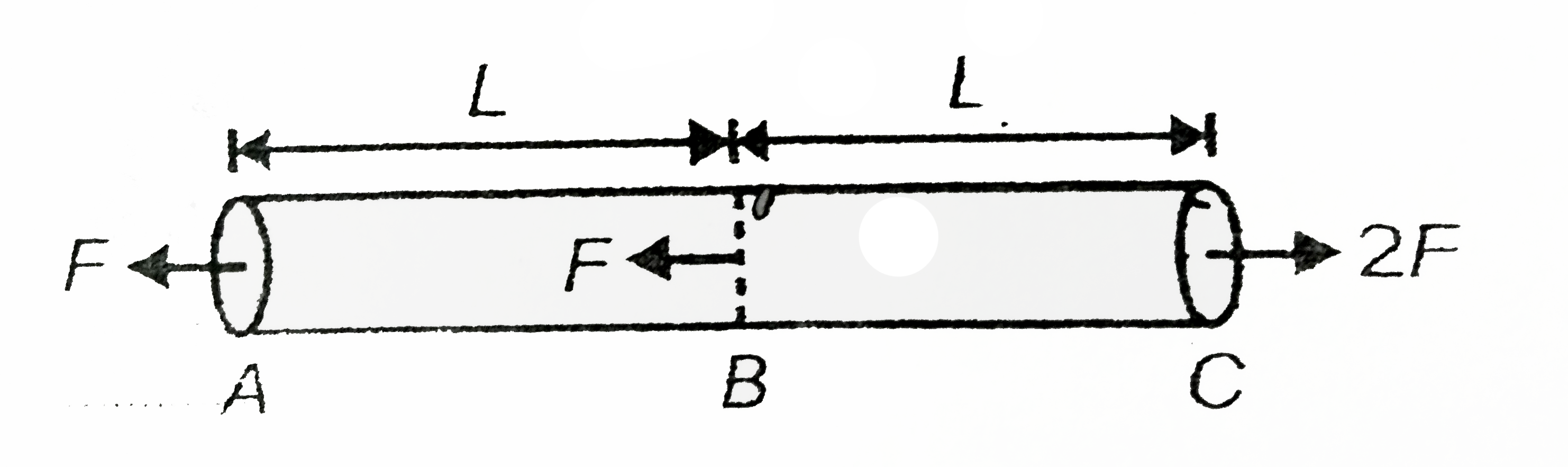
Select the correct alternatives.View SolutionFind the increment in the length of a steel wire of length 5m and radius 6mm under its own weight. Density of steel =8000kg/m3 and young's modulus of steel =2×1011N/m2. What is the energy stored in the wire ? (Take g =9.8m/s2)
View Solution

