If α=2N0λ, calculate the number of nuclei of A after one half-life of A, and also the limiting value of N as
2N0,52N0
3N0,2N0
4N0,2N0
32N0,2N0
The correct Answer is:d
If α=2λN0, t=half life =In(2)λ
∴N=1λ[2λN0−(2λN0−λN0)e−λt]
or N=λN0λ[2−eIn(2)][Here e−In(2)=2−1=12]
or N=λN0λ[2−12]=3N02 or N=32N0
When t→∞ and α=2λN0
N=αλ=2λN0λ=2N0 or N=2N0
Topper's Solved these Questions
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - EXEMPLAR PROBLEMS
7 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - ASSERTION & REASON
15 Videos
- NUCLEIBOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason
15 Videos
- MOVING CHARGES AND MAGNETISM BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Assertion And Reason
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
Similar Questions
Nuclei of radioactive element A are being produced at a constant rate. α. The element has a decay constant λ. At time t=0, there are N0 nuclei of the element.
(a) Calculate the number N of nuclei of A at time t.
(b) IF α=2N0λ , calculate the number of nuclei of A after one half-life time of A and also the limiting value of N at t→∞.
View SolutionNuclei of a radioactive A are being produceted at a constant rate a . The electro has a decay constant λ . At time t=0 there are N0nucleius of the element .
(a) calculate the number N of nuclei of A at same t
(b) if a = 2N_(0) lambda) calca––tetheνmberofνc≤iofAaftero≠half−lifeofAandthelimit∈gvalueofNast rarr oo
View Solution
Knowledge Check
Nuclei of a radioactive element 'A' are being produced at a constant rate, α . The element has a decay constant, λ. At time, t = 0, there are N0 nuclei of the element.
If α=2N0λ the number of nuclei of A after one half life of A becomesAzeroB2N0C1.5N0D0.5N0Nuclei of a radioactive element 'A' are being produced at a constant rate α the element has a decay constant λ At time t=0 there are N0 nuclei of the element
If α=2N0λ the number of nuclei of A after undergone radioactivity decay till time t=ln2λ:A0.5N0B1.5N0C(4ln2−1)N02D(4ln2−3)N02Consider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.
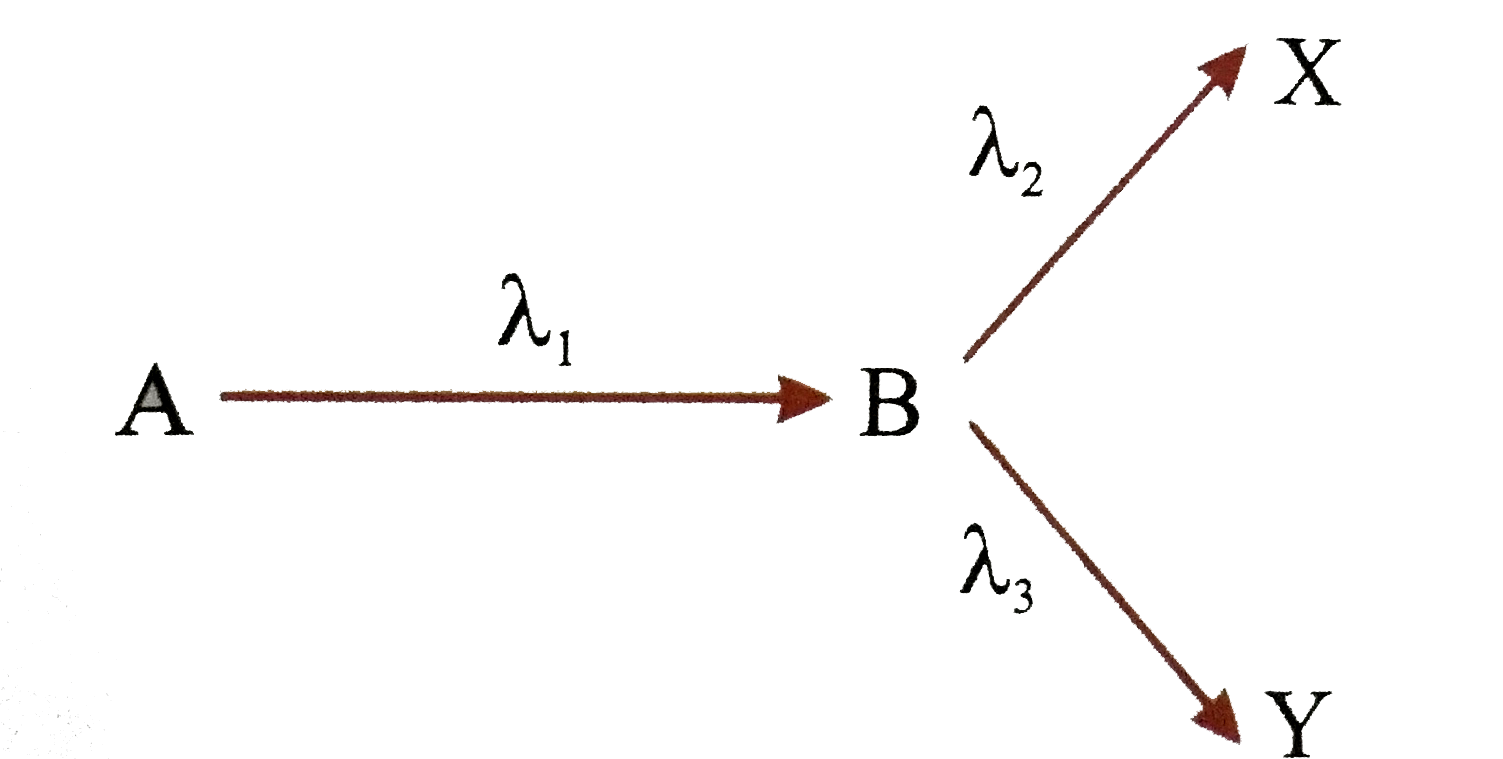
The number of nuclei of B will first increase and then after a maximum value, it decreases forAλ1>λ2+λ3Bλ1=λ2=λ3Cλ1=λ2+λ3DFor any values of λ1,λ2 and λ3
A sample contains two isotopes -one stale and the other unstable. Number of stable nuclei is equal to Ns and number of unstable nuclei is equal to Nu. After a time the activity of the sample decreased to one thrid of the, the initial activity while the total number of nuclei (excluding decayed nuclei) became half. find the initial value of the ratio Ns/Nu.
View SolutionA stable nuclei C is formed from two radioactive nuclei A and B with decay constant of λ1 and λ2 respectively. Initially, the number of nuclei of A is N0 and that of B is zero. Nuclei B are produced at a constant rate of P. Find the number of the nuclei of C after time t.
View SolutionA stable nuclei C is formed from two radioactive nuclei A and B with decay constant of λ1 and λ2 respectively. Initially, the number of nuclei of A is N0 and that of B is zero. Nuclei B are produced at a constant rate of P. Find the number of the nuclei of C after time t.
View SolutionConsider radioactive decay of A to B with which further decays either to X or Y, λ1,λ2 and λ3 are decay constant for A to B decay, B to X decay and Bto Y decay respectively. At t=0, the number of nuclei of A,B,X and Y are N0,N0 zero and zero respectively.
N1,N2,N3 and N4 are the number of nuclei of A,B,X and Y at any instant t.

The number of nuclei of B will first increase and then after a maximum value, it decreases for
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate α the element has a decay constant λ At time t=0 there are N0 nuclei of the element
If α=2N0λ the number of nuclei of A after t=ln2λ will become:
View Solution
