If Bohr's qunatisation postulate (angular momentum=nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do never speak of quantization of orbits of planets around the sun?
To understand why we do not speak of the quantization of orbits of planets around the sun, we can analyze the situation step by step.
1. Understanding Bohr's Quantization Postulate:
Bohr's quantization postulate states that the angular momentum of an electron in an atom is quantized and is given by the formula L=nh2π, where n is a positive integer (quantum number) and h is Planck's constant.
2. Application to Planetary Motion:
If we were to apply this postulate to planetary motion, we would consider the angular momentum of a planet orbiting the sun. The angular momentum L for a planet can be expressed as L=mvr, where m is the mass of the planet, v is its orbital velocity, and r is the radius of the orbit.
3. Magnitude of Angular Momentum in Planetary Motion:
For planets, the angular momentum is extremely large. For example, the angular momentum of Earth in its orbit is approximately 1070ℏ (where ℏ=h2π). This is a significantly large value compared to atomic scales.
4. Quantization Levels:
In quantum mechanics, quantization leads to discrete energy levels. However, when the values of n (quantum number) are large, the difference between successive energy levels becomes very small. As a result, these levels can be considered continuous rather than discrete.
5. Conclusion:
Due to the extremely large angular momentum values associated with planetary motion, the differences in energy levels become negligible. Thus, for practical purposes, we treat planetary orbits as continuous rather than quantized. This is why we do not speak of the quantization of orbits of planets around the sun.
Bohr's quantization postulate states that the angular momentum of an electron in an atom is quantized and is given by the formula L=nh2π, where n is a positive integer (quantum number) and h is Planck's constant.
If we were to apply this postulate to planetary motion, we would consider the angular momentum of a planet orbiting the sun. The angular momentum L for a planet can be expressed as L=mvr, where m is the mass of the planet, v is its orbital velocity, and r is the radius of the orbit.
For planets, the angular momentum is extremely large. For example, the angular momentum of Earth in its orbit is approximately 1070ℏ (where ℏ=h2π). This is a significantly large value compared to atomic scales.
In quantum mechanics, quantization leads to discrete energy levels. However, when the values of n (quantum number) are large, the difference between successive energy levels becomes very small. As a result, these levels can be considered continuous rather than discrete.
Due to the extremely large angular momentum values associated with planetary motion, the differences in energy levels become negligible. Thus, for practical purposes, we treat planetary orbits as continuous rather than quantized. This is why we do not speak of the quantization of orbits of planets around the sun.
Topper's Solved these Questions
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - very short question 2
2 Videos
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - very short question 3
2 Videos
- ATOMS AND NUCLEIBOOK - PRADEEPCHAPTER - ATOMS AND NUCLEIEXERCISE - Additional Exercise question 4
1 Videos
- COMMUNICATION SYSTEMSBOOK - PRADEEPCHAPTER - COMMUNICATION SYSTEMSEXERCISE - MODEL TEST PAPER-2
9 Videos
Similar Questions
If Bohr's qunatisation postulate (angular momentum=nh/2π) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do never speak of quantization of orbits of planets around the sun?
View SolutionIf Bohr’s quantization postulate (angular momentum = nh/2π ) is a basic law of nature, it should be equally valid for the case of planetary motion also. Why then do we never speak of quantization of orbits of planets around the sun?
View Solution
Knowledge Check
In a hydrogen like ion, nucleus has a positive charge Ze, Bohr's quantization rule is, the angular momentum of an electron about the nucleus l=nh2π, where 'n' is a positive integer.
If electron is in ground state the magnetic field produced at the site of nucleus due to circular motion of the electronAμ0Z38πe7m2∈30h5Bμ0Z28πe7m2∈30h5Cμ0πZ38e7m2∈30h5Dμ0πZ28e7m2∈30h5The key feature of Bohr'[s spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton we will extend this to a general rotational motion to find quntized rotantized rotational energy of a diatomic molecule assuming it to be right . The rate to energy applied is Bohr's quantization condition
it is found that the excitation from ground to the first excited state of rotation for the CO molecule is close to 4π×1011Hz then the moment of inertia of CO molecule about its center of mass is close to
(Takeh=2π×10−34Js)A2.76×10−46kgm2B1.87×10−46kgm2C4.67×10−47kgm2D1.17×10−47kgm2It is tempting to think that all possible transition are permissible and that an atomic spectrum arises from the transition of an electron from any initial orbital to any other orbital .However this is not so because a photon a photon has as intrinsic spin angular momentum of √2h/2π corresponding to S=1 although it has no charge and no rest mass
On the other hand , an electron has got two type of angular momentum: orbital angular momentum
L=[√l(l+1)]h/2π,and spin angular momentum L1=√s(s+1)h/2π arising from orbital motion and spin motion of the electron during any electronic transition must compensate for the angular momentum carried away by the photon .To satisfy this condition the different between the azimuthal quantum number of the orbital within which the transition take place must differ by 1.thus, an electron in a d-orbital (l=2) cannot make a transition into as s-orbital (l=0)because the photon cannot carry away enough angular momentum
The maximum orbital angular momentum of an electron with n=5 isA√2h2πB√6h2πC√12h2πD√20(h2π)
If Bohar 's quantisation postulate ( angular momentum = nh/2π) is a basic law of nature , it should be equal be equally valid for the case of planetary motion also . Why then do we never speak of quatisation of orbit of planets around the Sun ?
View SolutionWhile studying the theory of planetary motion, kepler established three laws. According to kepler's second law, the line joining a planet to the sun sweeps out equal areas in equal intervals of time, i.e., the areal velocity of the planet around the sun is constant. This led him to conlude from the sun.
Read the above passege and answer the following questions :
(i) What is the basis of kepler's second law?
(ii) Mercury is closer to the sun than the earth. Will time period of mercury be less or more than one year ? Why ?
(iii) What value of life do you learn from kepler's second law?
View SolutionL=√l(l+1)h2π
On the other hand, m determines Z-component of orbital angular momentum as Lz=m(h2π)
Hund's rule states that in degenerate orbitals electron s do not pair up unless and until each such orbital has got an electron with parallel spins. Besides orbital motion, an electron also possess spin-motion. spin may be clockwise and anti-clockwise. Both thes spin motions are called two spin states of electron characterised by spin. s=+12 and s=−12, respectively.
The orbital angular momentum of electron (l=1) makes an angle of 45∘ from Z-axis. The Lz of electron will be
View SolutionConsider the following statements regarging Bohr atomic model-
1. It introduces the ideal of stationary orbits.
2. It assumes the angular momentum of electron equal to −(12)h2π
3. It uses planetary model of the atom involving circular orbits
Which of the statements given above are correct?
View SolutionThe motion of a planet around sun in an elliptical orbit is shown in the following figure. Sun is situated at one focus. The shaded areas are equal. If the planet takes time t1 and l2 in moving from A to B and from C to D respectively, then
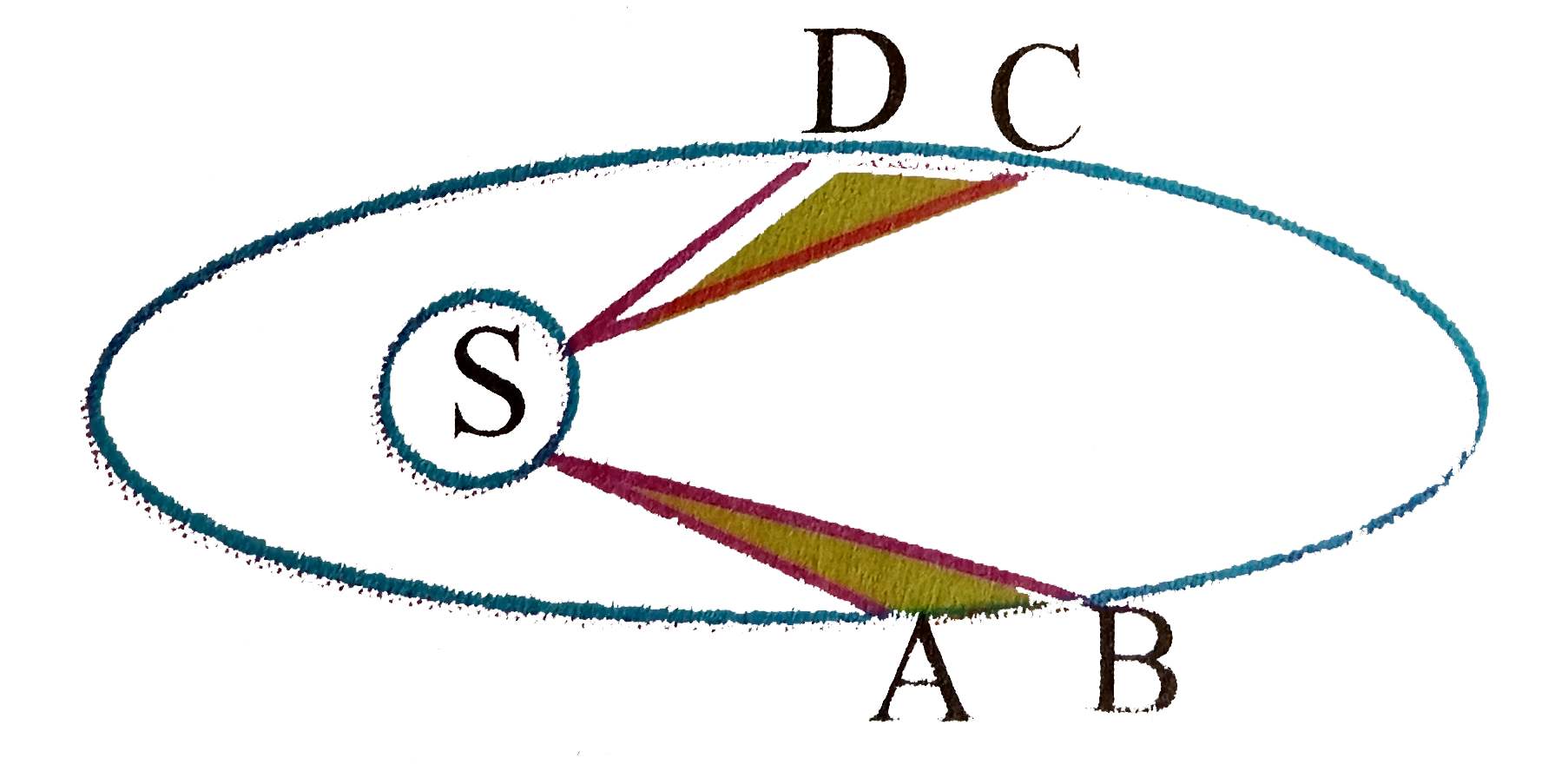
View Solution
