If current density →J is defined as a vecto with magniutde equal tpo current per unit area, area being normal to the current and direction in which current flows, show that I=∫→J.d→s
By definition
→J=dIdscosθˆk
or ˆkdI=→Jdscosθt
or ˆkdI=Jdscostheatˆk [asˆJ=Jˆk]
Now , taking scalar product of both sides with ˆk,
ˆk.ˆkdI=Jdscosθˆk.ˆk
or dI=Jdscosθ " "[as ˆk.ˆk=1] ....(i)
But by denfinition of scalar product of two vectors,
→J.d→s=Jdscosθ ......(ii)
So, from Eqns. (i) and (ii), we have
dI=→J.d→sorI=∫→J.d→s
Similar Questions
At a small distance from a solenoid carrying a current thero is placed a contour with a current in such a manner that the solenoid's axis lies in the plane of the contour. The directions of the currents in solenoid and contour are shown by arrows. How docs the contour move? I-Iow will it IJlOVe if the current in it flows in the direction opposite to the one shown in the figure?
View SolutionFour parallel conductors, carrying equal currents, pass vertically through the four corners of a square WXYZ. In two conductors, the current is flowing into the page, and in the other two out into the page, and in the other two out of the page. In what directions must the currents flow to produce a resultant magnetic field in the direction shown at O, the centre of the square?

View Solution
Knowledge Check
A:Current density is a very is a vector quantity .
R : Electric current , passing through a given unit area is current density.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion , then markBIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion then mark.CIf Assertion is ture statement but Reason is false , then markDIf both Assertion and Reason are false statements then mark.If →j and →E are current and electric field inside a current carrying conductor at an instant then →j.Vec(E) is
(1) Positive (2) Negative
(3) Zero (4) May be positive or negativeAPositiveBNegativeCZeroDMay be positive or negativeIn the circuit diagram show below, the magnitude and direction of the flow of current respectively would be -
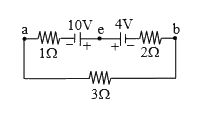 A7/3 amp. from a to b via eB7/3 amp. from b to a via eC1.0 amp. from b to a via eD1.0 amp. from a to b via e
A7/3 amp. from a to b via eB7/3 amp. from b to a via eC1.0 amp. from b to a via eD1.0 amp. from a to b via e
When current flows through copper wire, current density J, electric field E and motion of electrons have directions such that
View SolutionA : For a given conductor , electric current does not vary even if its cross sectional area varies .
R : A conductor remains unchanged when current flows through it .
View SolutionIn the electrical method of magnetization, the polarity of the end in which current flows in clockwise direction
View SolutionIn the electrical method of magnetization, the polarity of the end in which current flows in clockwise direction
View Solutionवृत्त के आकार में एक धारावाही तार (धारा I के साथ) पर विचार करें। ध्यान रहे कि जैसे-जैसे धारा तार में आगे बढ़ती जाती है वैसे-वैसे →J (धारा घनत्व) की दिशा एक समग्र रूप से परिवर्तित होती है, जबकि धारा । अप्रभावित रहती है। इसके लिए आवश्यक रूप से उत्तरदायी है
View Solution
