If E,M,J,andG , respectively , denote energy , mass , angular momentum , and gravitational constant , then EJ2/M5G2 has the dimensions of
mass
length
time
angle
The correct Answer is:D
To find the dimensions of the expression EJ2M5G2, we will break down the dimensions of each variable involved: energy (E), angular momentum (J), mass (M), and gravitational constant (G).
Step 1: Determine the dimensions of each variable.
1. Energy (E):
- The dimension of energy is given by:
(E)=M1L2T−2
2. Angular Momentum (J):
- The dimension of angular momentum is given by:
(J)=M1L2T−1
3. Mass (M):
- The dimension of mass is:
(M)=M1
4. Gravitational Constant (G):
- The dimension of the gravitational constant is:
(G)=M−1L3T−2
Step 2: Substitute the dimensions into the expression.
Now we substitute these dimensions into the expression EJ2M5G2.
- Substitute for E:
E=M1L2T−2
- Substitute for J2:
J2=(M1L2T−1)2=M2L4T−2
- Substitute for M5:
M5=(M1)5=M5
- Substitute for G2:
G2=(M−1L3T−2)2=M−2L6T−4
Step 3: Combine the dimensions.
Now we can combine these dimensions in the expression:
EJ2M5G2=(M1L2T−2)(M2L4T−2)M5(M−2L6T−4)
Step 4: Simplify the expression.
Let's simplify the numerator and the denominator separately.
- Numerator:
EJ2=M1L2T−2⋅M2L4T−2=M1+2L2+4T−2−2=M3L6T−4
- Denominator:
M5G2=M5⋅M−2L6T−4=M5−2L6T−4=M3L6T−4
Now, substituting back into the expression:
M3L6T−4M3L6T−4=M3−3L6−6T−4+4=M0L0T0
Step 5: Conclusion.
Since M0L0T0 indicates that the expression is dimensionless, we can conclude that:
The dimensions of EJ2M5G2 is M0L0T0
This corresponds to the dimensions of an angle, which is also dimensionless.
Final Answer:
The dimensions of EJ2M5G2 is M0L0T0 (dimensionless).
---
1. Energy (E):
- The dimension of energy is given by:
(E)=M1L2T−2
- The dimension of angular momentum is given by:
(J)=M1L2T−1
- The dimension of mass is:
(M)=M1
- The dimension of the gravitational constant is:
(G)=M−1L3T−2
Now we substitute these dimensions into the expression EJ2M5G2.
E=M1L2T−2
J2=(M1L2T−1)2=M2L4T−2
M5=(M1)5=M5
G2=(M−1L3T−2)2=M−2L6T−4
Now we can combine these dimensions in the expression:
EJ2M5G2=(M1L2T−2)(M2L4T−2)M5(M−2L6T−4)
Let's simplify the numerator and the denominator separately.
EJ2=M1L2T−2⋅M2L4T−2=M1+2L2+4T−2−2=M3L6T−4
M5G2=M5⋅M−2L6T−4=M5−2L6T−4=M3L6T−4
M3L6T−4M3L6T−4=M3−3L6−6T−4+4=M0L0T0
Since M0L0T0 indicates that the expression is dimensionless, we can conclude that:
The dimensions of EJ2M5G2 is M0L0T0
This corresponds to the dimensions of an angle, which is also dimensionless.
The dimensions of EJ2M5G2 is M0L0T0 (dimensionless).
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Higher Order Thinking Skills
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Exemplar Problems
12 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion And Reason
15 Videos
- WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
If E, M, L and G denote energy, mass, angular momentum and gravitational constant repectively then the quantity (E2L2/M5G2) has the dimensions of :-
View SolutionIn the expression P=EL2m−5G−2, E, m, L and G denote energy, mass, angular momentum and gravitational constant, respectively. Show that P is a dimensionless quantity.
View SolutionIf J is the angular momentum and E is the kinetic energy, then J2E has the dimensions of
View Solutionh d G has the dimensions of (h = height , d = density , G = Gravitational constant)
View SolutionIf E = energy , G= gravitational constant, I=impulse and M=mass, then dimensions of GIM2E2 are same as that of
View SolutionThe escape velocity of a sphere of mass m is given by (G= univesal gravitational constant, Me= mass of the earth and Re= radius of the earth)
View SolutionKepler's third law states that square of period revolution (T) of a planet around the sun is proportional to third power of average distance i between sun and planet i.e. T2=Kr3
here K is constant
if the mass of sun and planet are M and m respectively then as per Newton's law of gravitational the force of alteaction between them is F=GMmr2, here G is gravitational constant. The relation between G and K is described as
View SolutionA planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are R1 and R2 respectively. Ignore the gravitational force between the satellites. Define v1,L1,K1 and T1 to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and v2,L2,K2 and T2 to be he corresponding quantities of satellite 2. Given m1/m2=2 and R1/R2=1/4, match the ratios in List-I to the numbers in List-II.
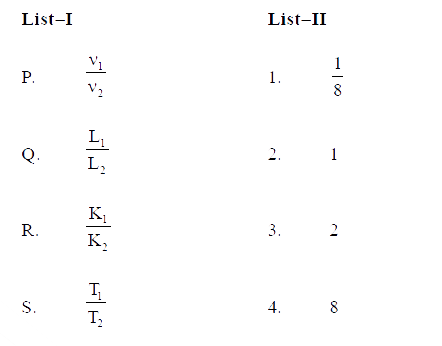
View SolutionThe acceleration due to gravity at a piece depends on the mass of the earth M, radius of the earth R and the gravitational constant G. Derive an expression for g?
View SolutionThe relation between angular momentum J of a body and rotational kinetic energy is given by J=√2EI. The graph between J and √E will be:
View Solution