Question

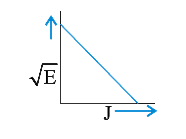
The relation between angular momentum J of a body and rotational kinetic energy is given by $J=\sqrt{2EI}$. The graph between J and $\sqrt{E}$ will be:

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem, we need to analyze the relationship between angular momentum $$J$$ and rotational kinetic energy $$E$$ as given by the equation:

$$J=\sqrt{2EI}$$

1. Identify the Variables:
- We have \( J \) as the angular momentum.
- We have \( E \) as the rotational kinetic energy.
- We need to establish the relationship between \( J \) and \( \sqrt{E} \).

2. Rearranging the Equation:
- From the equation \( J = \sqrt{2EI} \), we can express \( J \) in terms of \( \sqrt{E} \):
\( J = \sqrt{2I} \cdot \sqrt{E} \)
- This shows that \( J \) is directly proportional to \( \sqrt{E} \).

3. Understanding the Proportionality:
- Since \( J \) is directly proportional to \( \sqrt{E} \), we can write:
\( J = k \cdot \sqrt{E} \)
where \( k = \sqrt{2I} \) is a constant.

4. Graphical Representation:
- In a graph where \( J \) is plotted on the Y-axis and \( \sqrt{E} \) is plotted on the X-axis, the relationship \( J = k \cdot \sqrt{E} \) indicates that the graph will be a straight line.
- The slope of the line is positive since \( k \) is a positive constant.

5. Intercept Analysis:
- If \( \sqrt{E} = 0 \), then \( J \) will also be \( 0 \). This means the graph passes through the origin (0,0).

6. Conclusion:
- Therefore, the graph between \( J \) and \( \sqrt{E} \) is a straight line that passes through the origin and has a positive slope.

Final Answer:
The graph between \( J \) and \( \sqrt{E} \) will be a straight line passing through the origin.

---