If denotes the value of acceleration due to gravity at a point distance from the centre of earth of radius . If , then
The correct Answer is:B
To solve the problem, we need to determine how the acceleration due to gravity g varies with the distance r from the center of the Earth when r<R (where R is the radius of the Earth).
1. Understanding the Gravitational Force:
The gravitational force F acting on a mass m at a distance r from the center of the Earth is given by Newton's law of gravitation:
F=GMmr2
where G is the gravitational constant and M is the mass of the Earth.
2. Relating Force to Acceleration:
The acceleration due to gravity g at distance r can be expressed as:
g=Fm=GMr2
Here, g is the acceleration due to gravity at distance r.
3. Considering the Case When r<R:
When r is less than R, we need to consider only the mass of the Earth that is enclosed within the radius r. According to the shell theorem, the gravitational attraction inside a uniform spherical shell of mass is zero. Thus, only the mass of the Earth within radius r contributes to the gravitational force.
4. Finding the Mass Enclosed:
The mass menclosed within radius r can be calculated using the density ρ of the Earth:
menclosed=ρ⋅43πr3
The density ρ can be expressed in terms of the total mass M of the Earth and its volume:
ρ=M43πR3
5. Substituting Back into the Gravitational Formula:
Now, substituting menclosed into the gravitational force equation:
g=Gmenclosedr2=G(ρ⋅43πr3)r2
Simplifying this gives:
g=G⋅M43πR3⋅43πr3r2=GMR3r
6. Conclusion:
From the derived equation, we can see that:
g∝r
This means that the acceleration due to gravity g is directly proportional to the distance r from the center of the Earth when r<R.
Final Answer:
The relationship is g∝r for r<R.
The gravitational force F acting on a mass m at a distance r from the center of the Earth is given by Newton's law of gravitation:
F=GMmr2
where G is the gravitational constant and M is the mass of the Earth.
The acceleration due to gravity g at distance r can be expressed as:
g=Fm=GMr2
Here, g is the acceleration due to gravity at distance r.
When r is less than R, we need to consider only the mass of the Earth that is enclosed within the radius r. According to the shell theorem, the gravitational attraction inside a uniform spherical shell of mass is zero. Thus, only the mass of the Earth within radius r contributes to the gravitational force.
The mass menclosed within radius r can be calculated using the density ρ of the Earth:
menclosed=ρ⋅43πr3
The density ρ can be expressed in terms of the total mass M of the Earth and its volume:
ρ=M43πR3
Now, substituting menclosed into the gravitational force equation:
g=Gmenclosedr2=G(ρ⋅43πr3)r2
Simplifying this gives:
g=G⋅M43πR3⋅43πr3r2=GMR3r
From the derived equation, we can see that:
g∝r
This means that the acceleration due to gravity g is directly proportional to the distance r from the center of the Earth when r<R.
The relationship is g∝r for r<R.
Topper's Solved these Questions
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - FILL IN THE BLANKS
11 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - PROBLEMS FOR PRACTIVE A
1 Videos
- GRAVIATIONBOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - CURIOSITY QUESTION
1 Videos
- BEHAVIOUR OF PERFECT GAS & KINETIC THEORYBOOK - PRADEEPCHAPTER - BEHAVIOUR OF PERFECT GAS & KINETIC THEORYEXERCISE - Assertion - Reason Type questions
14 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
Similar Questions
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be sphere of radius R of uniform density is a shown in figures along side.
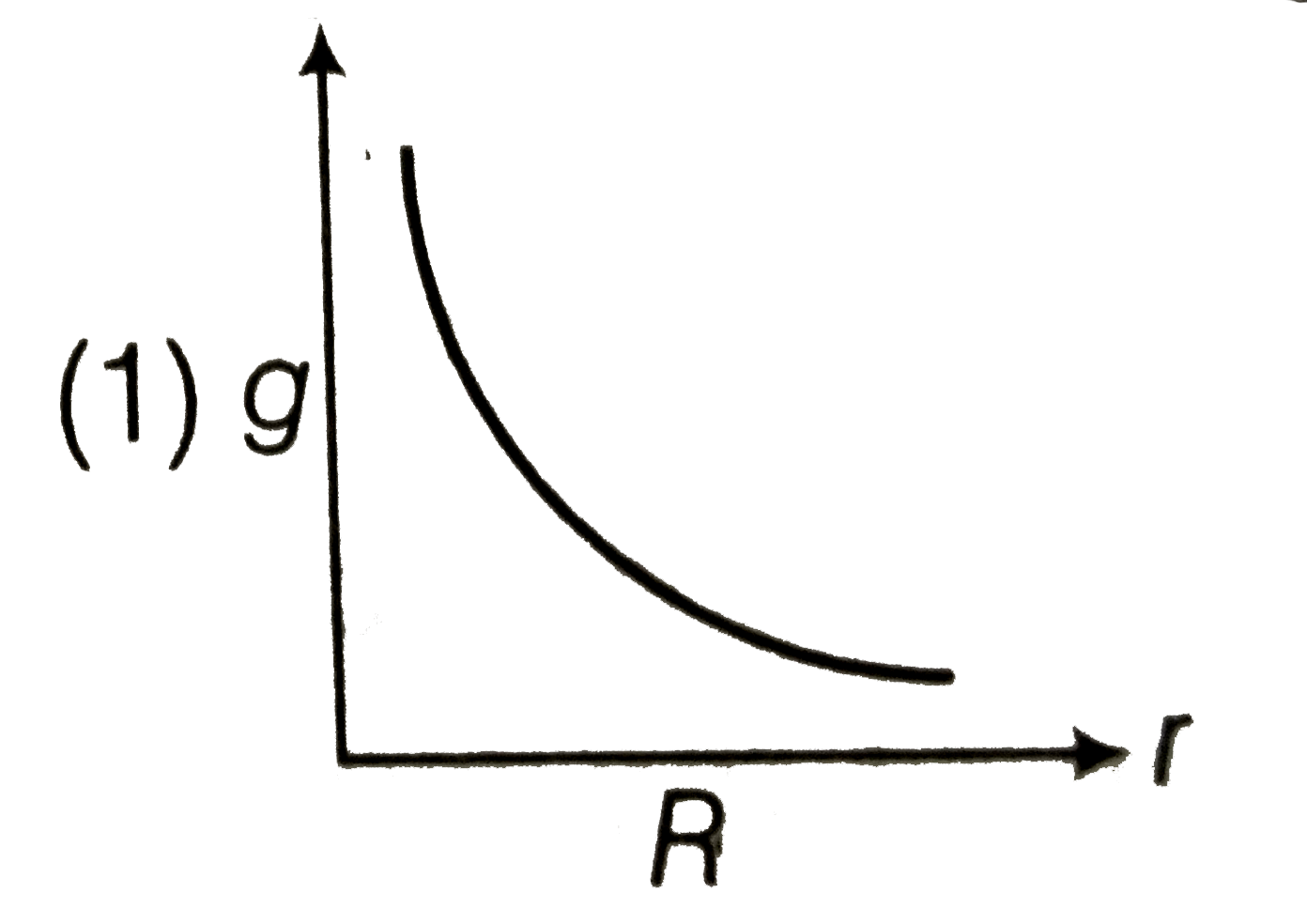
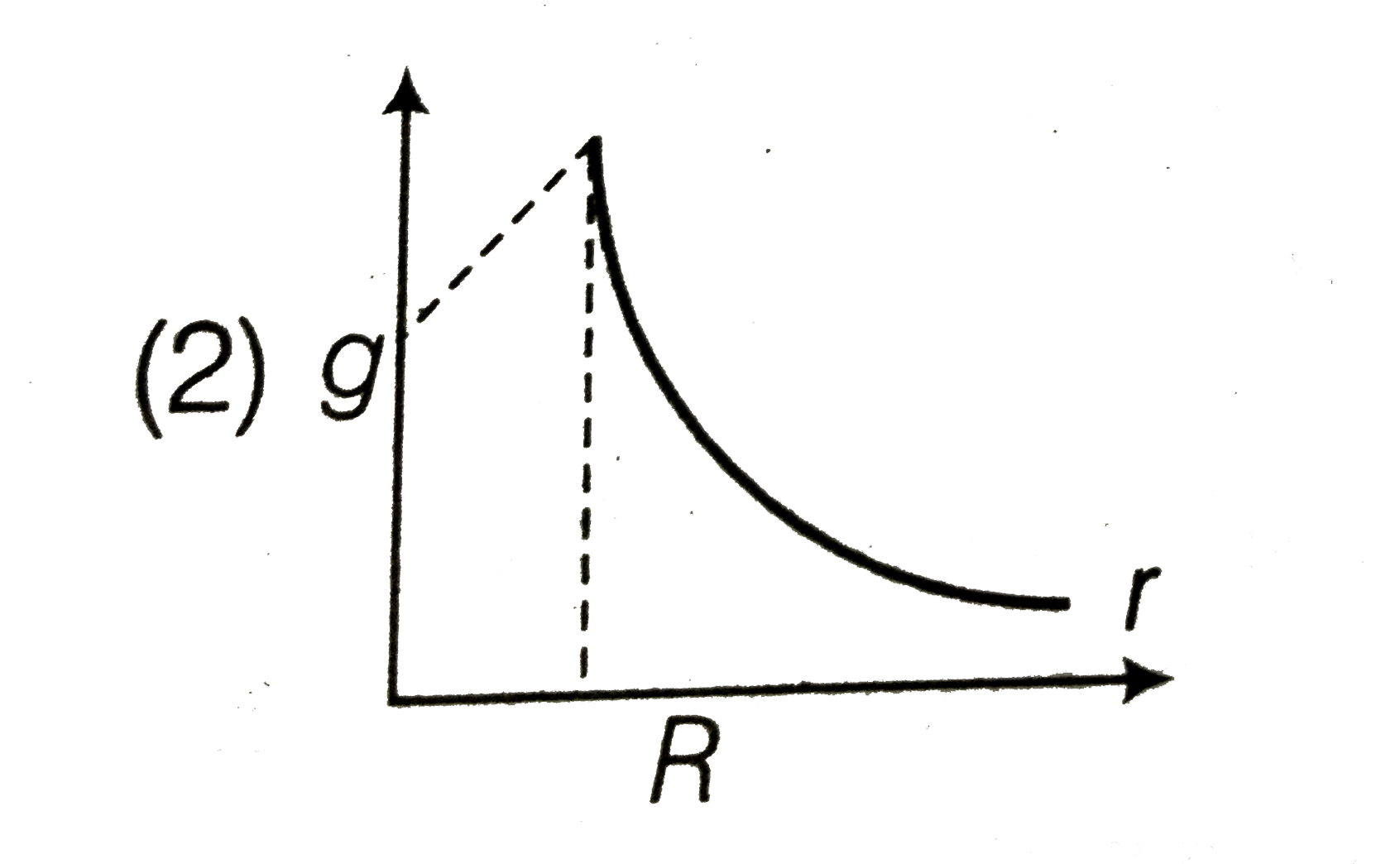
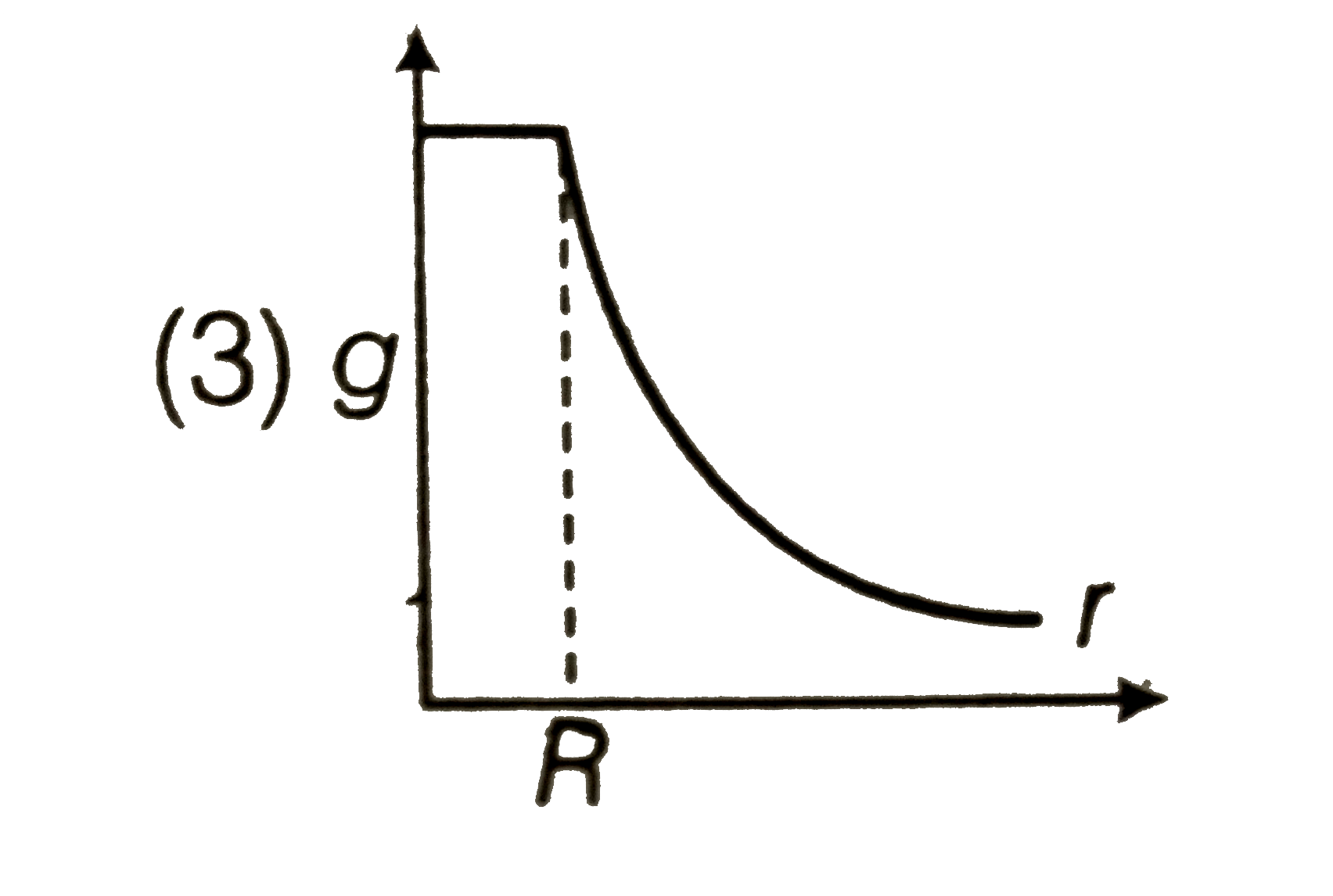
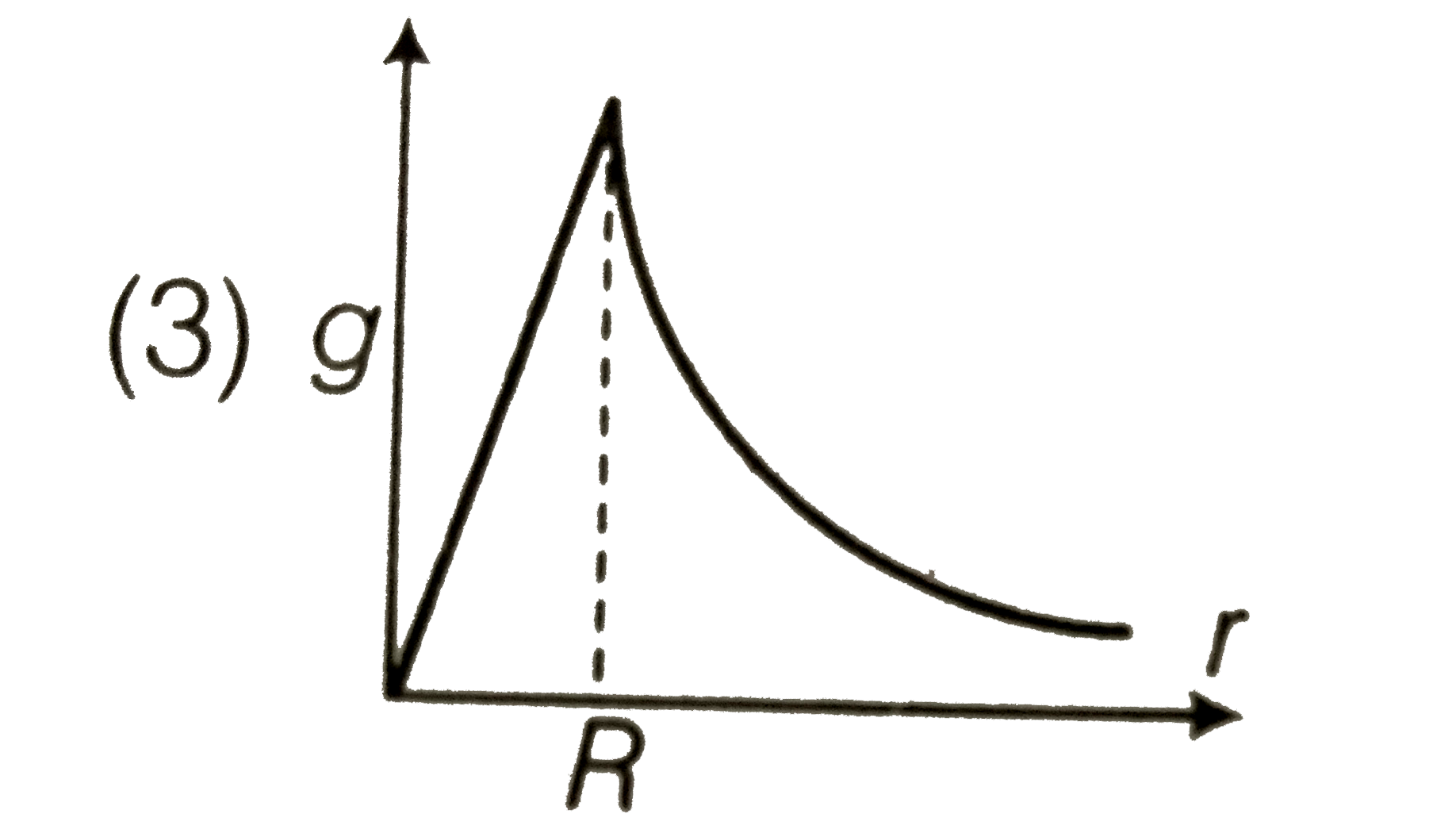
The correct figure is
View SolutionIf R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r<R) from the centre of the earth is proportional to
View Solution
Knowledge Check
The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
Ag∝rBg∝r2Cg∝r−1Dg∝r−2The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to br a sphere of radius R of uniform density is as shoen in Fig. below:
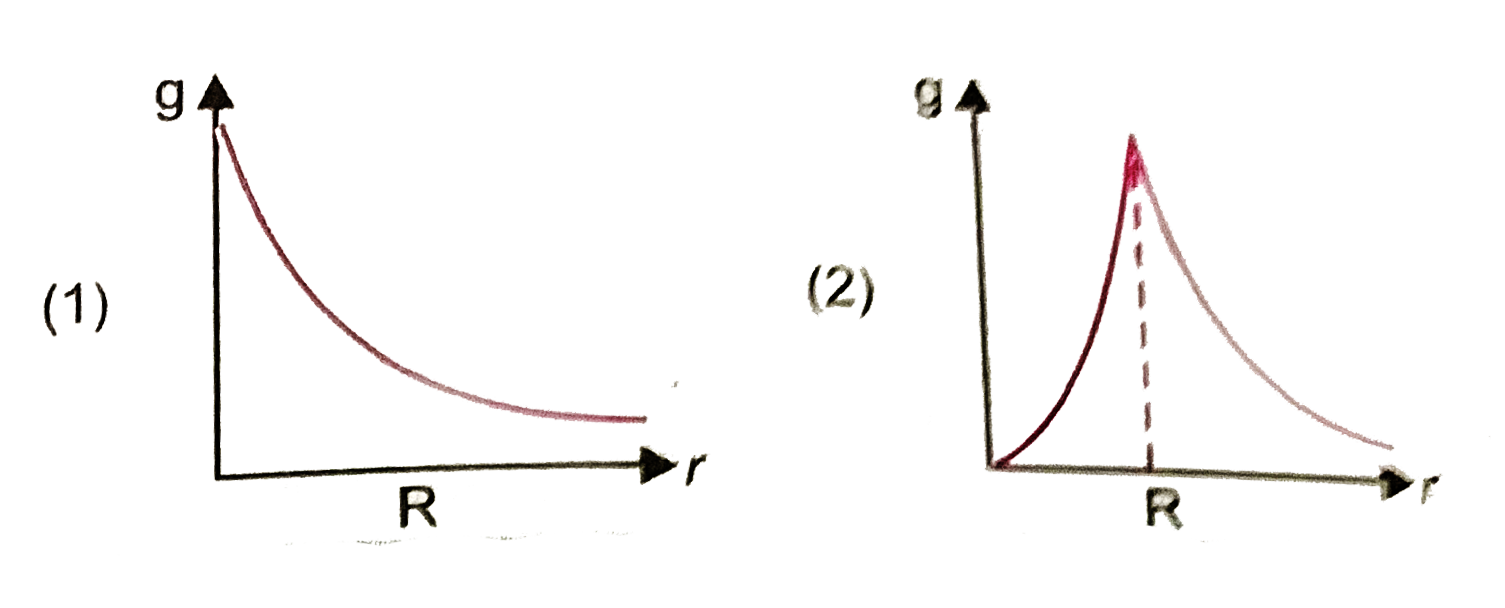
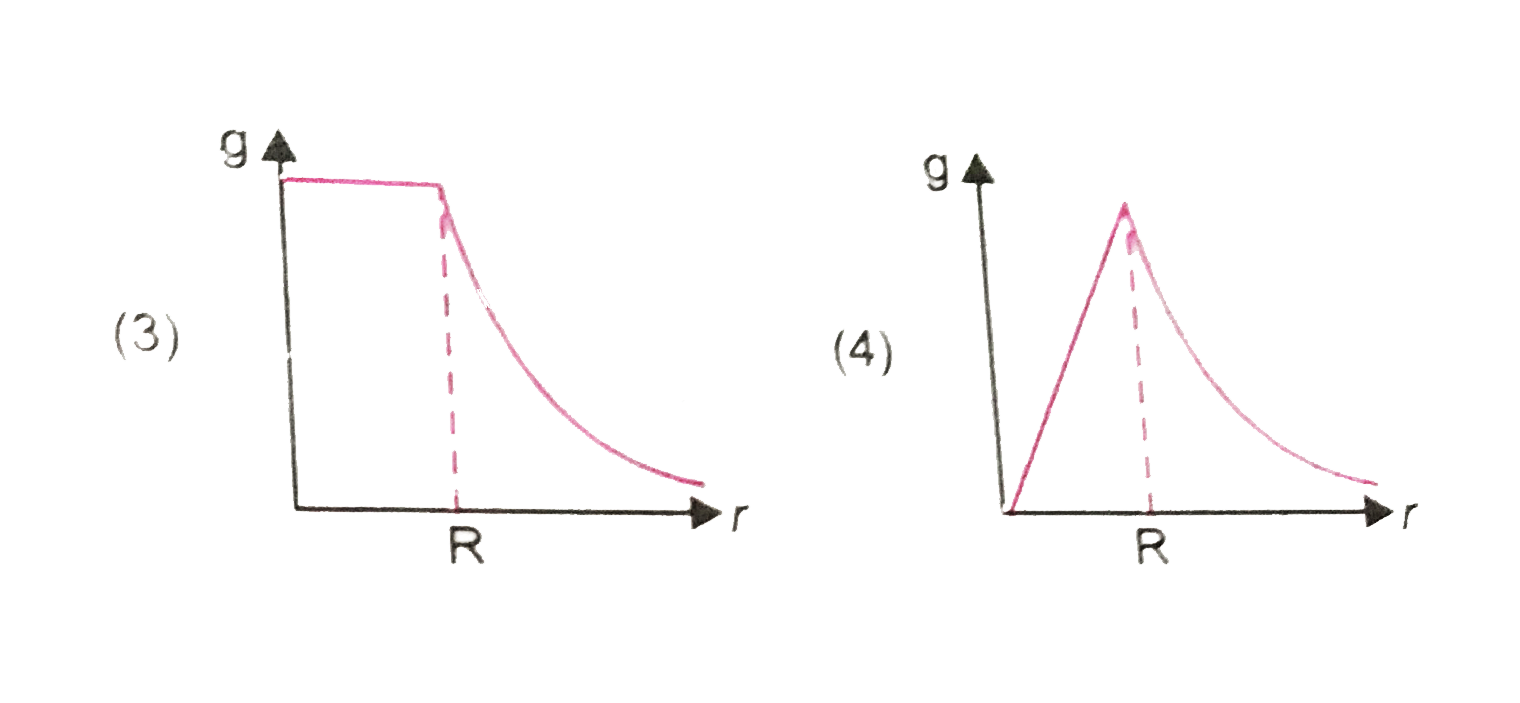
The correct figure isA(4)B(1)C(2)D(3)The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
A1/rB1/r2CrDr2
If R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r>R) from the centre of the earth is proportional to
View SolutionIf R is the radius of the earth, then the value of acceleration due to gravity at a height h from the surface of the earth will become half its value on the surface of the earth if
View SolutionVariation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R→ Radius of the Earth)
View SolutionThe depth at which the effective value of acceleration due to gravity is g4 is (R=radius of the earth)
View SolutionAt what distance from the centre of the earth, the value of acceleration due to gravity g will be half that on the surface ( R = radius of earth)
View Solution
