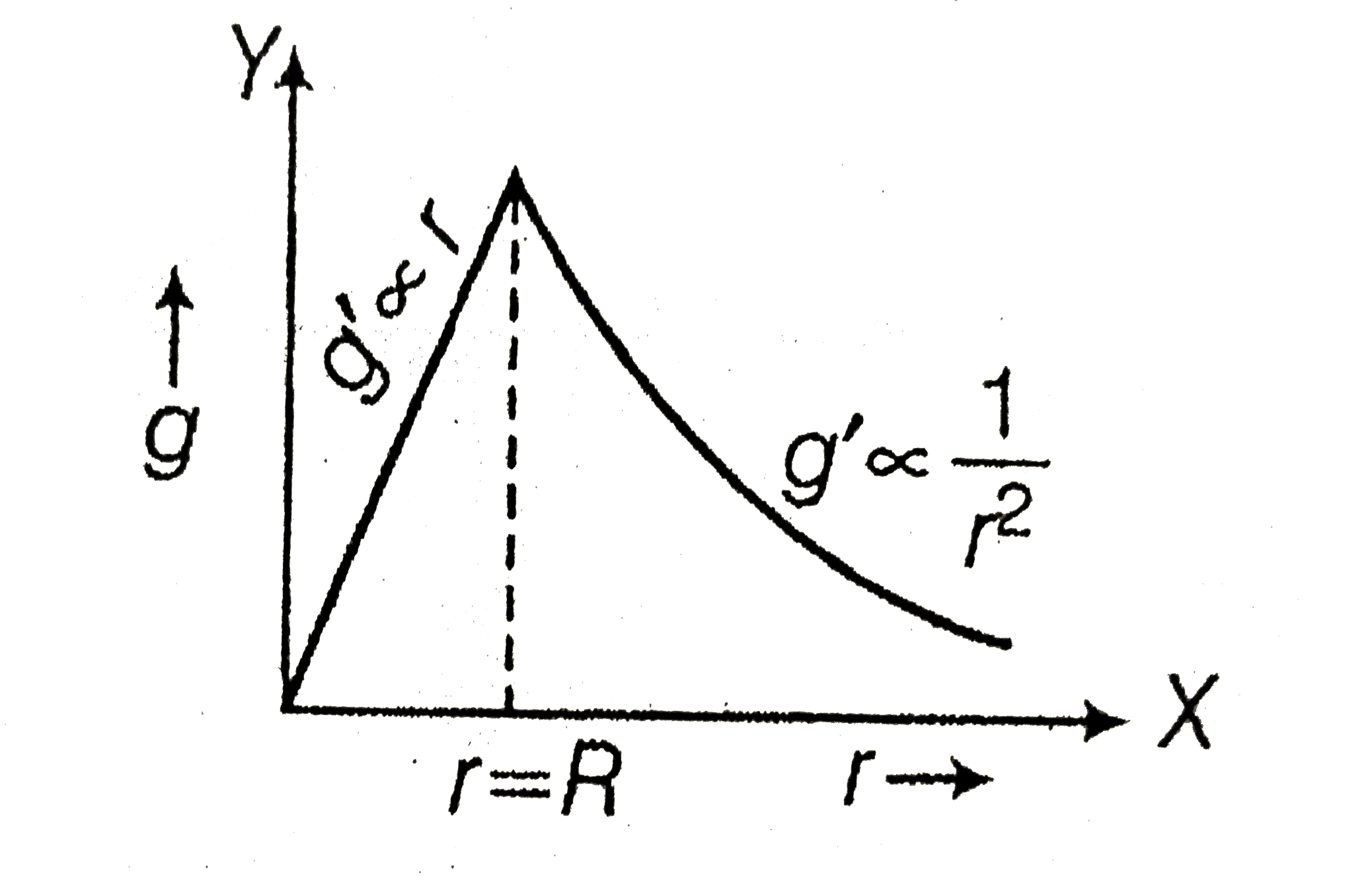
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to be sphere of radius R of uniform density is a shown in figures along side.
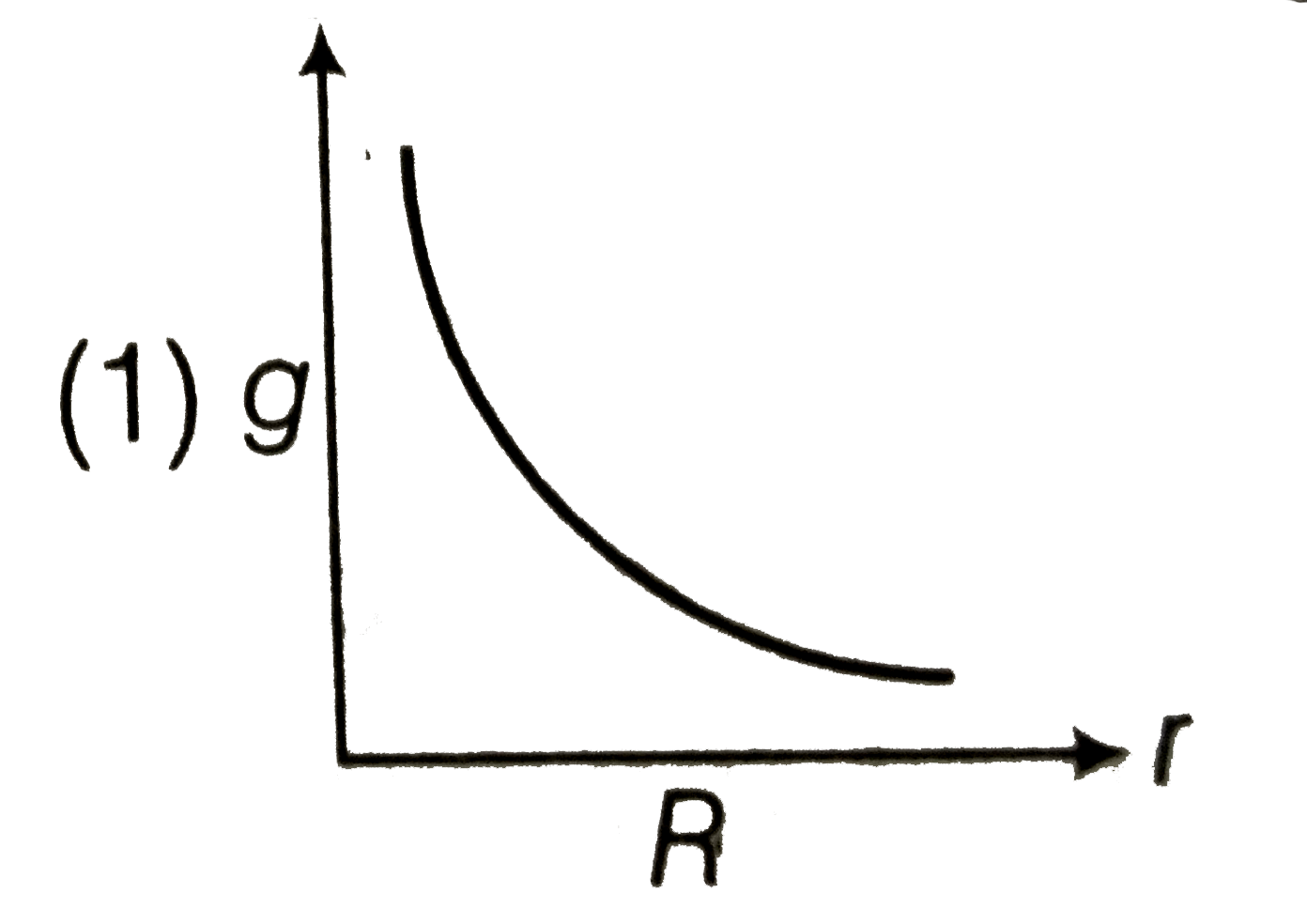
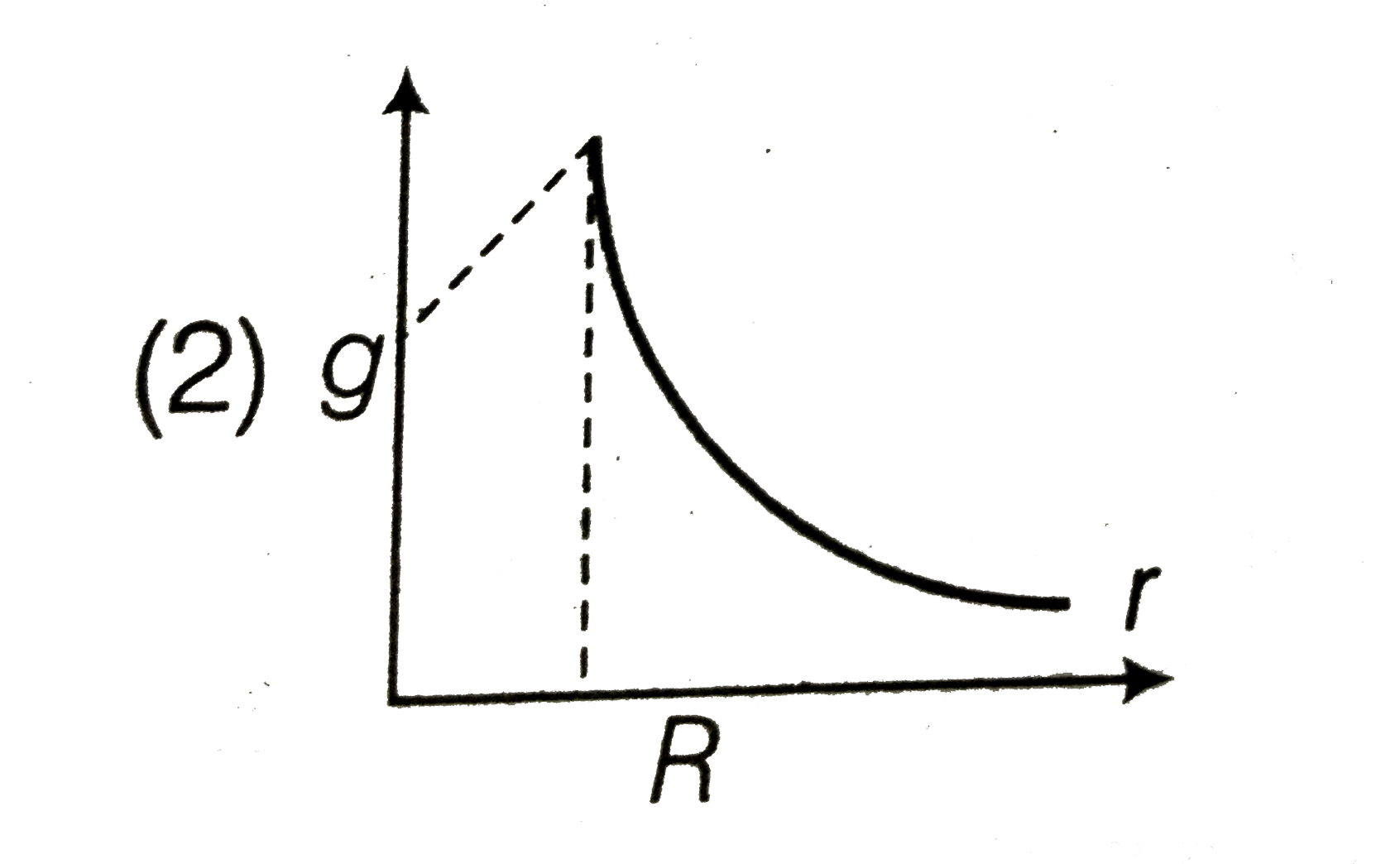
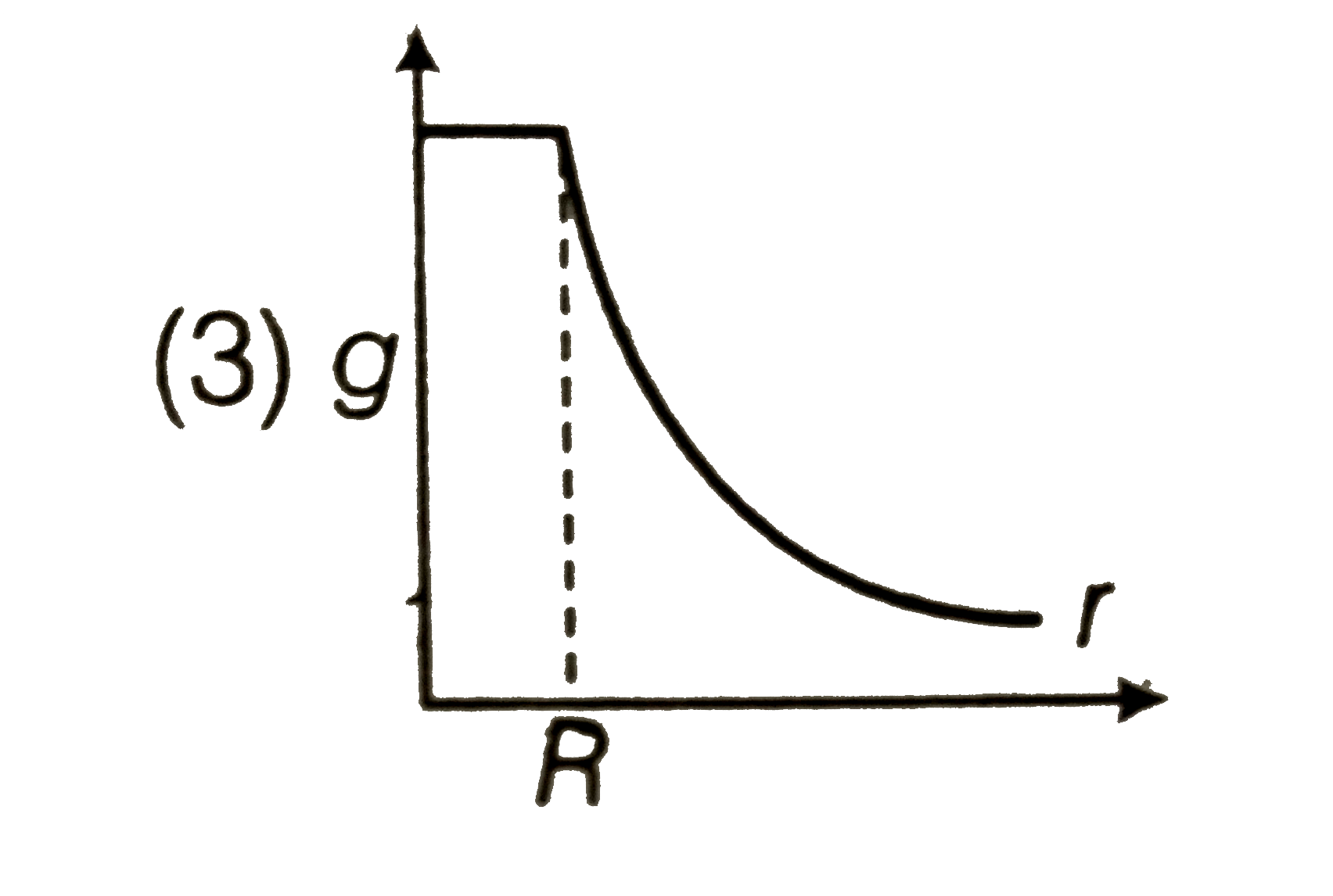
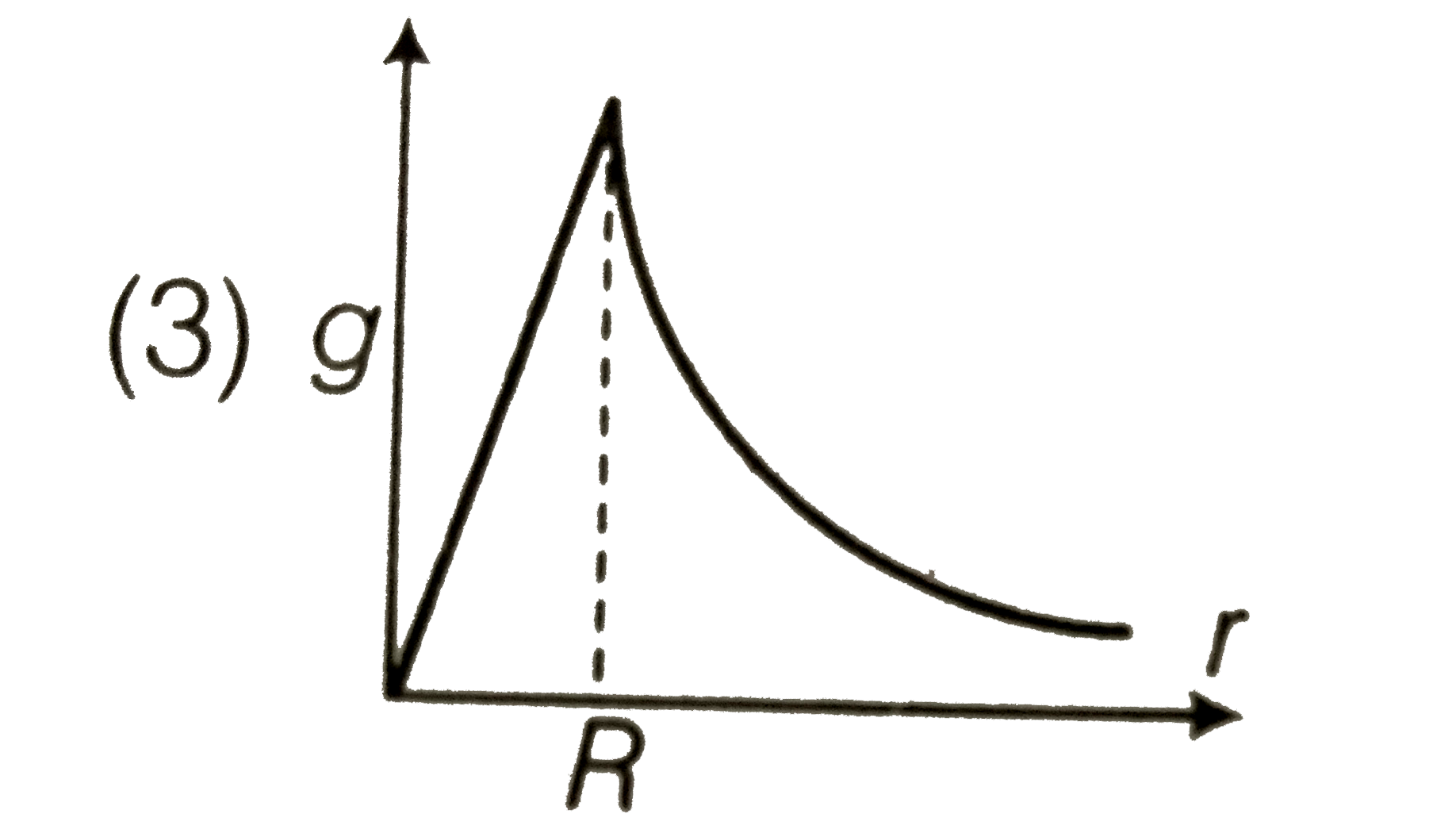
The correct figure is
A
-4
B
-1
C
-2
D
−3
Video Solution
Text Solution
The correct Answer is:A
The acceleration due to gravity at the depth d below surface of earth is given by
g'=GMR2(1−dR)=g(1−dR)
g'=0 at d=R
[valud of g at centre of earth is equal to zero]
Thus, the variation in value of g with r is
For r>R
g'=g(1+hR)2=gR2r2⇒g'∝1r2
Here R+h=r
for r<R,g'=g(1−dR)=grR
Here R−d=r⇒g'∝r
Therefore, the variation of g with distance from centre of the earth will be as shown in the graph.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The dependence of acceleration due to gravity g on the distance r from the centre of the earth, assumed to br a sphere of radius R of uniform density is as shoen in Fig. below:
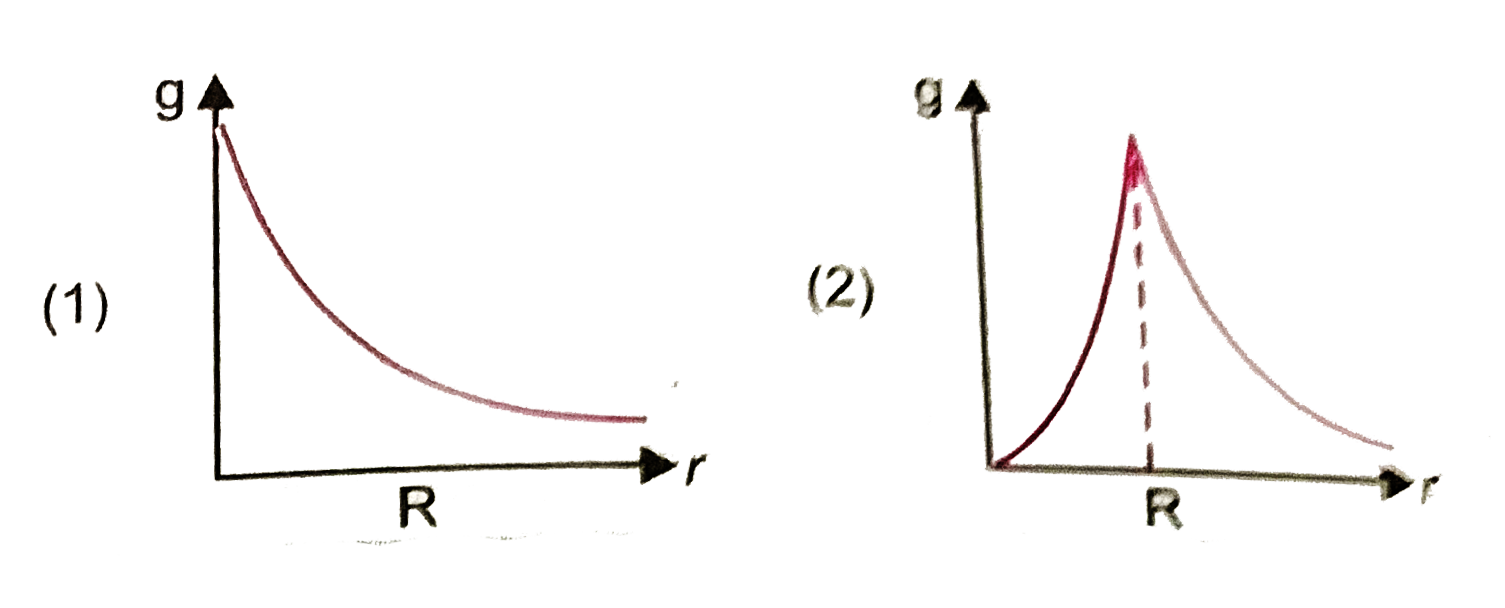
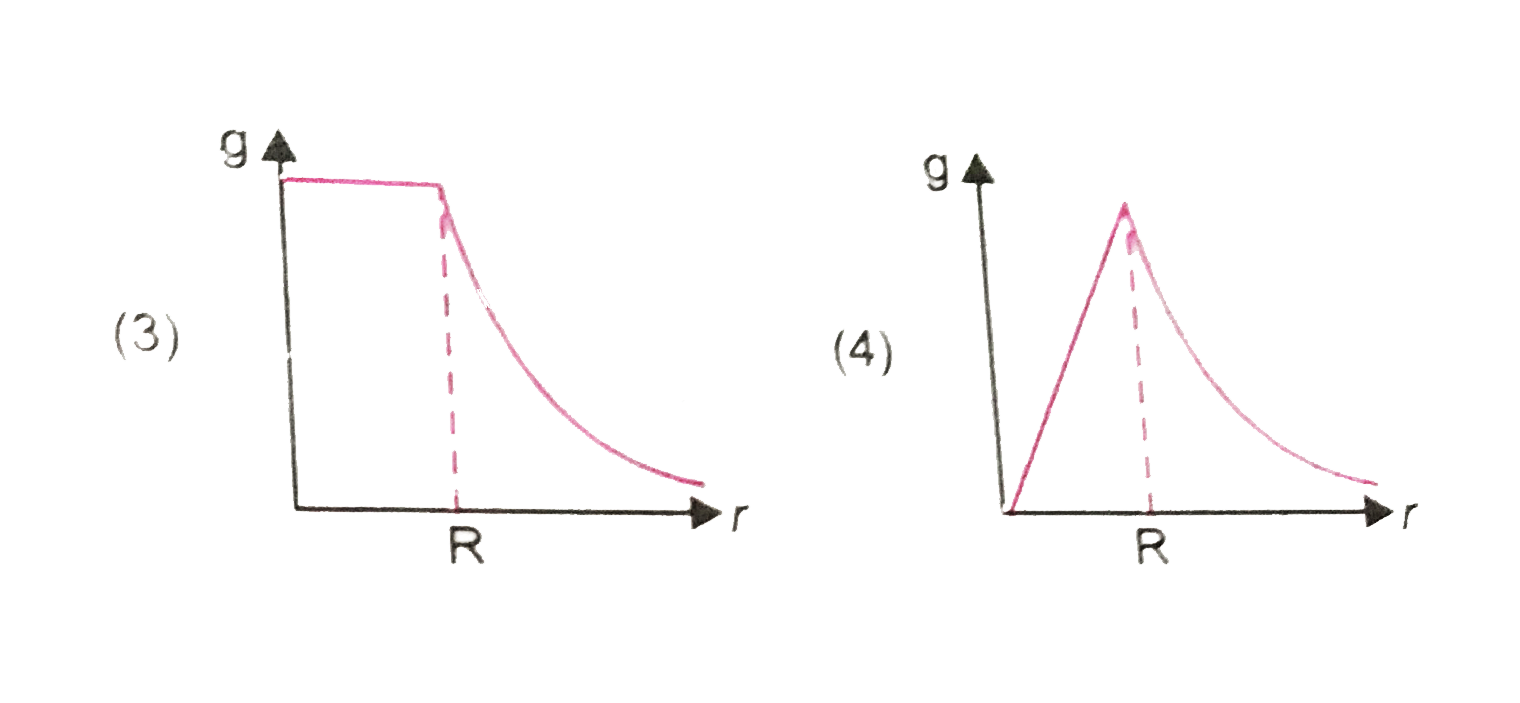
The correct figure isA(4)B(1)C(2)D(3) - Question 2 - Select One
Variation of acceleration due to gravity (g) with distance x from the centre of the Earth is best represented by (R→ Radius of the Earth)
A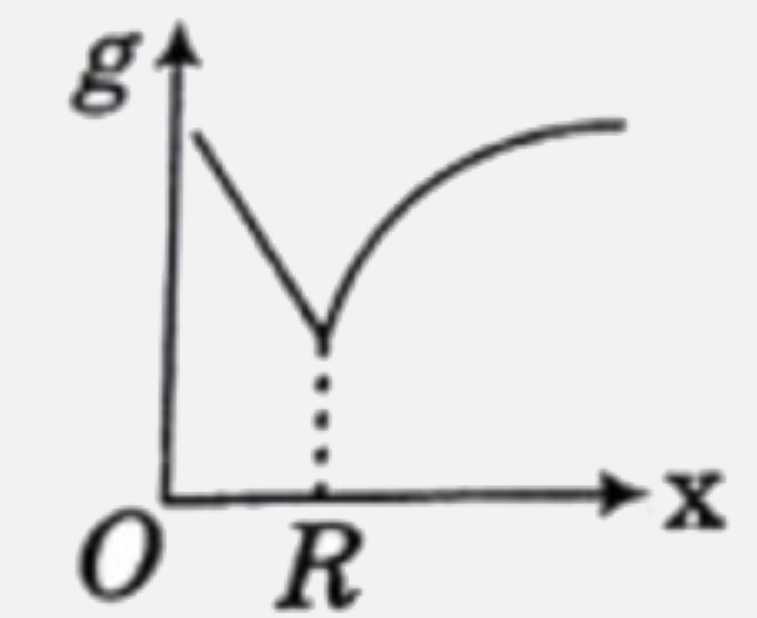 B
B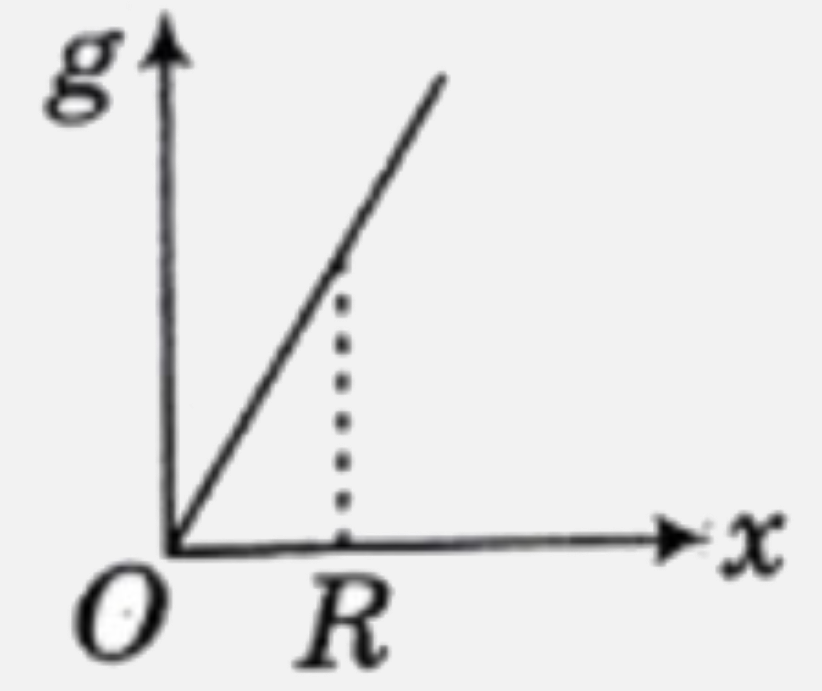 C
C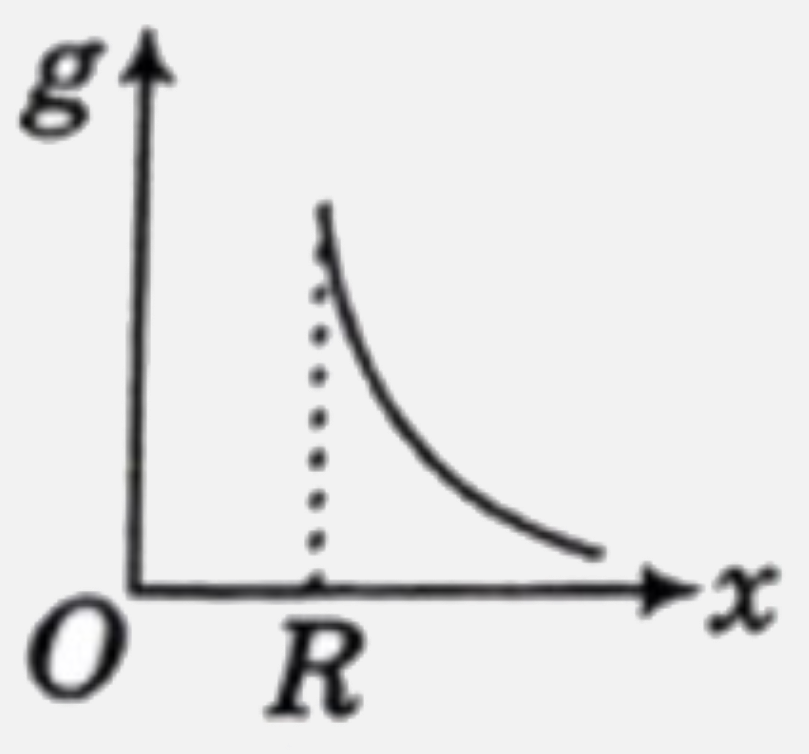 D
D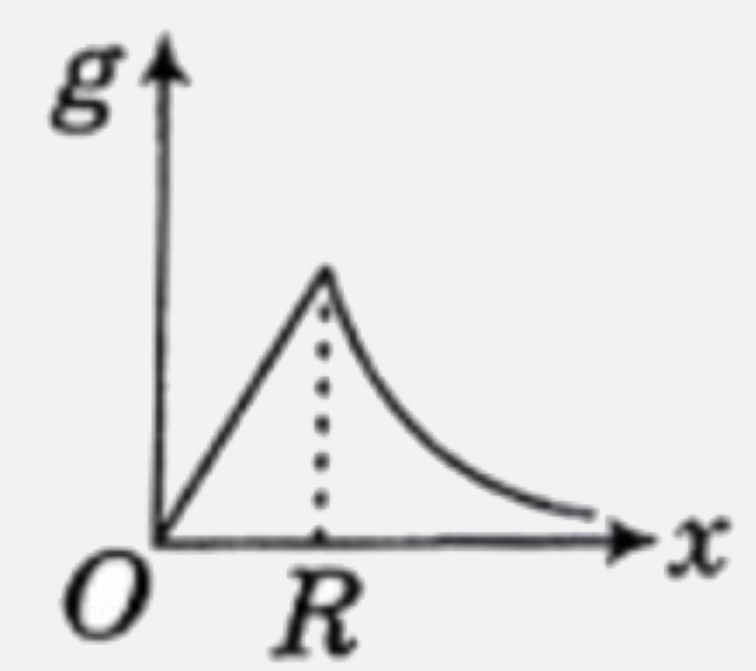
- Question 3 - Select One
The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
Ag∝rBg∝r2Cg∝r−1Dg∝r−2
The acceleration due to gravity is g at a point distant r from the centre of earth of radius R. If r<R, then
View SolutionIf g denotes the value of acceleration due to gravity at a point distance r from the centre of earth of radius R. If r<R, then
View SolutionThe value of g (acceleration due to gravity) at earth's surface is 10ms−2. Its value in ms−2 at the centre of the earth which is assumed to be a sphere of radius R metre and uniform mass density is
View SolutionFigure shows variation of acceleration due to gravity with distance from centre of a uniform spherical planet, Radius of planet is R. What is r1−r1
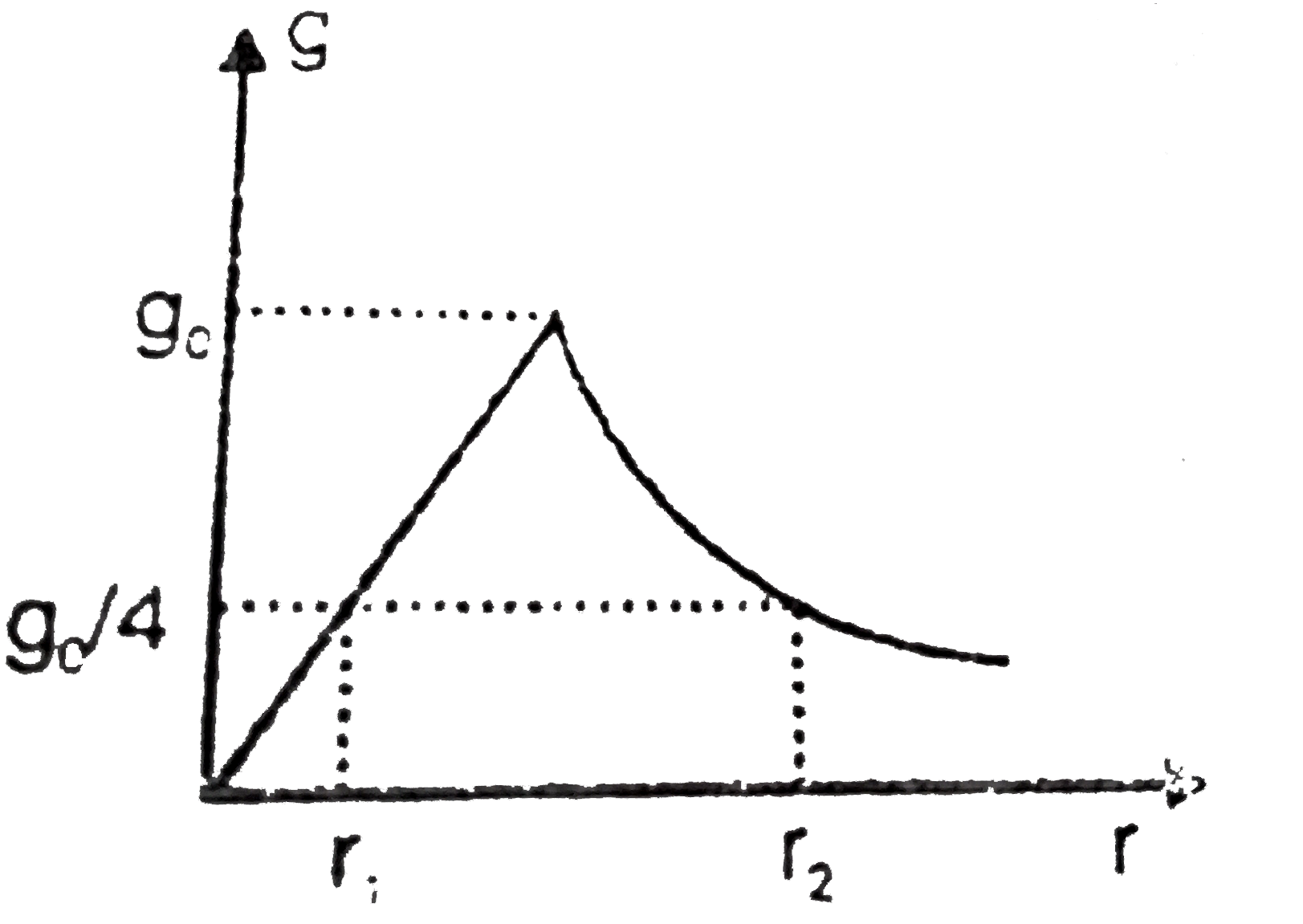 View Solution
View SolutionAssume the earth to be a sphere of uniform density the accleration due to gravity
View Solution

