If g is acceleration due to gravity on the surface of the earth, having radius R, the height at which the acceleration due to gravity reduces to g/2 is
R/2
√2R
R/√2
(√2−1)R
The correct Answer is:d
g2g1=(RR+h)2
g2g=(RR+h)2
1√2=RR+h
∴ R+h=√2R
h=√2R−R=R(√2−1).
Topper's Solved these Questions
Similar Questions
Knowledge Check
If g is the acceleration due to gravity on the surface of the earth , its value at a height equal to double the radius of the earth is
AgBg2Cg3Dg9Starting from the centre of the earth having radius R, the variation of g (acceleration due to gravity) is shown by
A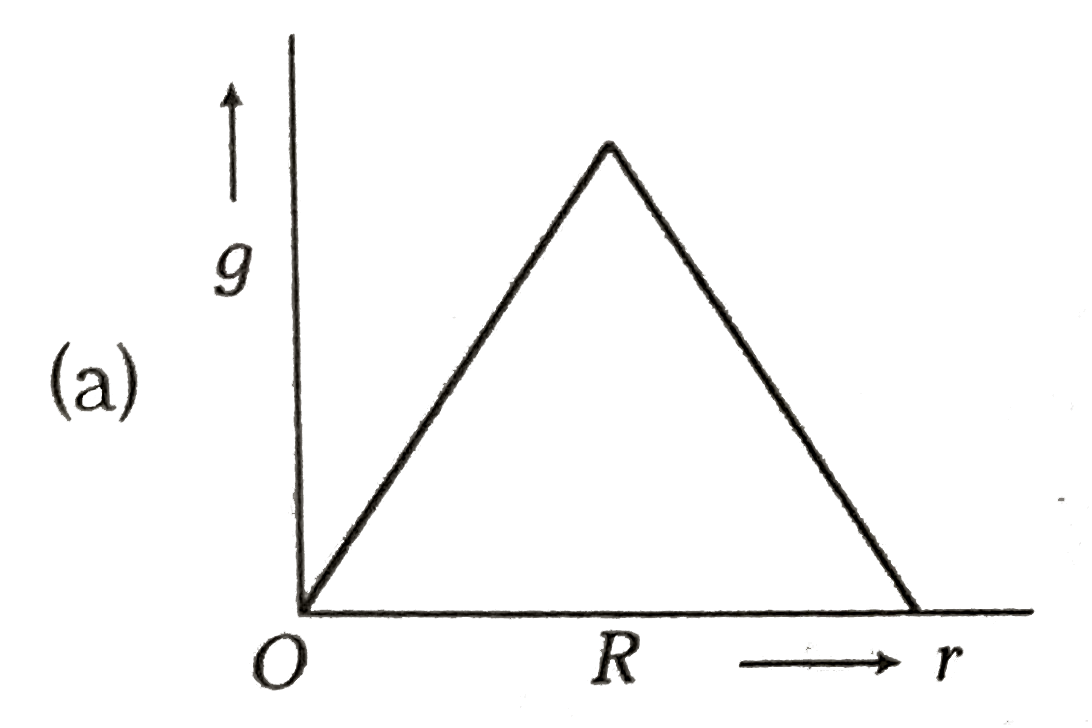 B
B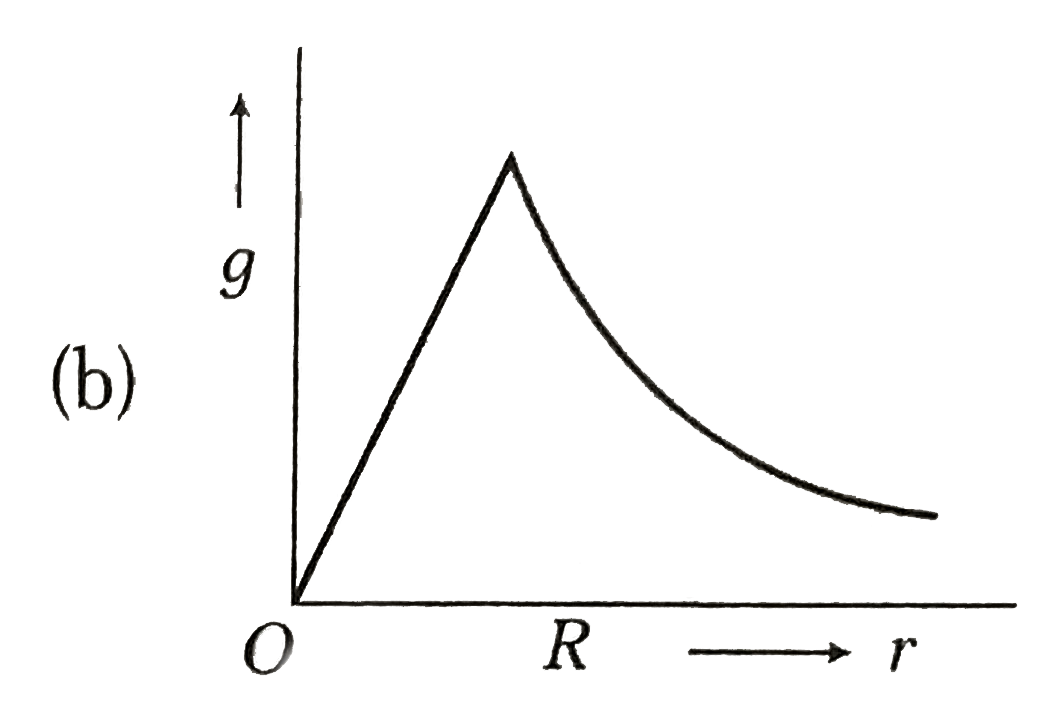 C
C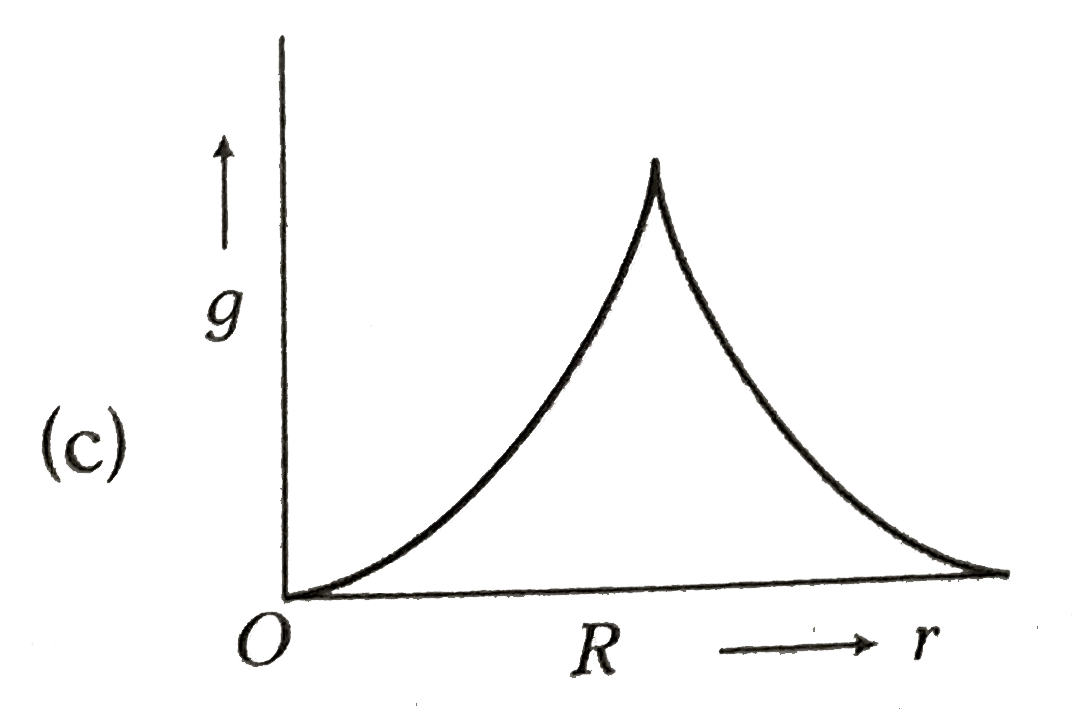 D
D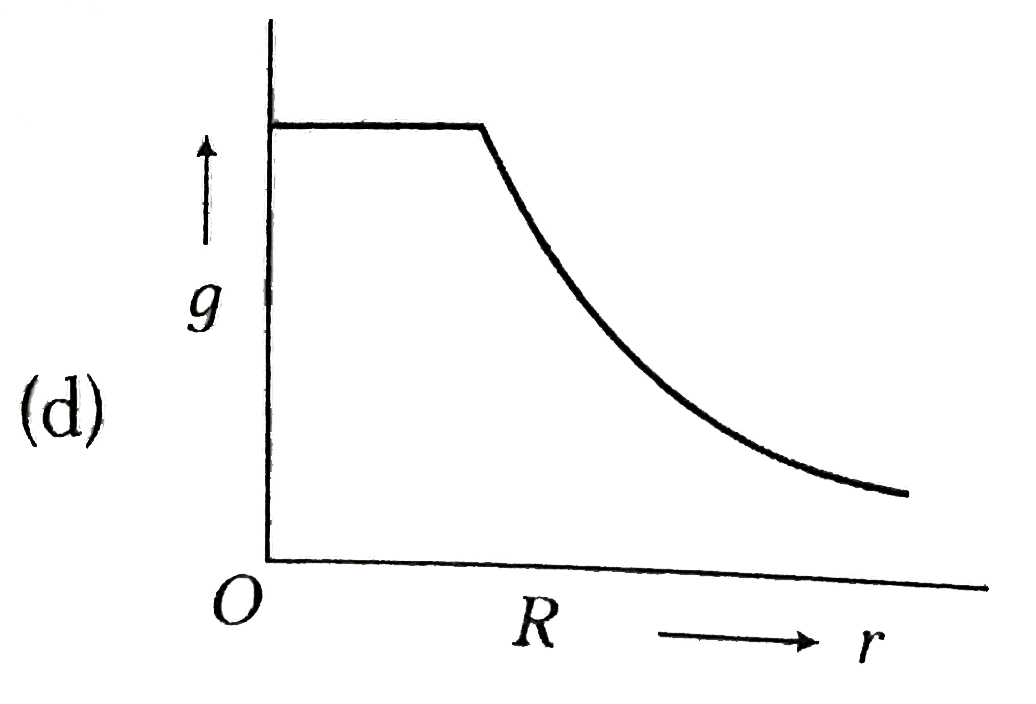
Starting from the centre of the earth having radius R the variation of g (acceleration due to gravity) is shown by
A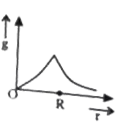 B
B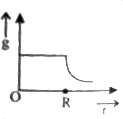 C
C D
D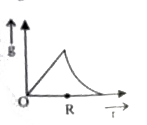
The acceleration due to gravity is _____ at the surface of the earth and ____ at the centre of the earth.
View SolutionIf g is the acceleration due to gravity on the surface of the earth , its value at a height equal to double the radius of the earth is
View SolutionIf the acceleration due to gravity on the surface of earth is g, then the acceleration due to gravity on the surface of a planet whose mass is same as that of earth and radius is twice as that of earth is _________________.
View SolutionIf the acceleration due to gravity on the surface of earth is g, then the acceleration due to gravity on the surface of a planet whose mass is same as that of earth and radius is half as that of earth is _________________.
View SolutionIf g is acceleration due to gravity at the surface of the earth, then its value at a depth of 1/4 of the radius of the earth is
View Solution

