If g is same at a height h and at a depth d, then
R=2d
d=2h
h=d
none
The correct Answer is:B
To solve the problem, we need to analyze the gravitational acceleration g at a height h above the Earth's surface and at a depth d below the Earth's surface. We will derive the relationship between h and d based on the given condition that g is the same at both locations.
1. Understanding Gravitational Acceleration at Height:
The gravitational acceleration gh at a height h above the Earth's surface is given by the formula:
gh=g(1−2hR)
where g is the gravitational acceleration at the surface of the Earth and R is the radius of the Earth.
2. Understanding Gravitational Acceleration at Depth:
The gravitational acceleration gd at a depth d below the Earth's surface is given by the formula:
gd=g(1−dR)
3. Setting the Two Expressions Equal:
Since it is given that gh=gd, we can set the two expressions equal to each other:
g(1−2hR)=g(1−dR)
4. Cancelling g:
We can cancel g from both sides (assuming g≠0):
1−2hR=1−dR
5. Simplifying the Equation:
Subtracting 1 from both sides gives:
−2hR=−dR
Multiplying through by -1 results in:
2hR=dR
6. Removing R:
Since R is a common factor, we can multiply both sides by R (assuming R≠0):
2h=d
7. Final Relationship:
Rearranging gives us the final relationship between depth d and height h:
d=2h
Conclusion:
The correct answer is that the depth d is equal to twice the height h, which corresponds to option 2.
The gravitational acceleration gh at a height h above the Earth's surface is given by the formula:
gh=g(1−2hR)
where g is the gravitational acceleration at the surface of the Earth and R is the radius of the Earth.
The gravitational acceleration gd at a depth d below the Earth's surface is given by the formula:
gd=g(1−dR)
Since it is given that gh=gd, we can set the two expressions equal to each other:
g(1−2hR)=g(1−dR)
We can cancel g from both sides (assuming g≠0):
1−2hR=1−dR
Subtracting 1 from both sides gives:
−2hR=−dR
Multiplying through by -1 results in:
2hR=dR
Since R is a common factor, we can multiply both sides by R (assuming R≠0):
2h=d
Rearranging gives us the final relationship between depth d and height h:
d=2h
The correct answer is that the depth d is equal to twice the height h, which corresponds to option 2.
Topper's Solved these Questions
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Multiple Correct
24 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Assertion- Reasoning
13 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Subjective
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE
1 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
Similar Questions
Knowledge Check
IF the change in the value of g at the height h above the surface of the earth is the same as at a depth x below it, then (both x and h being much smaller than the radius of the earth )
Ax = hBx = 2 hCx = h/2Dx=h2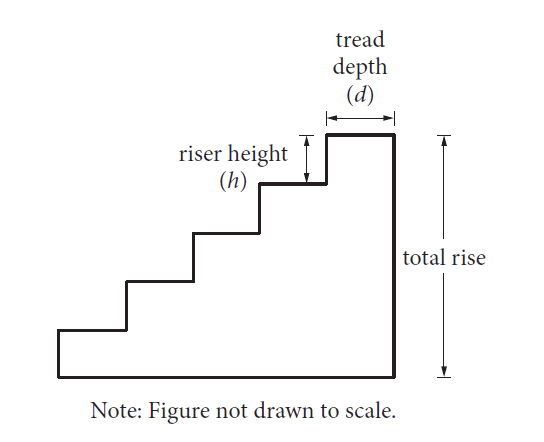
When designing a stairway, an architect can use the riser-tread formula 2h + d = 25, where h is the riser height, in inches, and d is the tread depth, in inches. For any given stairway, the riser heights are the same and the tread depths are the same for all steps in that stairway. The number of steps in a stairway is the number of its risers. For example, there are 5 steps in the stairway in the figure above. The total rise of a stairway is the sum of the riser heights as shown in the figure.
Which of the following expresses the riser height in terms of the tread depth?Ah=12(25+d)Bh=12(25−d)Ch=−12(25+d)Dh=−12(25−d)
If the change in the value of g at a height h above the surface of earth is the same as at a depth d below it (both h and d are much smaller than the radius of the earth), then
View SolutionIf the change in the value of g at a height h above the surface of earth is the same as at a depth d below it (both h and d are much smaller than the radius of the earth), then
View SolutionAt what height, the weight of the body is same as that at same depth from the earth's surface (take, earth's radius = R)
View SolutionWhich of the following statements is true? (A) g is same at all places on the surface of earth. (B) g has its maximum value at the equator. (C) g is less at the earth's surface than at a height above it or a depth below it. (D) g is greater at the poles than at the equator.
View SolutionThe value of 'g' reduces to half of its value at surface of earth at a height 'h', then :-
View SolutionAt what height above the earth's surface, the value of g is same as that at a depth of 100 km ?
View Solution
