If in pervious problem, an additional force F'=100N is applied in vertical direction as shown in figure The friction force acting on the block is
zero
10N
20N
5N
The correct Answer is:d
To solve the problem of finding the friction force acting on the block when an additional force F′=100N is applied in the vertical direction, we can follow these steps:
Step 1: Identify the forces acting on the block
In this scenario, we have:
- The weight of the block mg acting downward.
- The additional force F′=100N acting downward.
- The normal force N acting upward.
- The applied horizontal force F=5N.
Step 2: Write down the equation of motion in the vertical direction
Since the lift is in free fall, the acceleration a of the block is equal to g (acceleration due to gravity). Therefore, we can write the equation of motion in the vertical direction as:
F′+mg−N=ma
Substituting a=g:
100+mg−N=mg
Step 3: Simplify the equation
Rearranging the equation gives:
N=100N
This means that the normal force N acting on the block is equal to the additional force applied downward.
Step 4: Calculate the friction force
The friction force f can be calculated using the formula:
f=μN
Given that the coefficient of friction μ=0.1:
f=0.1×100N=10N
Step 5: Determine the actual friction force
Since the applied horizontal force F=5N is less than the limiting friction force f=10N, the friction force will equal the applied force:
factual=F=5N
Final Answer
The friction force acting on the block is 5N.
---
In this scenario, we have:
- The weight of the block mg acting downward.
- The additional force F′=100N acting downward.
- The normal force N acting upward.
- The applied horizontal force F=5N.
Since the lift is in free fall, the acceleration a of the block is equal to g (acceleration due to gravity). Therefore, we can write the equation of motion in the vertical direction as:
F′+mg−N=ma
Substituting a=g:
100+mg−N=mg
Rearranging the equation gives:
N=100N
This means that the normal force N acting on the block is equal to the additional force applied downward.
The friction force f can be calculated using the formula:
f=μN
Given that the coefficient of friction μ=0.1:
f=0.1×100N=10N
Since the applied horizontal force F=5N is less than the limiting friction force f=10N, the friction force will equal the applied force:
factual=F=5N
The friction force acting on the block is 5N.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
Knowledge Check
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10ms−2)
 A3 NB8 NC4 ND6 N
A3 NB8 NC4 ND6 N
A block system is shown in figure.Frictional force on
View SolutionA block of 50 N is pressed normally against a wall as shown. The frictional force acting on the block is :
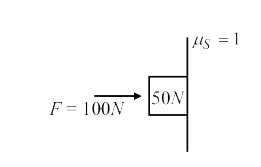 ]
]
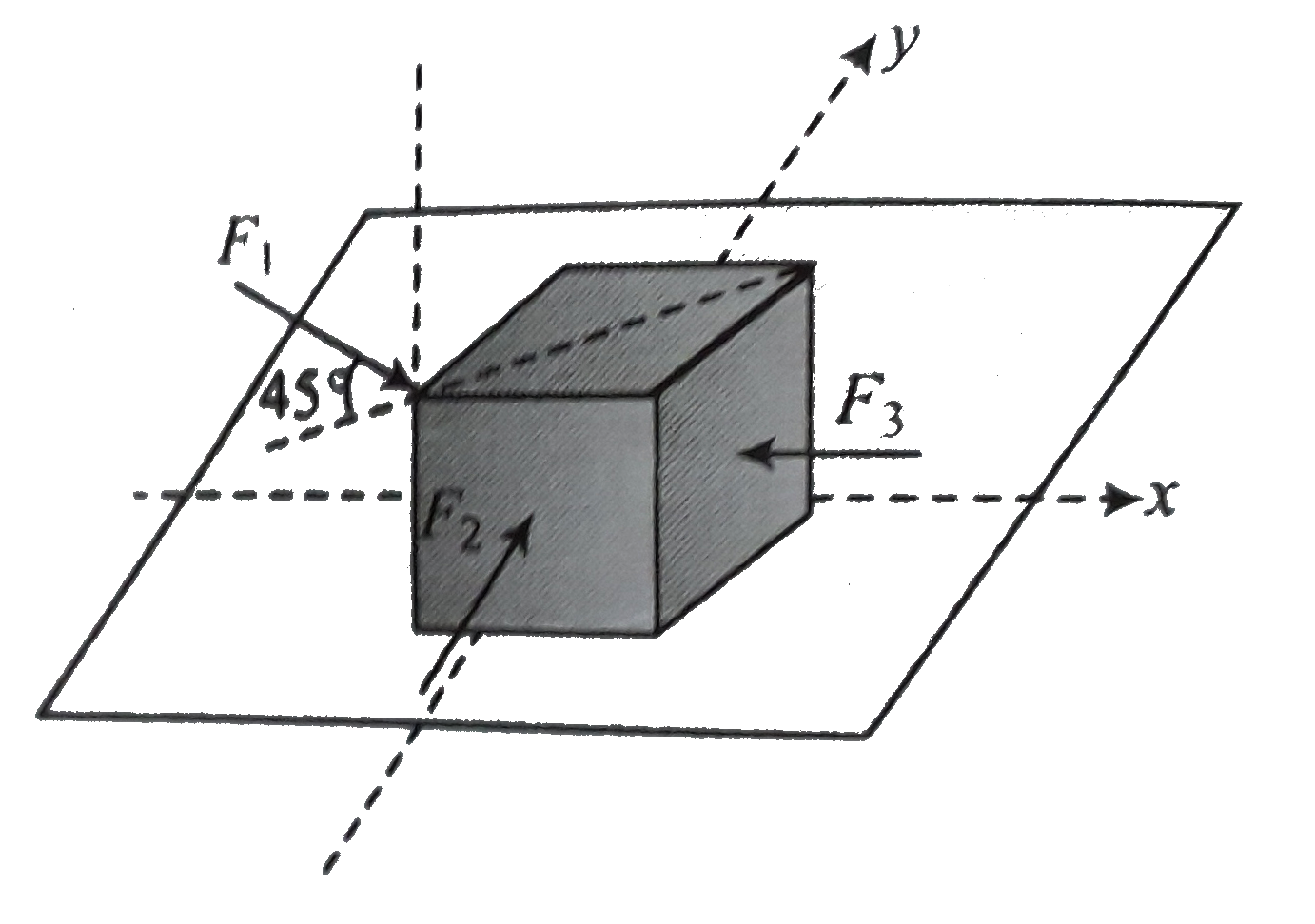
View SolutionA cubical block is experiencing three forces F1=20N acts at angle 45∘with horizontal and lies in diagram plane of the cube F2=30N acts along y- axis and F3=40N acts in x- direction as shown in fig find the friction force acting on the block if it is at rest
View SolutionA force ¯¯¯F=ˆi+4ˆj acts on block shown. The force of friction acting on the block is :
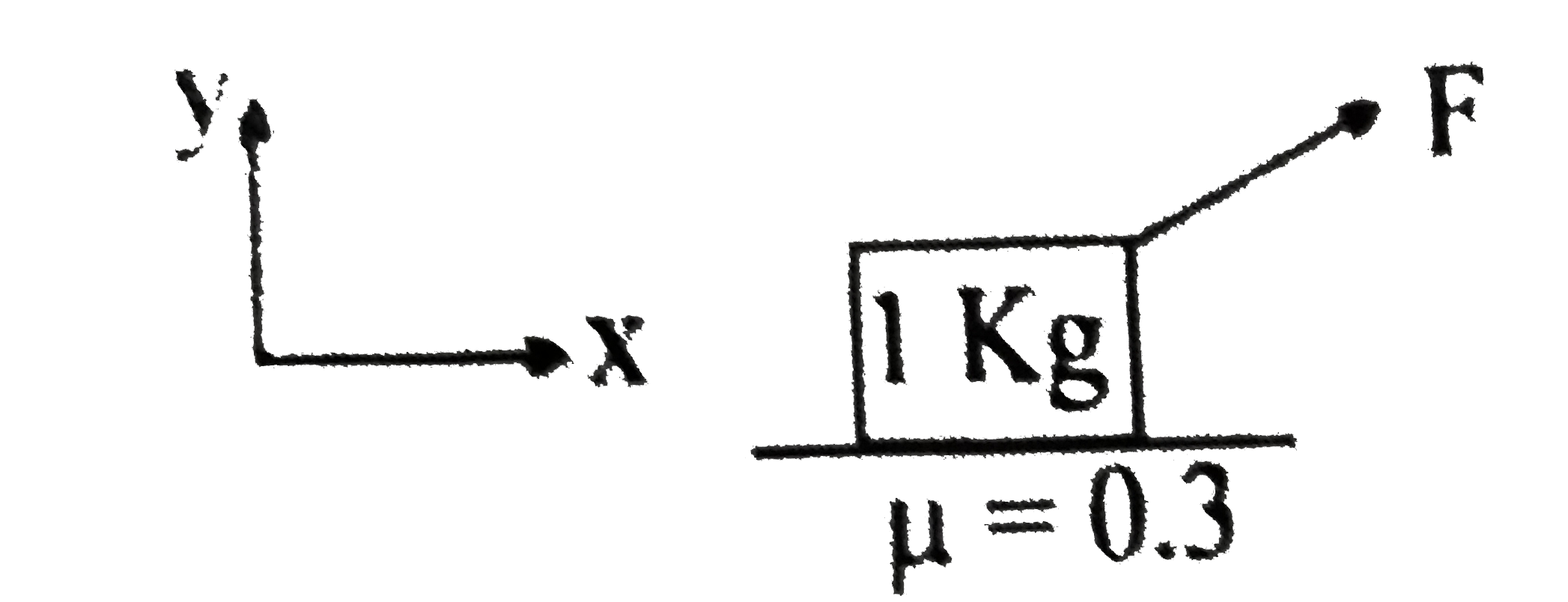
View SolutionA block of mass 20kg is placed on a rough horizontal plane and a horizontal force of 12N is applied. If coefficient of friction is 0.1 the frictional force acting on it is,
View SolutionA body of mass 0.2 kg is pressed into a vertical wall normally with a horizontal force 20 N. Coefficient of friction is 0.9. Another horizontal force of 2N is applied on the body in the vertical plane. The frictional force acting on the body is K√2N. The value of K is
View SolutionPower of a force acting on a block varies with time t as shown in figure. Then, angle between force acting on the block and its velocity is
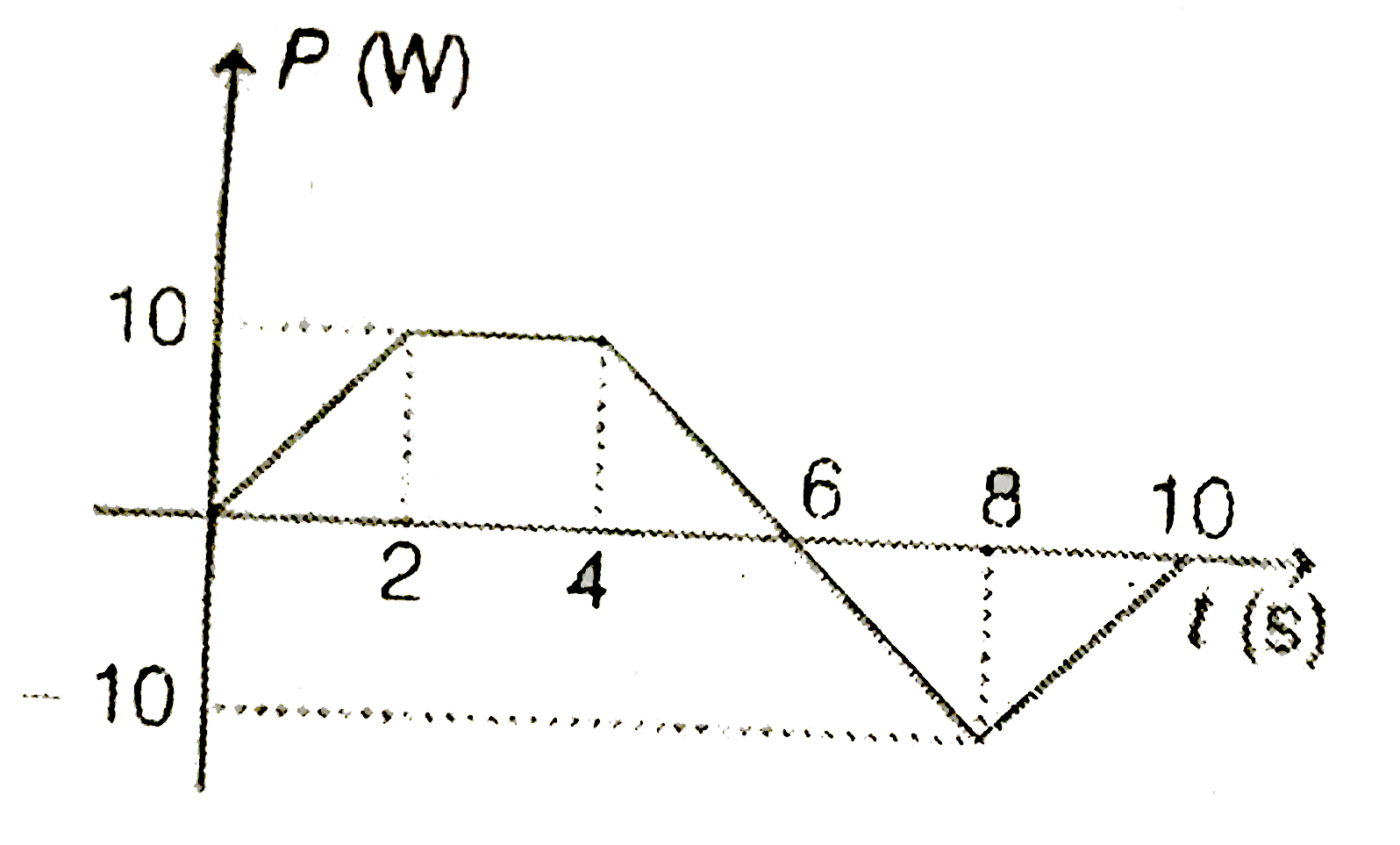
View Solution