If λ1,λ2andλ3 are the wavelengths of the wave giving resonance with the fundamental, first and second overtones respectively of a closed orga pipe Then the ratio of wavelength λ1,λ2andλ3 is
A
1:3:5
B
1:2:3
C
5:3:1
D
1:13:15
Video Solution
Text Solution
The correct Answer is:A
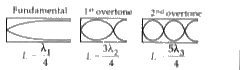
As is clear from figure
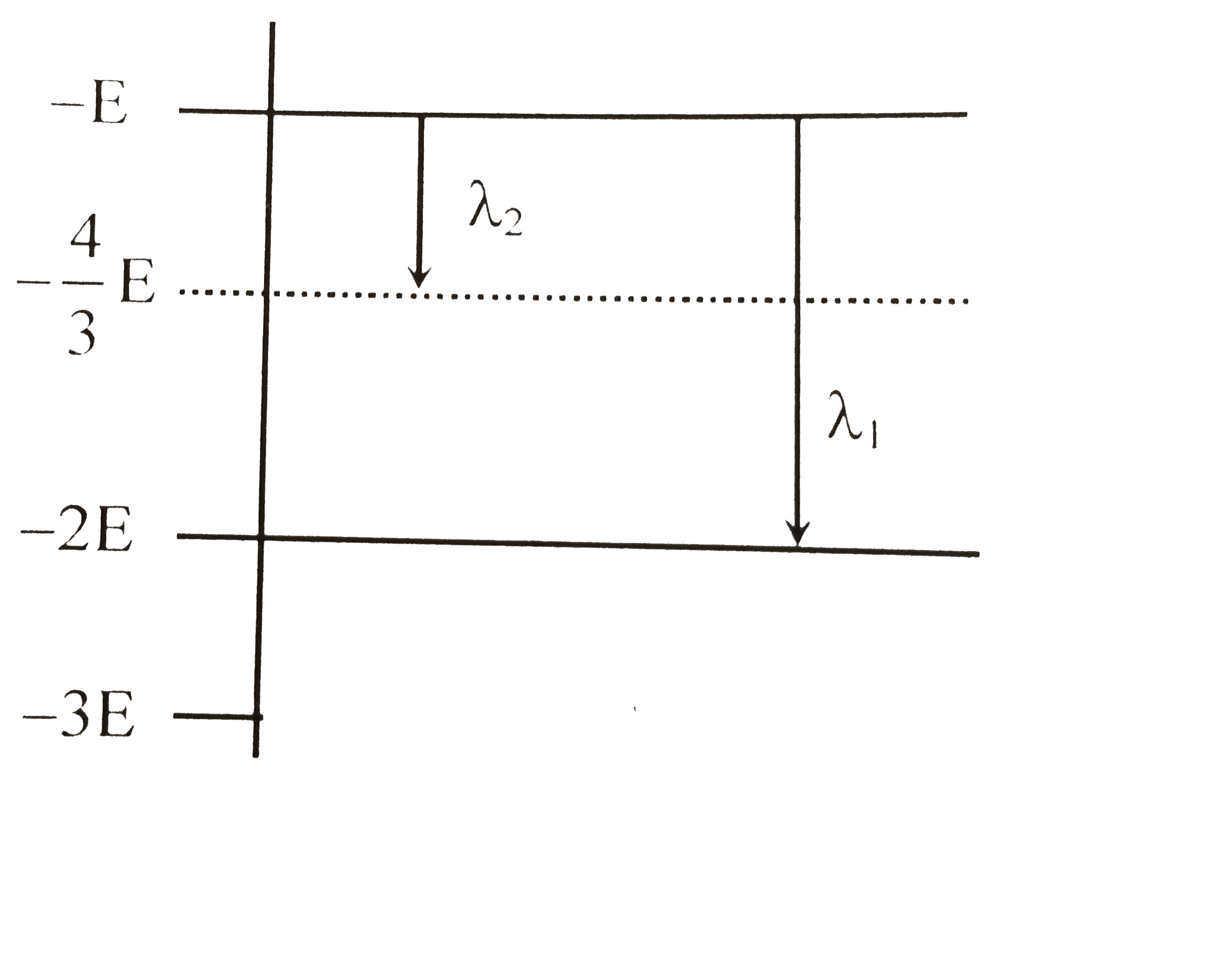
L=λ14orλ1=4L,L=3λ24orλ2=4L3
L=5λ34orλ3=4L5∴λ1:λ2:λ3=1:13:15
|
Topper's Solved these Questions
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - CHECK YOUR NEET VITALS
25 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
- OSCILLATIONS AND WAVES BOOK - MTG GUIDECHAPTER - OSCILLATIONS AND WAVES EXERCISE - AIPMT / NEET MCQs
43 Videos
- MOTION OF SYSTEM OF PARTICLES AND RIGID BODY BOOK - MTG GUIDECHAPTER - MOTION OF SYSTEM OF PARTICLES AND RIGID BODY EXERCISE - AIPMT / NEET (MCQs)
37 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - MTG GUIDECHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - AIPMT / NEET MCQ
14 Videos
Similar Questions
Knowledge Check
If λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
A1:2:3B1:3:5C1:1/2:1/3D1:1/3:1/5If λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
A1:2:3B1:3:5C1:1/2:1/3D1:1/3:1/5If λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
A1:2:3B1:3:5C1:12:13D1:13:15
If λ1andλ2 are the wavelengths of the first members of the Lyman and Paschen series respectively, then λ1:λ2 is
View SolutionIf λ1 and λ2 are the wavelengths of the first members of the Lyman and paschen series respectively, then λ1λ2 is equal to
View Solutionif λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:
View SolutionIn hydrogen atom, if λ1,λ2,λ3 are shortest wavelengths in Lyman, Balmer and Paschen series respectively then λ1:λ2:λ3 equals
View SolutionIf λ1 and λ2 denote the wavelength of de Broglie waves for electrons in the first and second Bohr orbits in a hydrogen atom, the λ1λ2 is equal to
View Solution