If λ1 and λ2 denote the wavelength of de Broglie waves for electrons in the first and second Bohr orbits in a hydrogen atom, the λ1λ2 is equal to
21
12
14
41
The correct Answer is:B
To solve the problem of finding the ratio of the de Broglie wavelengths λ1λ2 for electrons in the first and second Bohr orbits of a hydrogen atom, we can follow these steps:
Step 1: Understand the de Broglie wavelength formula
The de Broglie wavelength λ of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
Step 2: Relate momentum to velocity
For an electron, the momentum p can be expressed as:
p=mv
where m is the mass of the electron and v is its velocity. Therefore, we can rewrite the de Broglie wavelength as:
λ=hmv
Step 3: Establish the relationship between wavelengths in different orbits
Let λ1 be the wavelength of the electron in the first Bohr orbit and λ2 be the wavelength in the second Bohr orbit. From the previous formula, we can say:
λ1=hmv1andλ2=hmv2
Taking the ratio of the two wavelengths gives:
λ1λ2=v2v1
Step 4: Use Bohr's postulate for velocity
According to Bohr's model, the velocity of an electron in the nth orbit is inversely proportional to the principal quantum number n:
v∝1n
Thus, we can express the velocities in terms of the principal quantum numbers:
v1∝1n1andv2∝1n2
Step 5: Substitute the velocities into the wavelength ratio
Substituting the expressions for v1 and v2 into the wavelength ratio, we have:
λ1λ2=v2v1=1n21n1=n1n2
Step 6: Substitute the principal quantum numbers
For the first Bohr orbit, n1=1 and for the second Bohr orbit, n2=2. Therefore:
λ1λ2=n1n2=12
Conclusion
Thus, the ratio of the de Broglie wavelengths for electrons in the first and second Bohr orbits is:
λ1λ2=12
Final Answer
The correct answer is 12.
---
The de Broglie wavelength λ of a particle is given by the formula:
λ=hp
where h is Planck's constant and p is the momentum of the particle.
For an electron, the momentum p can be expressed as:
p=mv
where m is the mass of the electron and v is its velocity. Therefore, we can rewrite the de Broglie wavelength as:
λ=hmv
Let λ1 be the wavelength of the electron in the first Bohr orbit and λ2 be the wavelength in the second Bohr orbit. From the previous formula, we can say:
λ1=hmv1andλ2=hmv2
Taking the ratio of the two wavelengths gives:
λ1λ2=v2v1
According to Bohr's model, the velocity of an electron in the nth orbit is inversely proportional to the principal quantum number n:
v∝1n
Thus, we can express the velocities in terms of the principal quantum numbers:
v1∝1n1andv2∝1n2
Substituting the expressions for v1 and v2 into the wavelength ratio, we have:
λ1λ2=v2v1=1n21n1=n1n2
For the first Bohr orbit, n1=1 and for the second Bohr orbit, n2=2. Therefore:
λ1λ2=n1n2=12
Thus, the ratio of the de Broglie wavelengths for electrons in the first and second Bohr orbits is:
λ1λ2=12
The correct answer is 12.
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct
10 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension
44 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective
16 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
Knowledge Check
The de-Broglie wavelength of an electron in the first Bohr orbit is
Aequal to one- fourth the circumference of the first orbitBequal to half the circumference of first orbitCequal to twice the circumference of first orbit.Dequal to the circumference of the first orbit.the number of de broglie wavelength contained in the second bohr orbit of hydrogen atom is
A1B2C3D4
If λ0 stands for mid-wavelength in the visible region, the de Broglie wavelength for 100 V electrons is nearest to
View SolutionIf λ1 and λ2 are the wavelengths of the first members of the Lyman and paschen series respectively, then λ1λ2 is equal to
View SolutionWhich of the following suggested de-Broglie wavelength(s) is / are possible for electron in a Bohr orbit of Hydrogen atom ?
View Solution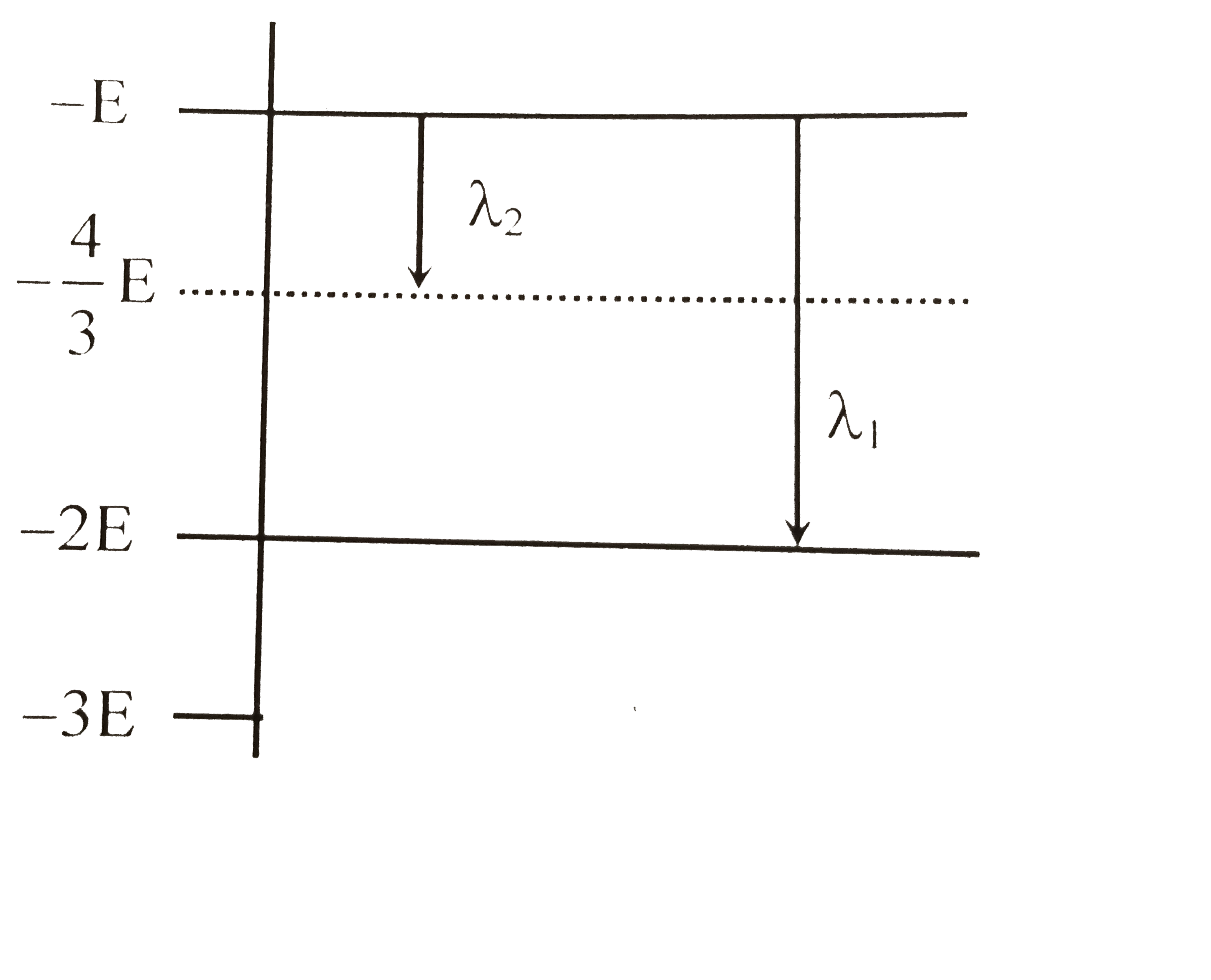
Some energy levels of a molecule are shown in the figure. The ratio of the wavelength r=λ1λ2,is given by:
View SolutionIf λ1,λ2andλ3 are the wavelengths of the wave giving resonance with the fundamental, first and second overtones respectively of a closed organ pipe Then the ratio of wavelength λ1,λ2andλ3 is
View SolutionA uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View Solution
