If ∮sE.ds=0 Over a surface, then
the electric field inside the surface and on it is zero.
the electric field inside the surface is necessarily uniform.
all charges must necessarily be outside the surface.
all of these.
The correct Answer is:C
As ∮→E⋅→ds=qε0,
Where q is charge enclosed by the surface.
when ∮→E⋅→ds=0,q=0
i.e., net charge enclosed by the surface must be zero. Therefore, all other charges must be outside the surface. This is because charges outside the surface do not contribute to the electric flux.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Application Of Gauss Law
9 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - HOTS
1 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTIPSCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Continuous Charge Distribution
5 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTIPSCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assertion And Reason
15 Videos
Similar Questions
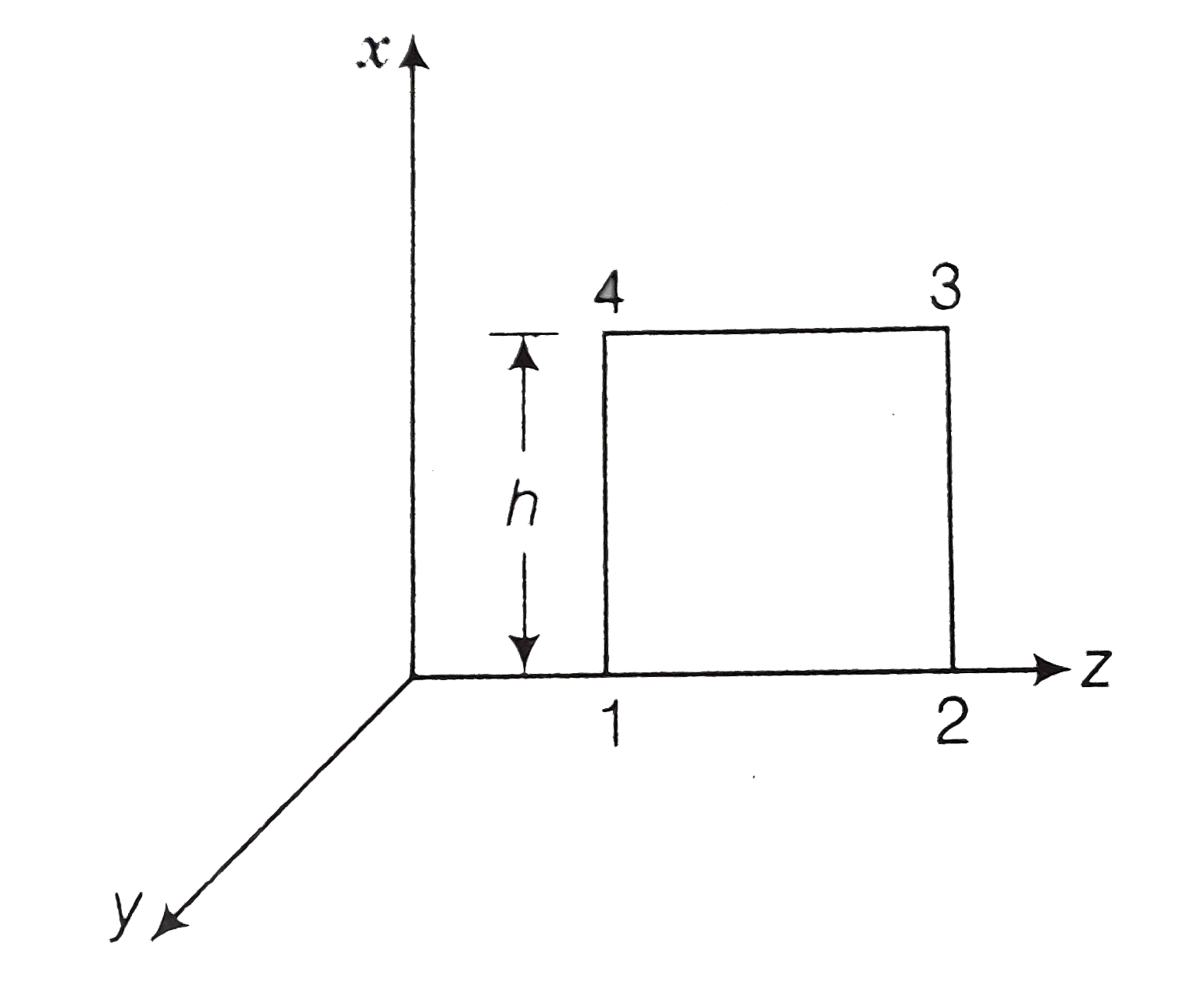
A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0

View Solution
Knowledge Check
STATEMENT -1 : If ∮→E.¯¯¯¯ds over a closed surface is negative,it means the surface encloses a net negative charge.
STATEMENT-2 : We may have a Gaussian surface in which three lines enter and five field lines are coming out.
STATEMENT-3 : The quantity ∮→E.¯¯¯¯ds is independent of the charge distribution inside the surface.AT T TBF F TCF T FDT F FWhen yellow light is incident over a metal surface no electrons are emitted while green light can emit electrons if red light is incident over the surface then
Ano electrons are emittedBmore electronds are emittedCelectrons of higher energy are emittedDelectrons of lower energy are emittedOil spreads over the surface of water whereas water does not spread over the surface of the oil, due to
ASurface tension of water is very highBSurface tension of water is very lowCViscosity of oil is highDViscosity of water is high
If r is the radius, S the surface area and V the volume of a spherical bubble, prove that
(ii) dVdS∞r
View SolutionIf negative charge is enclosed by the surface, then the T. N. E. I. over the surface will be
View SolutionA body is dropped from a height Re (radius of earth) above the earth's surface. It strikes the earth with speed v0, if ve is the escape velocity from earth’s surface, then v0ve is
View SolutionThe law goverening electrostatics is coulomb's law.In priciple coulomb's law can be used to compute electric field due to any charge configuation .In pracitce however it is a formidable task to compute electric field due to uniform charge distributions .For such cases Gauss proposed a theorem which states that
∮¯¯¯E.¯¯¯¯ds=qε0
where ds is an element of area directed across the outward normal for the surface at every point .The integral is called electric flux.Any convenient surface that we choose to evalute the surface integral is called the Gaussian surface.
Gauss throrem in electrostatics states that electric flux ∮(E.ds)=qε0 where S is the Gaussian surface ,the electric field E is due to all the charges
View SolutionAnswer questions on the basis of your understanding of the following paragraph and the related studied concept.
Electric flux, in general , through any surface is defined as per relation:
ϕE=∫→E.→ds , where integration has to be performed over the entire surface through which flux is required. The surface under consideration may be a closed one or an open surface. When flux through a closed surface is required we use a small circular sign on the integration symbol. Thus flux over a closed surface ∮E=∮→E.→ds. it is customary to take the outward normal as positive in this case.
A German physicist Gauss established a fundamental law to find electric flux over a closed surface. As per Gauss' law , the flux of the net electric field through a closed surface equals the net charge enclosed by the surface divided by ∈0.Mathematically ∮→E.→ds=1∈0[qen] , where qcn is the net charge enclosed within the surface. It is possible to derive Gauss' law from Coulomb's laws. Gauss' law can be applied to obtain electric field at a point due to continuous charge distribution for a number of symmetric charge configurations.
Consider a closed surface having certain charges both within and outside as shown. The total electric flux of the given closed surface is : (##U_LIK_SP_PHY_XII_C01_E03_011_Q01.png" width="80%">
View Solution
