If represents radiation pressure , represents the speed of light , and represents radiation energy striking a unit area per second , then non - zero integers such that is dimensionless , find the values of .
To solve the problem, we need to find the values of x,y,z such that the expression PxQyCz is dimensionless. We will start by determining the dimensions of P, Q, and C.
Step 1: Determine the dimensions of P, Q, and C
1. Radiation Pressure P:
- The dimension of pressure is given by force per unit area.
- The dimension of force is (MLT−2).
- Therefore, the dimension of pressure is:
(P)=(F)(A)=(MLT−2)(L2)=(ML−1T−2)
2. Radiation Energy per unit area per second Q:
- The dimension of energy is (ML2T−2).
- Since Q represents energy striking a unit area per second, we have:
(Q)=(E)(A)(T)=(ML2T−2)(L2)(T)=(MT−3)
3. Speed of Light C:
- The dimension of speed is given by distance per unit time:
(C)=(LT−1)
Step 2: Write the expression for PxQyCz
We need to find PxQyCz:
(PxQyCz)=(ML−1T−2)x⋅(MT−3)y⋅(LT−1)z
Step 3: Combine the dimensions
Now we combine the dimensions:
(PxQyCz)=(MxL−xT−2x)⋅(MyT−3y)⋅(LzT−z)
This simplifies to:
(Mx+yL−x+zT−2x−3y−z)
Step 4: Set the dimensions to be dimensionless
For the expression to be dimensionless, the powers of M, L, and T must all equal zero:
1. x+y=0 (for mass)
2. −x+z=0 (for length)
3. −2x−3y−z=0 (for time)
Step 5: Solve the equations
From the first equation:
y=−x
From the second equation:
z=x
Substituting y=−x and z=x into the third equation:
−2x−3(−x)−x=0
−2x+3x−x=0
0=0
This equation is satisfied for any value of x.
Step 6: Choose values for x,y,z
We can choose x=1:
- Then y=−1
- And z=1
Thus, the values are:
x=1,y=−1,z=1
Final Answer:
The values of x,y,z are:
x=1,y=−1,z=1
- The dimension of pressure is given by force per unit area.
- The dimension of force is (MLT−2).
- Therefore, the dimension of pressure is:
(P)=(F)(A)=(MLT−2)(L2)=(ML−1T−2)
- The dimension of energy is (ML2T−2).
- Since Q represents energy striking a unit area per second, we have:
(Q)=(E)(A)(T)=(ML2T−2)(L2)(T)=(MT−3)
- The dimension of speed is given by distance per unit time:
(C)=(LT−1)
(PxQyCz)=(ML−1T−2)x⋅(MT−3)y⋅(LT−1)z
(PxQyCz)=(MxL−xT−2x)⋅(MyT−3y)⋅(LzT−z)
This simplifies to:
(Mx+yL−x+zT−2x−3y−z)
1. x+y=0 (for mass)
2. −x+z=0 (for length)
3. −2x−3y−z=0 (for time)
y=−x
z=x
−2x−3(−x)−x=0
−2x+3x−x=0
0=0
This equation is satisfied for any value of x.
- Then y=−1
- And z=1
x=1,y=−1,z=1
The values of x,y,z are:
x=1,y=−1,z=1
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.26videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Exercise 1.317videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
Similar Questions
Let P represent radiation pressure, c represent speed of light and l represents radiation energy striking a unit area per second, then PxIycz will be dimensionless for
View SolutionIf P represents radiation pressure, C speed of light, and Q radiation energy striking unit area per second and x,y,z are non zero integers, then P^x Q^y C^z is dimensionless. The values of X,y and z are respectively
View SolutionIf p and q vary inversely, find the values of x,y and z.
 View Solution
View SolutionIf p and q vary inversely, find the values of x,y and z.
 View Solution
View SolutionThe points A(x,y),B(y,z) and C(z,x) represents the vertices of a right angled triangle, if
View SolutionIf x,yandz are positive integers such that x<y<zandx+y+z=6, then what is the value of z?
View SolutionIF p and q are in direct variation of x, y and z in the table given below:
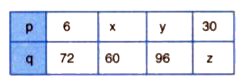 View Solution
View SolutionIf yz+zx+xy=12,andx,y,z are positive values, find the greatest value of xyz.
View SolutionIf the equation px2+(2−q)xy+3y2−6qx+30y+6q=0 represents a circle, then find the values of p and q.
View SolutionIn the given figure, l || m and p || q. Find the value of x,y,z,t.
View Solution

