If P(r) is the radial probability density for a hydrogen atom then the probability that the separation of the electron and proton is between r and r+ dr is
The correct Answer is:a
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS (More than One Correct Choice Type)15videos
HYDROGEN ATOM
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)9videos
HYDROGEN ATOM
- BOOK - RESNICK AND HALLIDAYCHAPTER - HYDROGEN ATOMEXERCISE - PROBLEMS36videos
HYDROGEN ATOM
- BOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)5videos
HEAT-MEASUREMENT AND TRANSFER
- BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Integer Type)6videos
INTERFERENCE AND DIFFRACTION
Similar Questions
Knowledge Check
- Question 1 - Select One
According to Bohr's theory of a hydrogen atom, choose the correct statement, if it is given that the potential energy between electron and proton at a distance r is −ke23r3
Aenergy in the nth orbit is proportional to n5Benergy is proportional to m−3 (m = mass of electron)Cenergy in the nth orbit is proportional to n−2Denergy is proportional to m3 (m= mass of electron) - Question 2 - Select One
The Schrodinger wave equation for H-atom is
∇2Ψ=8π2mh2(E−V)Ψ=0
Where ∇2=∂2∂x2+∂2∂y2+∂2∂z2
E = Total energy and V=potential energy wave function Ψ(rθϕ)R(r)Θ(θ)Φ(ϕ)
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. Θ and Φ are angular wave function. R2 is known as radial probability density and 4πr2R2dr is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
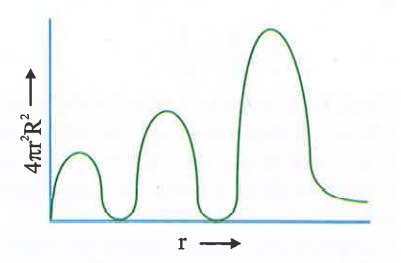
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
Ψ1s=√1πaa0e−zr/a0
Ψ2s=(Z2a0)½(1−Zra0)e−Zra0
The plot of radial probability function 4πr2R2 aganist r will be:
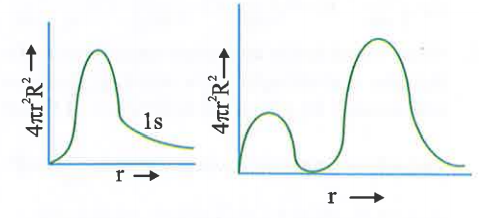
Answer the following questions:
The following graph is plotted for ns-orbitals
The value of 'n' will be:A1B2C3D4 - Question 3 - Select One
The total energy (E) of the electron is an orbit of radius r in hydrogen atom is
Ae28πε0rB−e24πε0rC−e28πε0rDzero
Calculate the radial probability density P(r) for the hydro- gen atom in its ground state at (a) r = 0, (b) r = a, and (c) r= 2a, where a is the Bohr radius.
View SolutionThe variation of radial probability density R2 (r) as a function of distance r of the electron from the nucleus for 3p orbital:
View SolutionWhat is the probability that an electron in the ground state of the hydrogen atom will be found between two spherical shells whose radii are r and r+Δr, (a) if r = 0.500a and Δr = 0.010a and (b) if r = 1.00a and Δr = 0.01a, where a is the Bohr radius? (Hint: Δr is small enough to permit the radial probability density to be taken to be constant between r and r+Δr.)
View SolutionThe total energy (E) of the electron is an orbit of radius r in hydrogen atom is
View SolutionAssertion. The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical
Reason. Probability density is Ψ2 whereas radial probability function represents probability of finding the electron in a shell of thickness dr.View Solution

