Assertion. The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical
Reason. Probability density is Ψ2 whereas radial probability function represents probability of finding the electron in a shell of thickness dr.
If both assertion and reason are true, and reason is the true explanation of the assertion
If both assertion and reason are true, but reason is not the true explanation of the assertion
If assertion is true, but reason is false
If both assertion and reason are false
The correct Answer is:A
To solve the question, we need to analyze the assertion and reason provided:
Assertion: The plots of probability density and radial probability function versus distance r from the nucleus for any particular orbital are not identical.
Reason: Probability density is Ψ2 whereas radial probability function represents the probability of finding the electron in a shell of thickness dr.
1. Understanding Probability Density:
- Probability density for an electron in an orbital is given by the square of the wave function, Ψ2. This function describes the likelihood of finding an electron at a specific point in space.
- The plot of Ψ2 versus distance r from the nucleus shows how the probability density changes with distance.
Hint: Remember that Ψ2 gives the probability density at a point in space.
2. Understanding Radial Probability Function:
- The radial probability function, on the other hand, is defined as 4πr2Ψ2. This function accounts for the volume element in spherical coordinates, which is important because electrons can be found in any direction around the nucleus.
- The radial probability function represents the probability of finding an electron within a spherical shell of thickness dr at a distance r from the nucleus.
Hint: The radial probability function incorporates the geometry of space, which is why it includes the factor 4πr2.
3. Comparing the Two Functions:
- When we plot both Ψ2 and 4πr2Ψ2 against r, we will see that the shapes of these plots are different. The probability density plot shows how likely it is to find an electron at a specific point, while the radial probability function shows how likely it is to find the electron within a spherical shell.
- Therefore, the assertion that these plots are not identical is correct.
Hint: Visualize the graphs: one is a function of distance, while the other is a function of the volume around that distance.
4. Evaluating the Reason:
- The reason provided states that probability density is Ψ2 and that the radial probability function represents the probability of finding the electron in a shell of thickness dr. This statement is accurate and correctly explains why the two plots differ.
- Thus, the reason supports the assertion.
Hint: Check if the reason logically follows from the assertion.
5. Conclusion:
- Both the assertion and the reason are true, and the reason correctly explains the assertion. Therefore, the correct answer is that both the assertion and reason are true, and the reason is the correct explanation for the assertion.
Final Answer: Both the assertion and reason are true, and the reason is the correct explanation for the assertion.
- Probability density for an electron in an orbital is given by the square of the wave function, Ψ2. This function describes the likelihood of finding an electron at a specific point in space.
- The plot of Ψ2 versus distance r from the nucleus shows how the probability density changes with distance.
- The radial probability function, on the other hand, is defined as 4πr2Ψ2. This function accounts for the volume element in spherical coordinates, which is important because electrons can be found in any direction around the nucleus.
- The radial probability function represents the probability of finding an electron within a spherical shell of thickness dr at a distance r from the nucleus.
- When we plot both Ψ2 and 4πr2Ψ2 against r, we will see that the shapes of these plots are different. The probability density plot shows how likely it is to find an electron at a specific point, while the radial probability function shows how likely it is to find the electron within a spherical shell.
- Therefore, the assertion that these plots are not identical is correct.
- The reason provided states that probability density is Ψ2 and that the radial probability function represents the probability of finding the electron in a shell of thickness dr. This statement is accurate and correctly explains why the two plots differ.
- Thus, the reason supports the assertion.
- Both the assertion and the reason are true, and the reason correctly explains the assertion. Therefore, the correct answer is that both the assertion and reason are true, and the reason is the correct explanation for the assertion.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - STRUCTURE OF ATOMEXERCISE - Competition Focus (JEE (Main and Advanced)/Medical Entrance (IX. Assertion And Reason Type Questions (Type I))5videos
STRUCTURE OF ATOM
- BOOK - PRADEEPCHAPTER - STATES OF MATTER: SOLID MATTEREXERCISE - COMPETITION FOCUS (ASSERTION-REASON)17videos
STATES OF MATTER: SOLID MATTER
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - MULTIPLE CHOICE QUESTION ( BASED ON PRACTICAL CHEMISTRY)3videos
THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The zero probability of finding the electron in dx2−y2 orbital is
Aon two opposite side of nucleus along x-axis.Bin the nucleusCsame on all the sides around the nucleus.DNone of these - Question 2 - Select One
The zero probability of finding the electron in dx2−y2 orbital is
Aon two opposite side of nucleus along x-axis.Bin the nucleusCsame on all the sides around the nucleus.DNone of these - Question 3 - Select One
The zero probability of finding the electron in dx2−y2 orbital is
Aon two opposite side of nucleus along x-axis.Bin the nucleusCsame on all the sides around the nucleus.DNone of these
ψ2 ,( psi) the wave function resperesents the probability of finding electron . Its value depends :
View SolutionThe orbital having zero probability of finding electron on the surface of nucleus is
View SolutionThe probability of finding elercrtron at a distance r form the nucleus for H or H like atom is :
View SolutionThe Schrodinger wave equation for H-atom is
∇2Ψ=8π2mh2(E−V)Ψ=0
Where ∇2=∂2∂x2+∂2∂y2+∂2∂z2
E = Total energy and V=potential energy wave function Ψ(rθϕ)R(r)Θ(θ)Φ(ϕ)
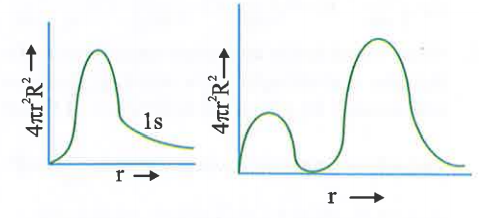
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. Θ and Φ are angular wave function. R2 is known as radial probability density and 4πr2R2dr is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
Ψ1s=√1πaa0e−zr/a0
Ψ2s=(Z2a0)½(1−Zra0)e−Zra0
The plot of radial probability function 4πr2R2 aganist r will be:
Answer the following questions:
The following graph is plotted for ns-orbitals
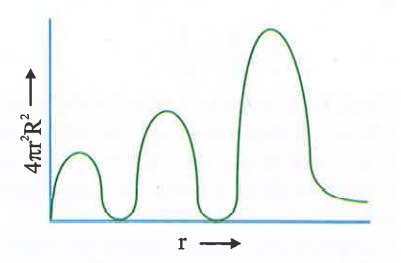
The value of 'n' will be:View SolutionThe Schrodinger wave equation for H-atom is
∇2Ψ=8π2mh2(E−V)Ψ=0
Where ∇2=∂2∂x2+∂2∂y2+∂2∂z2
E = Total energy and V=potential energy wave function Ψ(rθϕ)R(r)Θ(θ)Φ(ϕ)
R is radial wave function which is function of ''r'' only, where r is the distance from nucleus. Θ and Φ are angular wave function. R2 is known as radial probability density and 4πr2R2dr is known as radial probability function i.e., the probability of finding the electron is spherical shell of thickness dr.
Number of radial node =n -l - 1
Number of angular node = l
For hydrogen atom, wave function for 1s and 2s-orbitals are:
Ψ1s=√1πaa0e−zr/a0
Ψ2s=(Z2a0)½(1−Zra0)e−Zra0
The plot of radial probability function 4πr2R2 aganist r will be:

Answer the following questions:
The value of radius 'r' for 2s atomic orbital of H-atom at which the radial node will exist may be given as:View Solution

