If the charge is placed at the center of one side, flux through the cube is qnε0 where .n. is
The correct Answer is:4
To solve the problem, we will use Gauss's law, which states that the electric flux through a closed surface is proportional to the charge enclosed by that surface.
1. Understanding the Setup:
We have a cube and a charge Q placed at the center of one of its faces. We need to find the flux through the entire cube.
2. Applying Gauss's Law:
According to Gauss's law, the total electric flux Φ through a closed surface is given by:
Φ=Qencϵ0
where Qenc is the total charge enclosed by the surface and ϵ0 is the permittivity of free space.
3. Determining the Charge Enclosed:
Since the charge Q is located at the center of one face of the cube, we need to determine how much of this charge is effectively enclosed by the cube. The cube can be thought of as being divided into six equal parts, with only one part containing the charge.
4. Calculating the Flux through the Cube:
The flux through the entire cube can be calculated as:
Φcube=Q6ϵ0
This is because only one-sixth of the charge Q is effectively enclosed by the cube.
5. Relating to the Given Expression:
According to the problem, the flux through the cube is also given by:
Φcube=Qnϵ0
where n is the value we need to find.
6. Setting the Equations Equal:
Now we can set the two expressions for the flux equal to each other:
Q6ϵ0=Qnϵ0
7. Solving for n:
By simplifying the equation, we can cancel Q and ϵ0 (assuming Q≠0 and ϵ0≠0):
16=1n
Therefore, we find:
n=6
Final Answer:
The value of n is 6.
We have a cube and a charge Q placed at the center of one of its faces. We need to find the flux through the entire cube.
According to Gauss's law, the total electric flux Φ through a closed surface is given by:
Φ=Qencϵ0
where Qenc is the total charge enclosed by the surface and ϵ0 is the permittivity of free space.
Since the charge Q is located at the center of one face of the cube, we need to determine how much of this charge is effectively enclosed by the cube. The cube can be thought of as being divided into six equal parts, with only one part containing the charge.
The flux through the entire cube can be calculated as:
Φcube=Q6ϵ0
This is because only one-sixth of the charge Q is effectively enclosed by the cube.
According to the problem, the flux through the cube is also given by:
Φcube=Qnϵ0
where n is the value we need to find.
Now we can set the two expressions for the flux equal to each other:
Q6ϵ0=Qnϵ0
By simplifying the equation, we can cancel Q and ϵ0 (assuming Q≠0 and ϵ0≠0):
16=1n
Therefore, we find:
n=6
The value of n is 6.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - I (MAIN) STRAIGHT OBJECTIVE TYPE QUESTION)19videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -IV ELECTRIC POTENTIAL & POTENTIAL ENERGY) (LEVEL - II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTION)28videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROSTATICSEXERCISE - PRACTICE SHEET (EXERCISE -III ELECTRO FLUX & GAUSS.S LAW) (LEVEL - I (ADVANCED) MATRIX MATCHING TYPE QUESTIONS1videos
ELECTROSTATICS
- BOOK - AAKASH SERIESCHAPTER - ELECTROMAGNETICSEXERCISE - ADDITIONAL EXERCISE13videos
ELECTROMAGNETICS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS10videos
ELEMENTS OF VECTORS
Similar Questions
A point charge Q is kept at point 'A' the flux through the inclined surface of cone is 3Q5ε0. Now another charge −Q is also placed at point B. If net flux through the inclined surface nQ5ε0 is Find n.
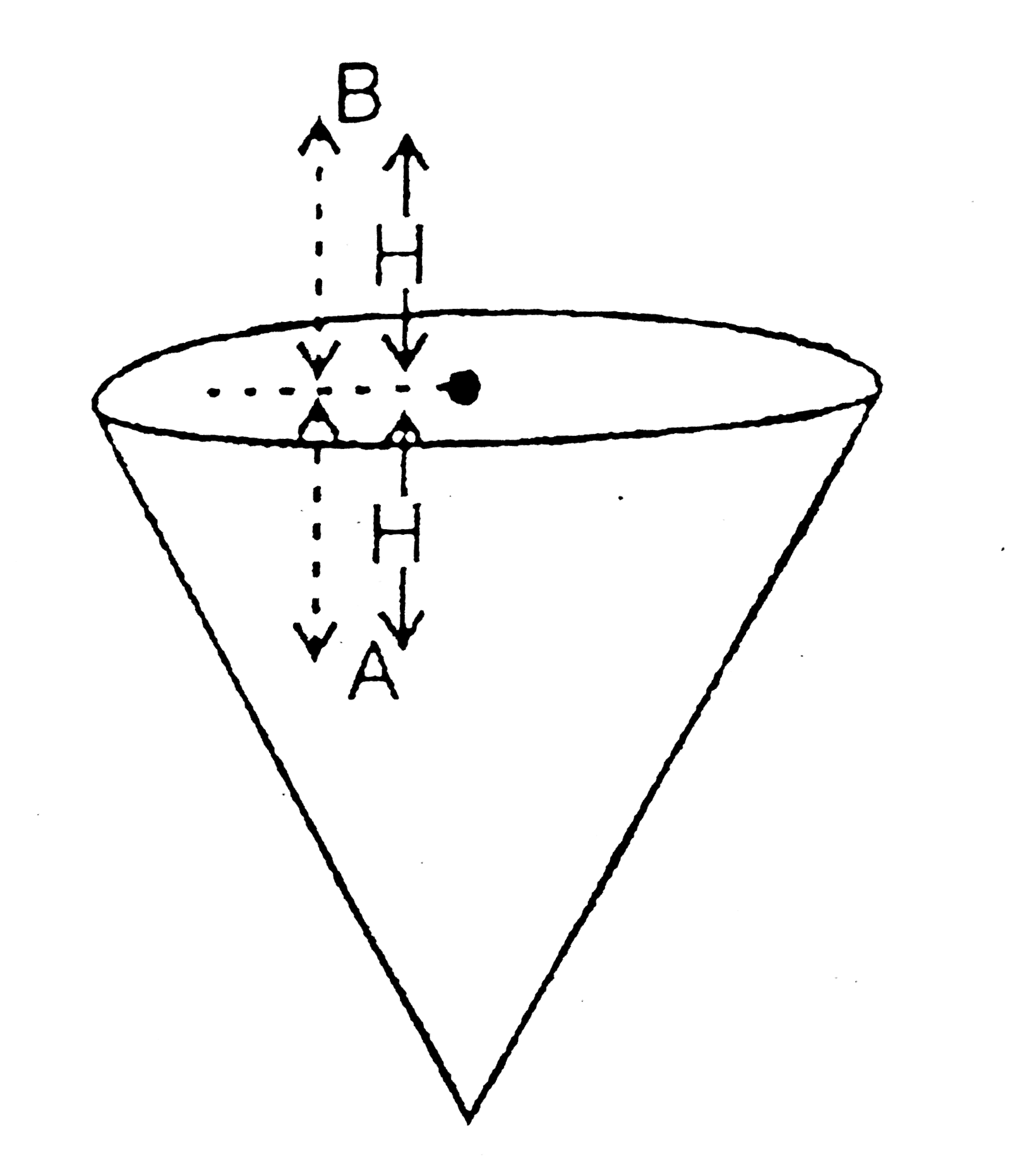 View Solution
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA point charge Q is placed at the corner of a square of side a. Find the flux through the square.
View SolutionA charge q is placed at the centre of a cube. What is the electric flux passing through the cube?
View SolutionA charge Q is situated at the centre of a cube. The electric flux through one of the faces of the cube is
View SolutionA charge is placed at the centre of cube of side a then flux linked with one of its given faces will be
View SolutionA point charge +q is placed at the centre of curvature of a hemisphere. Find flux through the hemispherical surface.
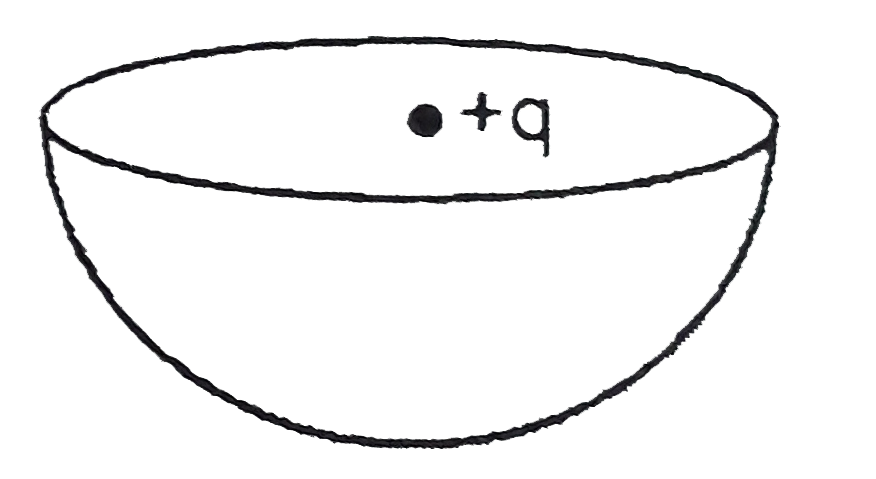 View Solution
View SolutionIf a point charge q is placed at one corner of a cube, what is the flux linked with the cube?
View SolutionIf a point charge q is placed at the centre of a cube.
What is the flux linked (a) with the cube? (b) with each face of the cube?View Solution

