A charge Q is situated at the centre of a cube. The electric flux through one of the faces of the cube is
Q/ε0
Q/2ε0
Q/4ε0
Q/6ε0
The correct Answer is:D
To find the electric flux through one face of a cube when a charge Q is situated at the center, we can use Gauss's Law. Here’s a step-by-step solution:
Step 1: Understand Gauss's Law
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ε0:
Φ=Qε0
Step 2: Identify the Closed Surface
In this case, the closed surface is the cube, and the charge Q is located at its center. Since the cube is symmetric, the electric flux will be uniformly distributed across all six faces of the cube.
Step 3: Calculate Total Electric Flux
Using Gauss's Law, the total electric flux through the entire cube is:
Φtotal=Qε0
Step 4: Distribute the Flux Across the Faces
Since the cube has six faces and the flux is uniformly distributed, the electric flux through one face of the cube can be calculated by dividing the total flux by the number of faces:
Φone face=Φtotal6=Q6ε0
Step 5: Conclusion
Thus, the electric flux through one face of the cube is:
Φone face=Q6ε0
Final Answer
The electric flux through one of the faces of the cube is Q6ε0.
---
Gauss's Law states that the total electric flux Φ through a closed surface is equal to the charge enclosed Q divided by the permittivity of free space ε0:
Φ=Qε0
In this case, the closed surface is the cube, and the charge Q is located at its center. Since the cube is symmetric, the electric flux will be uniformly distributed across all six faces of the cube.
Using Gauss's Law, the total electric flux through the entire cube is:
Φtotal=Qε0
Since the cube has six faces and the flux is uniformly distributed, the electric flux through one face of the cube can be calculated by dividing the total flux by the number of faces:
Φone face=Φtotal6=Q6ε0
Thus, the electric flux through one face of the cube is:
Φone face=Q6ε0
The electric flux through one of the faces of the cube is Q6ε0.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Exercise57videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Exercise-I80videos
ELECTRIC CHARGES AND FIELDS
- BOOK - AAKASH SERIESCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - PRACTICE EXERCISEX42videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - AAKASH SERIESCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - PROBLEMS (LEVEL-II)26videos
ELECTRIC FIELD AND POTENTIAL
Similar Questions
A charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA charge Q is situated at the corner of a cube, the electric flux passing through all the six faces of the cube is :
View SolutionA charge q is placed at the centre of a cube. What is the electric flux passing through the cube?
View SolutionCharge of 2 C is placed at the centre of a cube. What is the electric flux passing through one face ?
View SolutionA point charge q is placed at the centre of a cube. What is the flux linked.
a with all the faces of the cube?
b. with each face of the cube?
c. if charge is not at the centre, then what will be the answer of parts a and b ?View SolutionA point charge q is placed at the centre of a cube. What is the flux linked.
a with all the faces of the cube?
b. with each face of the cube?
c. if charge is not at the centre, then what will be the answer of parts a and b ?View SolutionEight point charges (can be assumed as small spheres uniformly charged and their centres at the corner of the cube) having values q each are fixed at vertices of a cube. The electric flux through square surface ABCD of the cube is
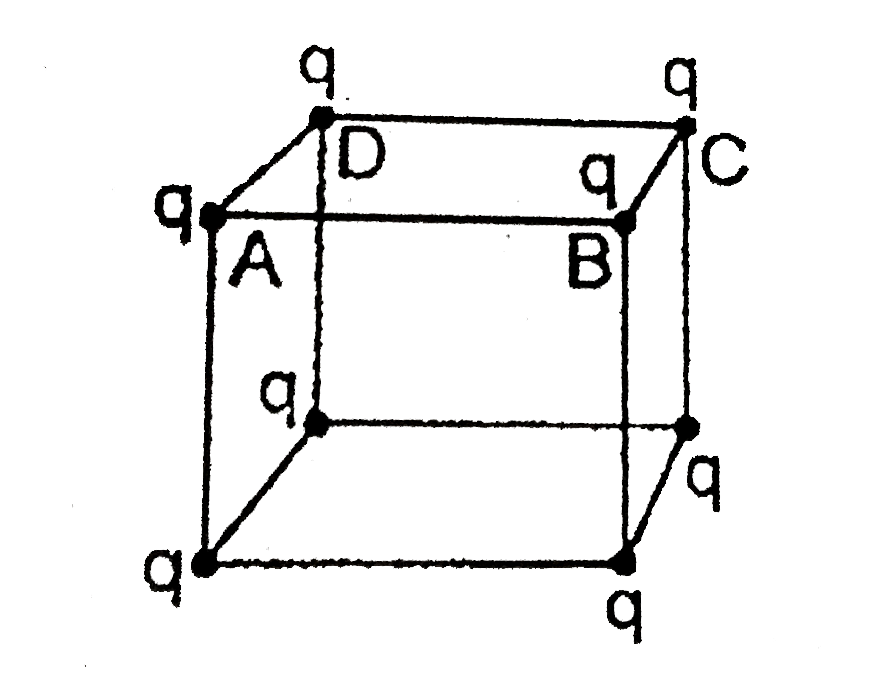 View Solution
View SolutionEight point charges (can be assumed as small spheres uniformly charged and their centres at the corner of the cube) having values q each are fixed at vertices of a cube. The electric flux through square surface ABCD of the cube is
 View Solution
View SolutionA very small sphere having a charge q, uniformly distributed throughout its volume, is placed at the vertex of a cube of side a. The electric flux through the cube is
View Solution

