If the trajectory of a body is parabolic in one frame, can it be parabolic in another frame that moves with a constant velocity with respect to the first frame? If not, what can it be?
To solve the question, we need to analyze the trajectory of a body in different frames of reference, particularly when one frame is moving with a constant velocity relative to another.
1. Understanding the Initial Condition:
- We start with a body whose trajectory is parabolic in one inertial frame (let's call it Frame A). This typically occurs when the body is subject to uniform gravitational acceleration, like a projectile.
2. Defining the Second Frame:
- Now, consider another frame (Frame B) that moves with a constant velocity v relative to Frame A. This means that Frame B is also an inertial frame, as it is moving at a constant velocity without any acceleration.
3. Applying the Principle of Invariance:
- According to Newton's laws, the laws of motion are the same in all inertial frames. Therefore, the equations of motion describing the trajectory of the body will hold true in Frame B as well.
4. Transforming the Equations of Motion:
- In Frame A, the trajectory of the body can be described by the equations of motion for projectile motion, which is typically a quadratic equation (parabolic).
- When we switch to Frame B, we need to account for the constant velocity v of Frame B. The motion in Frame B can be described by transforming the coordinates from Frame A to Frame B.
5. Resulting Trajectory in Frame B:
- The transformation will still yield a quadratic equation, which means that the trajectory will remain parabolic in Frame B as well. This is because the addition of a constant velocity does not change the nature of the acceleration acting on the body (which is still gravitational).
6. Conclusion:
- Therefore, the trajectory of the body can indeed be parabolic in both frames (Frame A and Frame B) that move with a constant velocity relative to each other.
Final Answer:
Yes, the trajectory can be parabolic in another frame that moves with a constant velocity with respect to the first frame.
---
- We start with a body whose trajectory is parabolic in one inertial frame (let's call it Frame A). This typically occurs when the body is subject to uniform gravitational acceleration, like a projectile.
- Now, consider another frame (Frame B) that moves with a constant velocity v relative to Frame A. This means that Frame B is also an inertial frame, as it is moving at a constant velocity without any acceleration.
- According to Newton's laws, the laws of motion are the same in all inertial frames. Therefore, the equations of motion describing the trajectory of the body will hold true in Frame B as well.
- In Frame A, the trajectory of the body can be described by the equations of motion for projectile motion, which is typically a quadratic equation (parabolic).
- When we switch to Frame B, we need to account for the constant velocity v of Frame B. The motion in Frame B can be described by transforming the coordinates from Frame A to Frame B.
- The transformation will still yield a quadratic equation, which means that the trajectory will remain parabolic in Frame B as well. This is because the addition of a constant velocity does not change the nature of the acceleration acting on the body (which is still gravitational).
- Therefore, the trajectory of the body can indeed be parabolic in both frames (Frame A and Frame B) that move with a constant velocity relative to each other.
Yes, the trajectory can be parabolic in another frame that moves with a constant velocity with respect to the first frame.
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - NUMERICAL EXERCISE (LEVEL -1)
33 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - NUMERICAL EXERCISE (LEVEL -2)
19 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - SHORT ANSWER TYPE QUESTIONS
6 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-3 (Circular Motion)
7 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
Similar Questions
A frame will be inertial, if it moves with respect to another inertial frame with a constant :-
View SolutionFrames moving uniformly with respect to an inertial frame are
View SolutionPseudo force with respect to a frame moving with constant velocity is zero. Is this statement true or false?
View SolutionA particle is found to be at rest when seen from a frame S1 and moving with a constant velocity when seen from another frame S2. Select the possible options :
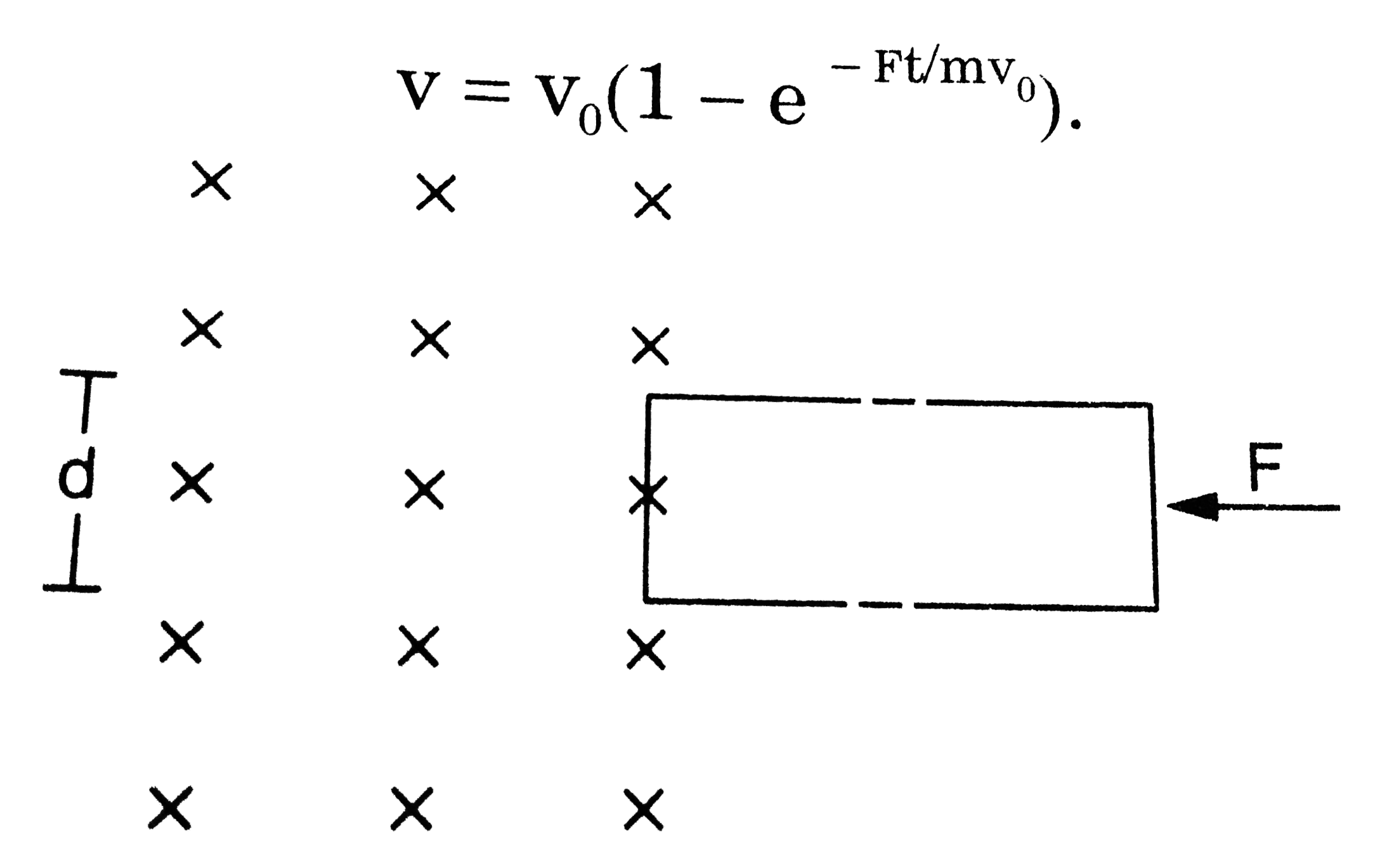
View SolutionThe rectangualr wire- frame, shown in has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t =0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. find this velocity v0. (c) show that the velocity at tiem t is given by v=v0(1−e−Ftmv0.
View SolutionStatement I: A particle is found to be a rest when seen from a frame S1 and moving with a constant velocity when seen from another frame S2. We can say both the frames are inertial.
Statement II: All frames moving uniformly with respect to an inertial frame are themselves inertial.
View SolutionAssertion:− A particle on earth found to be at rest when seen from a frame U1 and moving with a constant velocity when seen from another frame U2. Then both frames may be non−inertial.
Reason :− A reference frame attached to the earth must be an inertial frame.
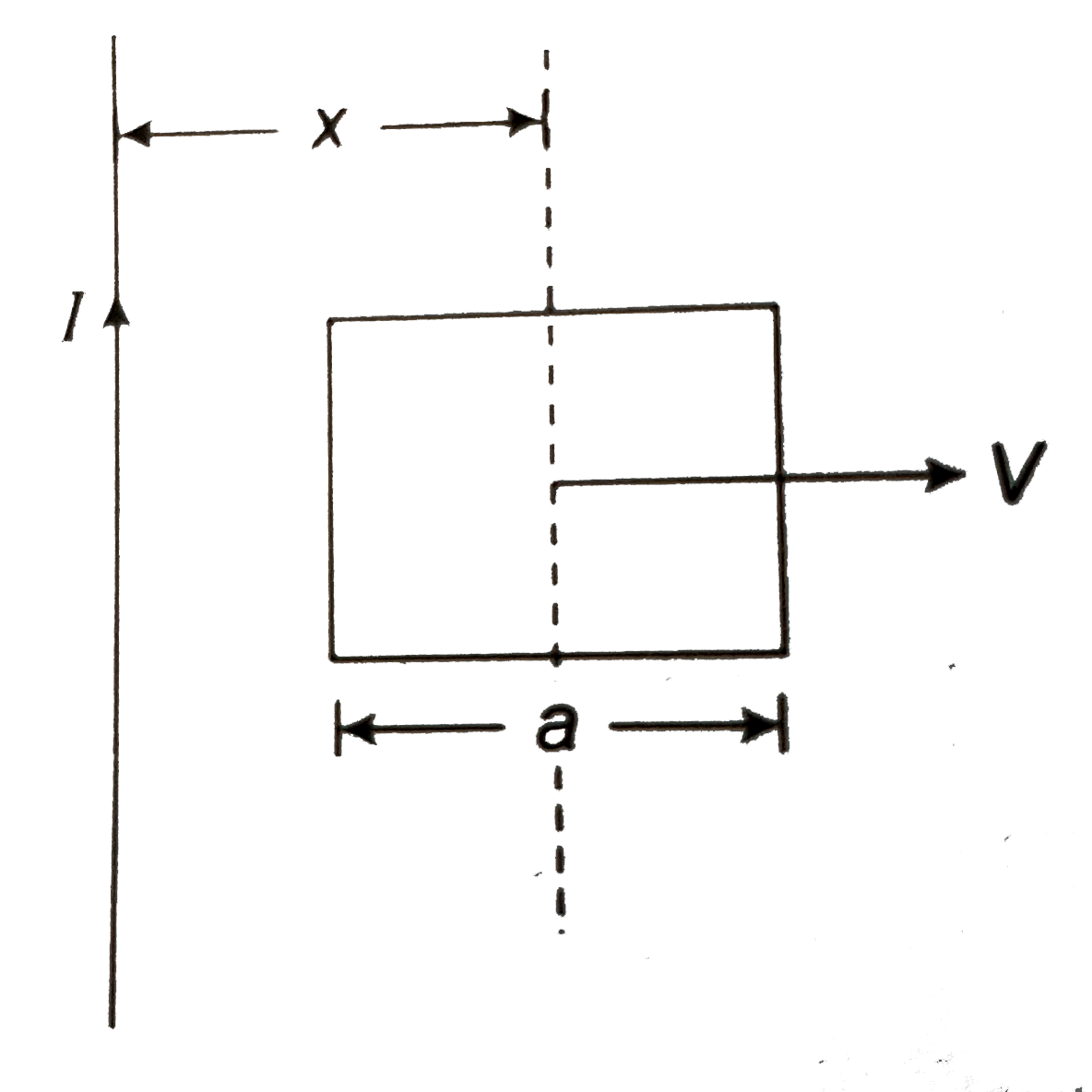
View SolutionA conducting square frame of side 'a' and a long straight wire carrying current I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity 'V'. The emf induced in the frame will be proportional to
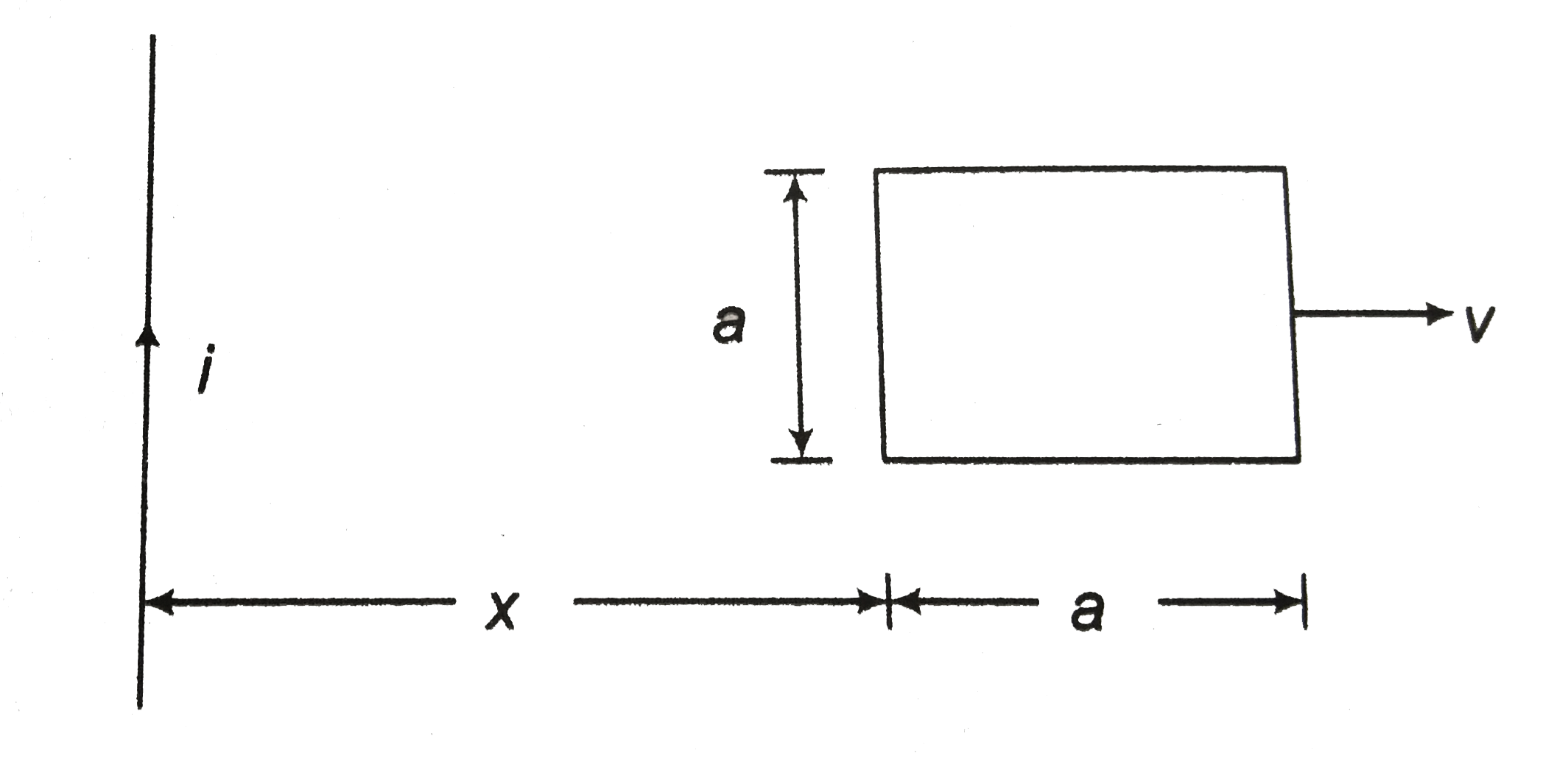
View SolutionA square frame with side a and a long straight wire carrying a current i are located in the same plane as m shown in figure. The fram translates to the right with a constant velocity v. Find the emf induced in the frame as a function of distance x.
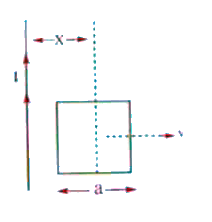
View SolutionA conducting square frame of side .a. and a long straight wire carrying currnet I are located in the same plane as shown in the figure. The frame moves to the right with a constant velocity .V.. The emf induced inthe frame will be proportional to
View Solution
