If θ is the abgle between two vectors A and B , then match the following two columns.
Column I Column II(A)A.B=|A×B|(P)θ=90∘(B)A.B=B2(Q)θ=0∘or180∘(C)|A+B|=|A−C|(r)A=B(D)|A×B|=AB(s)None
The correct Answer is:A→s, B→q,r , C→ p, D→p
To solve the problem of matching the conditions given in Column I with the corresponding statements in Column II, we will analyze each condition step by step.
1. Condition A: A⋅B=|A×B|
- We know that the dot product A⋅B is given by:
A⋅B=|A||B|cosθ
- The magnitude of the cross product |A×B| is given by:
|A×B|=|A||B|sinθ
- Setting these two equal gives:
|A||B|cosθ=|A||B|sinθ
- Dividing both sides by |A||B| (assuming |A|,|B|≠0):
cosθ=sinθ
- This implies:
tanθ=1⟹θ=45∘
- Since there is no option for 45∘ in Column II, we match A to (s) "None".
2. Condition B: A⋅B=B2
- The dot product can be expressed as:
A⋅B=|A||B|cosθ
- The right side, B2, is:
B2=|B|⋅|B|=|B|2
- Setting these equal gives:
|A||B|cosθ=|B|2
- Dividing both sides by |B| (assuming |B|≠0):
|A|cosθ=|B|
- This can only hold true if cosθ=1 (which implies θ=0∘) and |A|=|B|. However, since there is no option for this specific case in Column II, we match B to (s) "None".
3. Condition C: |A+B|=|A−C|
- We start with the equation:
|A+B|2=|A−C|2
- Expanding both sides:
|A|2+|B|2+2A⋅B=|A|2+|C|2−2A⋅C
- Canceling |A|2 from both sides:
|B|2+2A⋅B=|C|2−2A⋅C
- This condition can hold true when θ=90∘ (as the terms involving A⋅B and A⋅C would cancel out). Thus, we match C to (P) θ=90∘.
4. Condition D: |A×B|=AB
- The magnitude of the cross product is:
|A×B|=|A||B|sinθ
- Setting this equal to AB:
|A||B|sinθ=|A||B|
- Dividing both sides by |A||B| (assuming |A|,|B|≠0):
sinθ=1
- This occurs when θ=90∘. Thus, we match D to (P) θ=90∘.
Final Matching:
- A → (s) "None"
- B → (s) "None"
- C → (P) θ=90∘
- D → (P) θ=90∘
Summary of Matches:
- A → s
- B → s
- C → P
- D → P
- We know that the dot product A⋅B is given by:
A⋅B=|A||B|cosθ
- The magnitude of the cross product |A×B| is given by:
|A×B|=|A||B|sinθ
- Setting these two equal gives:
|A||B|cosθ=|A||B|sinθ
- Dividing both sides by |A||B| (assuming |A|,|B|≠0):
cosθ=sinθ
- This implies:
tanθ=1⟹θ=45∘
- Since there is no option for 45∘ in Column II, we match A to (s) "None".
- The dot product can be expressed as:
A⋅B=|A||B|cosθ
- The right side, B2, is:
B2=|B|⋅|B|=|B|2
- Setting these equal gives:
|A||B|cosθ=|B|2
- Dividing both sides by |B| (assuming |B|≠0):
|A|cosθ=|B|
- This can only hold true if cosθ=1 (which implies θ=0∘) and |A|=|B|. However, since there is no option for this specific case in Column II, we match B to (s) "None".
- We start with the equation:
|A+B|2=|A−C|2
- Expanding both sides:
|A|2+|B|2+2A⋅B=|A|2+|C|2−2A⋅C
- Canceling |A|2 from both sides:
|B|2+2A⋅B=|C|2−2A⋅C
- This condition can hold true when θ=90∘ (as the terms involving A⋅B and A⋅C would cancel out). Thus, we match C to (P) θ=90∘.
- The magnitude of the cross product is:
|A×B|=|A||B|sinθ
- Setting this equal to AB:
|A||B|sinθ=|A||B|
- Dividing both sides by |A||B| (assuming |A|,|B|≠0):
sinθ=1
- This occurs when θ=90∘. Thus, we match D to (P) θ=90∘.
- A → (s) "None"
- B → (s) "None"
- C → (P) θ=90∘
- D → (P) θ=90∘
- A → s
- B → s
- C → P
- D → P
Topper's Solved these Questions
Similar Questions
Two vector A and B have rqual magnitude x .Angle between tjem is 60∘ Then match the following two columns.
Column I Column II(A)|A+B|(P)√32x2(B)|A−B|(Q)x(C)A.B(r)√3x(D)|A×B|(s)None
View SolutionVector A is pointing eastwards and vector B northwards .If |A|=|B| then match the following two columns.
Column I Column II(A)(A+B)(P)north -east(B)(A−B)(Q)Vertically upwards(C)(A×B)(r)south-east(D)(A×B)×(A×B)(s)None
View Solution
Knowledge Check
Match the Column I and Column II.,B
 AA-p, B-q, C-r, D-sBA-q, B-r, C-s. D-pCA-r, B-q, C-p, D-pDA-r, B-s, C-p, D-q
AA-p, B-q, C-r, D-sBA-q, B-r, C-s. D-pCA-r, B-q, C-p, D-pDA-r, B-s, C-p, D-q
A vector has a magnitude x . If it is rotated by an angle θ then magnitude of change in vector is nx. Match the following two columns.
Column I Column II(A)θ=60∘(P)n=√3(B)θ=90∘(Q)n=1(C)θ=120∘(r)n=√2(D)θ=180∘(s)n=2
View SolutionIf A.B=A×B, then angle between A and B is
View SolutionA disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
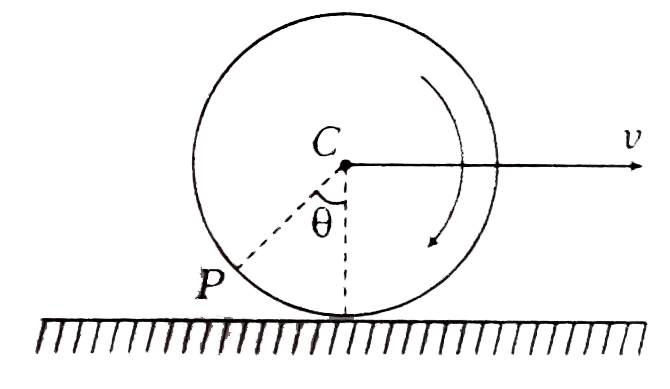
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
View SolutionMatch the following columns.
Column IColumn IIA.Teslap[ML2A−2T−2]B.Weberq[MLA−2T−1]C.Weber m−2r.[MA−1T−2]D.Henrys.None
View SolutionThe angle between two vector A and B is θ. Vector R is the resultant of the two vectors. If R makes an angle θ2 with A, then
View SolutionMatch the following
Column-IColumn-II(A)Enthalpy(p)Extensive property(B)Entropy(q)H - TS(C)Free energy(r)E + PV(D)Pressure(s)Intensive property
View SolutionColumn IColumn II(A)R/L(p)Time(B)C/R(q)Frequency(C)E/B(r)Speed(D)√ε0μ0(s)None
View Solution
