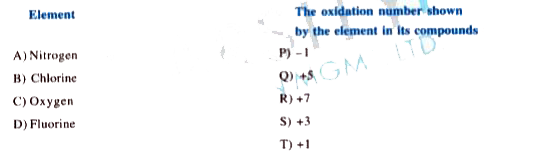Match the following columns.
Column IColumn IIA.Teslap[ML2A−2T−2]B.Weberq[MLA−2T−1]C.Weber m−2r.[MA−1T−2]D.Henrys.None
The correct Answer is:(A→r;B→s;C→r;D→p)
To solve the problem of matching the units in Column I with their corresponding dimensions in Column II, we will analyze each unit one by one.
1. Match Tesla (A):
- Tesla (T) is the unit of magnetic field.
- The formula for the magnetic field (B) is given by:
B=FQ⋅V
- Where:
- F (force) has dimensions (M1L1T−2)
- Q (charge) is I⋅T (current times time), so its dimensions are (A1T1)
- V (velocity) has dimensions (L1T−1)
- Substituting these into the formula:
B=(M1L1T−2)(A1T1)⋅(L1T−1)=(M1L1T−2)(A1L1T0)=(M1A−1T−2)
- Therefore, Tesla corresponds to R: (M1A−1T−2).
2. Match Weber (B):
- Weber (Wb) is the unit of magnetic flux.
- The magnetic flux (Φ) is given by:
Φ=B⋅A
- Where:
- B has dimensions (M1A−1T−2) (as calculated above)
- A (area) has dimensions (L2)
- Thus, the dimensions for magnetic flux are:
Φ=(M1A−1T−2)⋅(L2)=(M1L2A−1T−2)
- This matches with S: "None" since there is no corresponding match in Column II.
3. Match Weber m−2 (C):
- Weber per square meter (Wb/m²) is equivalent to Tesla (T).
- Therefore, the dimensions are the same as those for Tesla:
(M1A−1T−2)
- Thus, Weber per square meter also corresponds to R.
4. Match Henry (D):
- Henry (H) is the unit of inductance.
- The inductance (L) is given by:
L=ΦI
- Where:
- Φ has dimensions (M1L2A−1T−2) (as calculated for Weber)
- I (current) has dimensions (A1)
- Therefore, the dimensions for inductance are:
L=(M1L2A−1T−2)(A1)=(M1L2A−2T−2)
- This matches with P: (M1L2A−2T−2).
Final Matches:
- A (Tesla) → R (M1A−1T−2)
- B (Weber) → S (None)
- C (Weber m−2) → R (M1A−1T−2)
- D (Henry) → P (M1L2A−2T−2)
- Tesla (T) is the unit of magnetic field.
- The formula for the magnetic field (B) is given by:
B=FQ⋅V
- Where:
- F (force) has dimensions (M1L1T−2)
- Q (charge) is I⋅T (current times time), so its dimensions are (A1T1)
- V (velocity) has dimensions (L1T−1)
- Substituting these into the formula:
B=(M1L1T−2)(A1T1)⋅(L1T−1)=(M1L1T−2)(A1L1T0)=(M1A−1T−2)
- Therefore, Tesla corresponds to R: (M1A−1T−2).
- Weber (Wb) is the unit of magnetic flux.
- The magnetic flux (Φ) is given by:
Φ=B⋅A
- Where:
- B has dimensions (M1A−1T−2) (as calculated above)
- A (area) has dimensions (L2)
- Thus, the dimensions for magnetic flux are:
Φ=(M1A−1T−2)⋅(L2)=(M1L2A−1T−2)
- This matches with S: "None" since there is no corresponding match in Column II.
- Weber per square meter (Wb/m²) is equivalent to Tesla (T).
- Therefore, the dimensions are the same as those for Tesla:
(M1A−1T−2)
- Thus, Weber per square meter also corresponds to R.
- Henry (H) is the unit of inductance.
- The inductance (L) is given by:
L=ΦI
- Where:
- Φ has dimensions (M1L2A−1T−2) (as calculated for Weber)
- I (current) has dimensions (A1)
- Therefore, the dimensions for inductance are:
L=(M1L2A−1T−2)(A1)=(M1L2A−2T−2)
- This matches with P: (M1L2A−2T−2).
- A (Tesla) → R (M1A−1T−2)
- B (Weber) → S (None)
- C (Weber m−2) → R (M1A−1T−2)
- D (Henry) → P (M1L2A−2T−2)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery25videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions17videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
Column A1<p<3ColumnBp22p
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
Match the column (1) with column (2)
 View Solution
View SolutionFour rods of equal length l and mass m each forms a square as shown in figure
Moment of inertia about three axes 1,2 and 3 are say I1,I2andI3. Then, match the following columns

Column-IColumn-II(A)I1(p)43ml2(B)I2(q)23ml2(C)I3(r)12ml2(s)NoneView SolutionMatch the column I w.r.t column II
 View Solution
View SolutionMatch the following columns,
Column1Column2a Thermal resitancep [MT^(-3)K^(-4)]b Stefan's constantq [M^(-1)L^(-2)T^(3)K]c Wien's constantr [ML^(2)T^(-3)]d Heat currents [LK]View SolutionColumn IColumn II(A)Work(p)[A1/2T−1](B)Moment of inertia(q)[FA1/2](C)Velocity(r)[FA1/2T2]
View SolutionMatch the following
Table-1Table-2(A)L(P)[M0L0T−2](B)Magnetic Flux(Q)[ML2T−2A−1](C)LC(R)[ML2T−2A−2](D)CR2(S)NoneView SolutionIn the circuit shown in figure, E = 10 V, r = 1Ω,
R = 4Ω and L = 5H. The circuit is closed at time t = 0.
Then, match the following two columns.
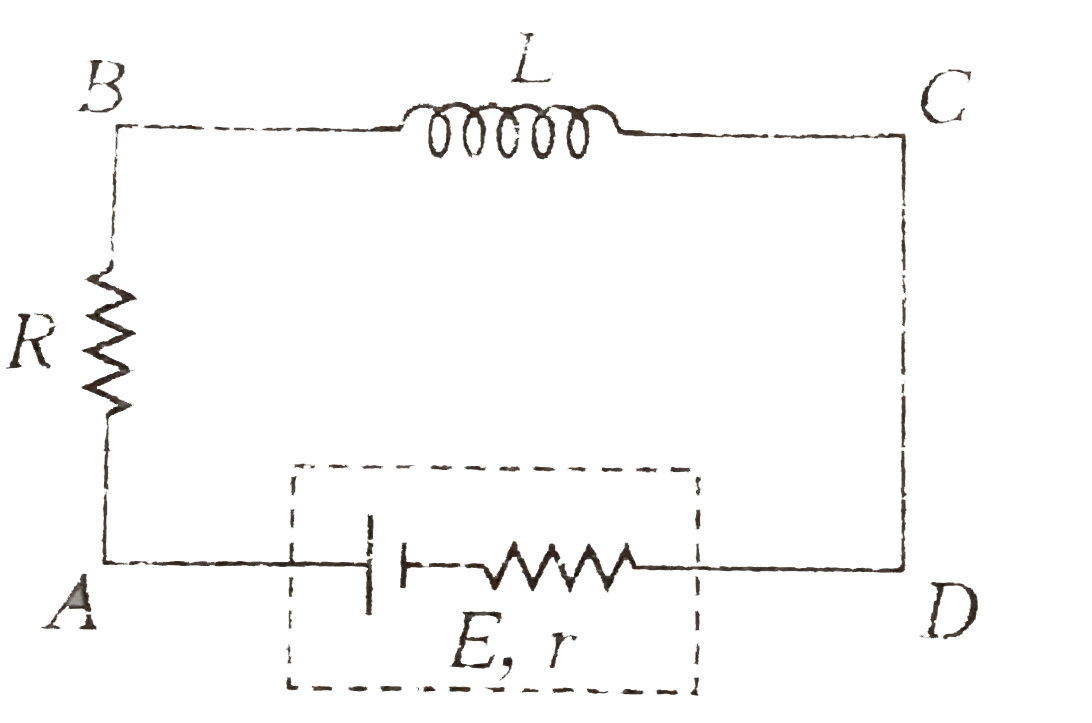
Column IColumn IIA.VAD at t = 0p4VB.VBC at t = 0q8VC.VAB at t =∞r.0VD.VAD at t=∞s.10VView Solution