If $θ_{1}$ and $θ_{2}$ be the apparent angles of dip observed in two verticle planes at right angles to each other, then the true angle of dip $θ$ is given by

A

${cot}^{2} θ = {cot}^{2} θ_{1} + {cot}^{2} θ_{2}$

B

${tan}^{2} θ = {tan}^{2} θ_{1} + {tan}^{2} θ_{2}$

C

${cot}^{2} θ = {cot}^{2} θ_{1} - {cot}^{2} θ_{2}$

D

${tan}^{2} θ = {tan}^{2} θ_{1} - {tan}^{2} θ_{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let the $B_{H} and B_{V}$ be the horizontal and vertical component of earth 's magnetic field B.
$tan θ = \frac{B_{V}}{B_{H}} \Rightarrow cot θ = \frac{B_{H}}{B_{V}}$

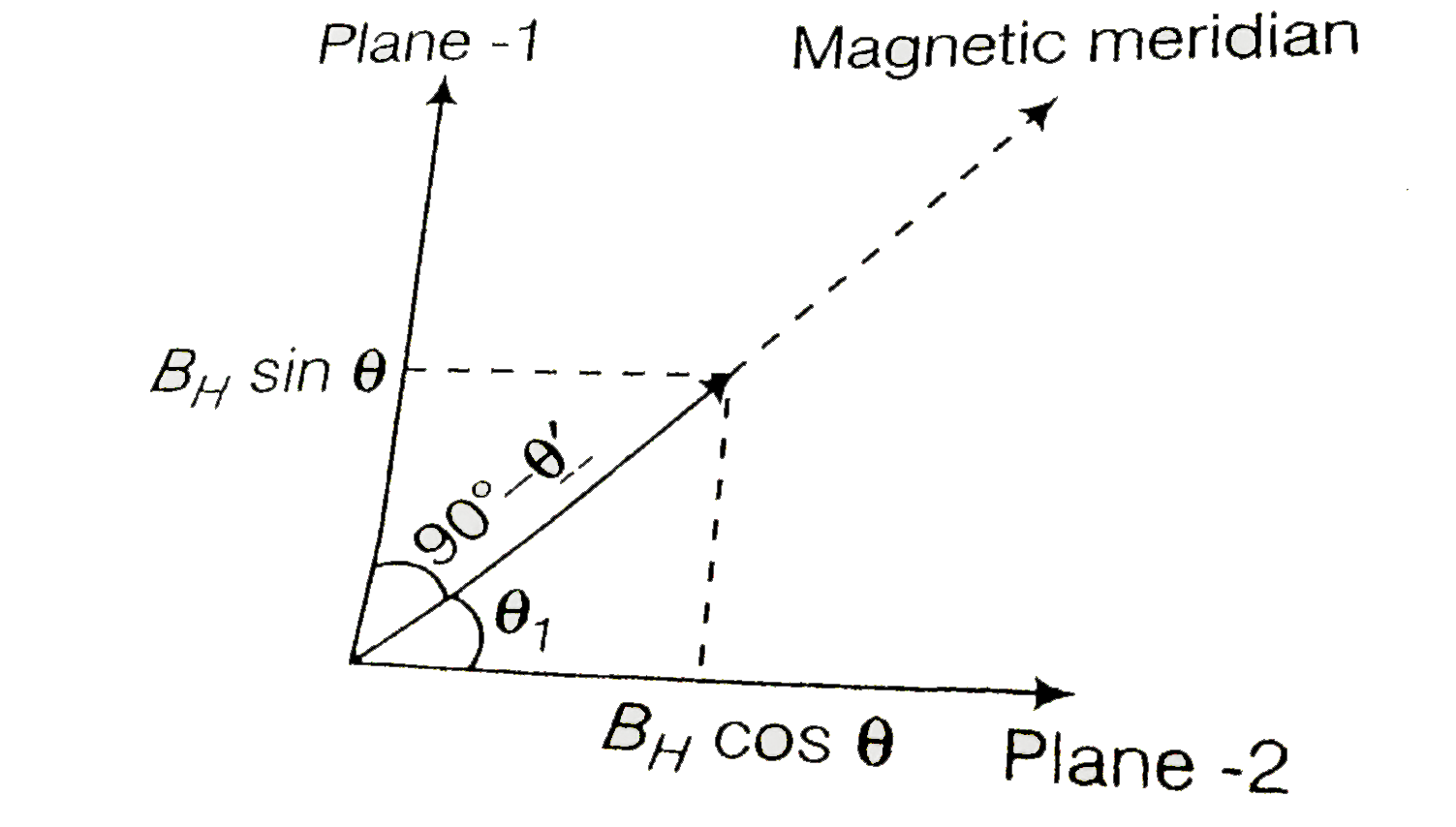
Let plane 1 and 2 are mutually perpendicular planes making angle $θ and (90^{\circ} - θ)$ with magnetic meridian.The vertical component of earth of earth's magnetic field remain same in two plane but effective horizontal component in the two planes is given by
$B_{1} = B_{H} cos θ$
and " " $B_{2} = B_{H} sin θ$
Then , ${tan θ}_{1} = \frac{B_{V}}{B_{1}} = \frac{B_{V}}{B_{H} cos θ'} \Rightarrow {cot θ}_{1} = \frac{B_{H} cos θ'}{B_{V}}$
Similarly,
$\Rightarrow {tan θ}_{2} = \frac{B_{V}}{B_{1}} = \frac{B_{V}}{B_{H} sin θ' \Rightarrow {cot θ}_{2} = (B_{H} sin θ) \frac{'}{B_{V}}}$
From Eq (iv) and Eq (v)
$\Rightarrow {cot}^{2} θ_{1} + {cot}^{2} θ_{2} = \frac{B_{H}^{2} {cos}^{2} θ}{B_{V}^{2}} + \frac{B_{H}^{2} {sin}^{2} θ}{B_{V}^{2}}$
${cot}^{2} θ_{1} + {cot}^{2} θ_{2} = \frac{B_{H}^{2}}{B_{V}^{2}} {cos}^{2} θ + {sin}^{2 θ}$
$\Rightarrow {cot}^{2} θ_{1} + {cot}^{2} θ_{2} = {cot}^{2} θ$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

DC PANDEY ENGLISH-SOLVED PAPER 2017-Solved papers 2017(JIPMER)

Home
Ask Doubt
Profile