If →A,→B,→C represents the three sides of an equilateral triangle taken in the same order then find the angle between (i) →Aand→B(ii)→Band→C(iii)Aand→C.
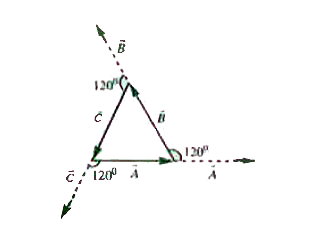
From the diagram the angle between the vectors →Aand→B is 120∘ the angle between →Band→C is 120∘ the angle between →Aand→C is 120∘
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Vectors & Scalars)
25 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - EXERCISE-A (Addition & Subtractions of Vectors)
10 Videos
- MAGNETISMBOOK - AAKASH SERIESCHAPTER - MAGNETISMEXERCISE - ADDITIONAL EXERCISE
22 Videos
- MOTION IN A PLANEBOOK - AAKASH SERIESCHAPTER - MOTION IN A PLANEEXERCISE - QUESTION FOR DESCRIPTIVE ANSWER
7 Videos
Similar Questions
Three vectors →A,→B,→C are shown in the figure angle between (i) →Aand→B(ii)→Band→C,(iii)→Aand→C

View SolutionIf |→a|+∣∣→b∣∣=|→c|and→a+→b=→c then find the angle between →aand→b.
View Solutionif →a,→band→c are mutally perpendicular vectors of equal magnitudes, then find the angle between vectors and →a+→b+→c.
View SolutionIf →a+→b+→c=0,|→a|=3,∣∣→b∣∣=5,|→c|=7 , then find the angle between →aand→b.
View SolutionIf →a+→b+→c=0,|→a|=3,∣∣→b∣∣=5,|→c|=7 , then find the angle between →aand→b.
View SolutionIf →a+→b+→c=0,|→a|=3,∣∣→b∣∣=5,|→c|=7 , then find the angle between →aand→b.
View SolutionIf three unit vectors →a,→band→c satisfy→a+→b+→c=→0. Then find the angle between →aand→b.
View SolutionLet →a,→b,→c be three unit vectors and →a.→b=→a.→c=0 . If the angle between →band→c is π3 then find the value of ∣∣[→a→b→c]∣∣
View SolutionIf →a,→b,→c are unit vectors such that →a.→b=0=→a.→c and the angle between →band→cisπ3 , then find the value of ∣∣→a×→b−→a×→c∣∣
View SolutionThree vectors →A,→B and →C are such that →A=→B+→C and their magnitudes are in ratio 5:4:3 respectively. Find angle between vector →A and →C
View Solution
